ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
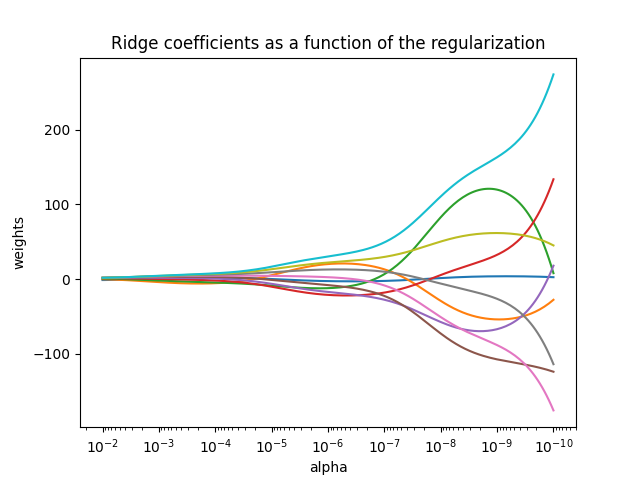
رسم معاملات Ridge كدالة للتنظيم#
يظهر هذا المثال تأثير التلازم في معاملات أداة التقدير.
Ridge الانحدار هو أداة التقدير المستخدمة في هذا المثال.
يمثل كل لون ميزة مختلفة في
متجه المعاملات، ويتم عرضه كدالة ل
معامل التنظيم.
يوضح هذا المثال أيضًا فائدة تطبيق الانحدار Ridge على المصفوفات ذات الشرط السيئ للغاية. بالنسبة لهذه المصفوفات، يمكن أن يسبب التغيير الطفيف في المتغير المستهدف تباينات كبيرة في الأوزان المحسوبة. في مثل هذه الحالات، من المفيد تعيين بعض التنظيم (alpha) للحد من هذا التباين (الضوضاء).
عندما يكون alpha كبيرًا جدًا، تهيمن تأثيرات التنظيم على دالة الخسارة التربيعية وتميل المعاملات إلى الصفر. في نهاية المسار، عندما يقترب alpha من الصفر وتميل الحلول نحو المربعات العادية الأقل، تظهر المعاملات تذبذبات كبيرة. في الممارسة العملية، من الضروري ضبط alpha بطريقة تحافظ على التوازن بين الاثنين.
# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
# X هي مصفوفة هيلبرت 10x10
X = 1.0 / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
حساب المسارات#
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_)
عرض النتائج#
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # عكس المحور
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge coefficients as a function of the regularization")
plt.axis("tight")
plt.show()
Total running time of the script: (0 minutes 0.430 seconds)
Related examples
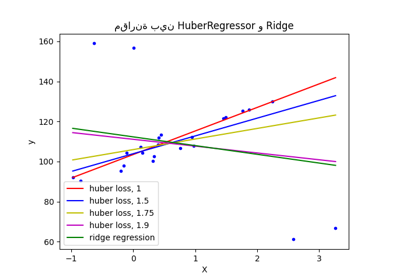
مقارنة بين HuberRegressor و Ridge على مجموعة بيانات تحتوي على قيم شاذة قوية
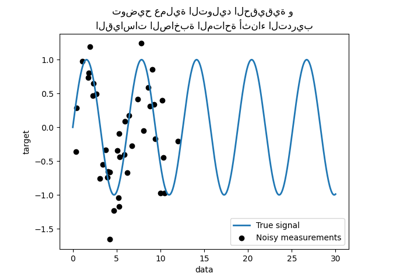
مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية