ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

انحدار ثيل-سين#

يحسب انحدار ثيل-سين على مجموعة بيانات اصطناعية.

راجع مُقدِّر Theil-Sen: مُقدِّر قائم على الوسيط المُعمم لمزيد من المعلومات حول المنحدر.

بالمقارنة مع مقدر المربعات الصغرى العادي (OLS)، فإن مقدر ثيل-سين قوي ضد القيم الشاذة. لديه نقطة انهيار حوالي 29.3% في حالة الانحدار الخطي البسيط، مما يعني أنه يمكنه تحمل البيانات الفاسدة (القيم الشاذة) بنسبة تصل إلى 29.3% في الحالة ثنائية الأبعاد.

يتم تقدير النموذج عن طريق حساب المنحدرات والتقاطعات للسكان الفرعيين لجميع التركيبات الممكنة من النقاط الفرعية p. إذا كان تم تركيب التقاطع، يجب أن يكون p أكبر من أو يساوي n_features + 1. ثم يتم تعريف المنحدر والتقاطع النهائيين كمتوسط مكاني لهذه المنحدرات والتقاطعات.

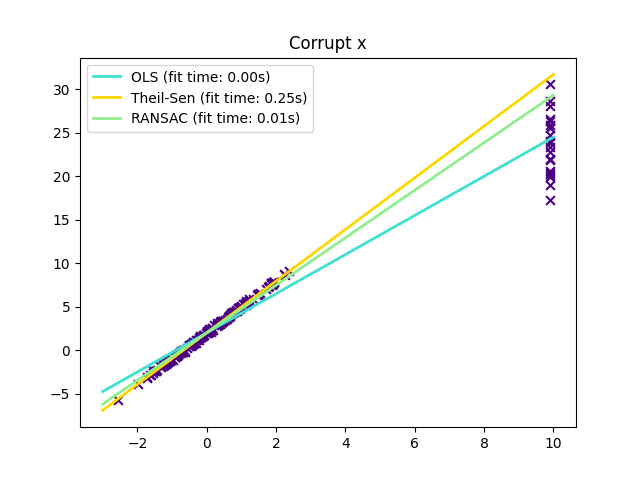
في بعض الحالات، يؤدي ثيل-سين أداءً أفضل من RANSAC، وهي طريقة قوية أيضًا. يتم توضيح ذلك في المثال الثاني أدناه حيث تؤثر القيم الشاذة فيما يتعلق بمحور x على RANSAC. يصلح ضبط معلمة "residual_threshold" في RANSAC هذا الأمر، ولكن بشكل عام، هناك حاجة إلى معرفة مسبقة حول البيانات وطبيعة القيم الشاذة. بسبب التعقيد الحسابي لثيل-سين، يوصى باستخدامه فقط للمشاكل الصغيرة من حيث عدد العينات والميزات. بالنسبة للمشاكل الأكبر تقيد معلمة "max_subpopulation" حجم جميع التركيبات الممكنة من النقاط الفرعية p إلى مجموعة فرعية يتم اختيارها عشوائيًا وبالتالي تحد أيضًا من وقت التشغيل. لذلك، يمكن تطبيق ثيل-سين على مشاكل أكبر مع عيب فقدان بعض خصائصه الرياضية حيث أنه يعمل على مجموعة فرعية عشوائية.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression, RANSACRegressor, TheilSenRegressor

estimators = [
    ("OLS", LinearRegression()),
    ("Theil-Sen", TheilSenRegressor(random_state=42)),
    ("RANSAC", RANSACRegressor(random_state=42)),
]
colors = {"OLS": "turquoise", "Theil-Sen": "gold", "RANSAC": "lightgreen"}
lw = 2

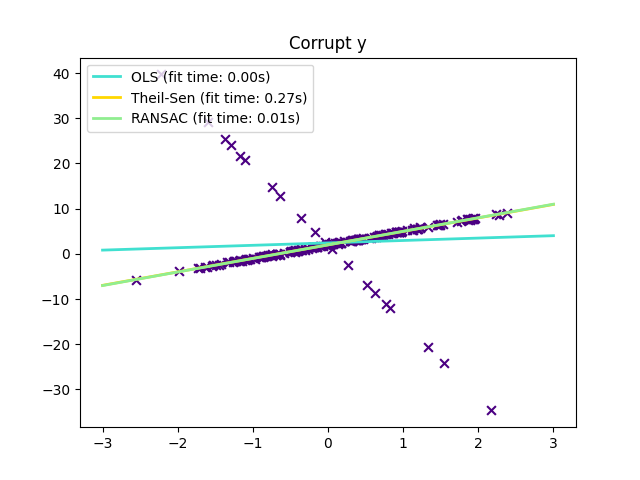
القيم الشاذة فقط في اتجاه y#

np.random.seed(0)
n_samples = 200
# النموذج الخطي y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
w = 3.0
c = 2.0
noise = 0.1 * np.random.randn(n_samples)
y = w * x + c + noise
# 10% قيم شاذة
y[-20:] += -20 * x[-20:]
X = x[:, np.newaxis]

plt.scatter(x, y, color="indigo", marker="x", s=40)
line_x = np.array([-3, 3])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
_ = plt.title("Corrupt y")

القيم الشاذة في اتجاه X#

np.random.seed(0)
# النموذج الخطي y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
noise = 0.1 * np.random.randn(n_samples)
y = 3 * x + 2 + noise
# 10% قيم شاذة
x[-20:] = 9.9
y[-20:] += 22
X = x[:, np.newaxis]

plt.figure()
plt.scatter(x, y, color="indigo", marker="x", s=40)

line_x = np.array([-3, 10])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
plt.title("Corrupt x")
plt.show()