ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
المزالق الشائعة في تفسير معاملات النماذج الخطية#
في النماذج الخطية، يتم نمذجة القيمة المستهدفة كمجموعة خطية من الميزات (انظر قسم النماذج الخطية في دليل المستخدم لوصف مجموعة من النماذج الخطية المتاحة في scikit-learn). تمثل المعاملات في النماذج الخطية المتعددة العلاقة بين الميزة المعينة، \(X_i\) والهدف، \(y\)، بافتراض أن جميع الميزات الأخرى تظل ثابتة ( التبعية الشرطية). هذا يختلف عن رسم \(X_i\) مقابل \(y\) وملاءمة علاقة خطية: في هذه الحالة، تؤخذ جميع القيم الممكنة للميزات الأخرى في الاعتبار في التقدير (التبعية الهامشية).
سيقدم هذا المثال بعض التلميحات في تفسير المعامل في النماذج الخطية، مشيرًا إلى المشاكل التي تنشأ عندما يكون النموذج الخطي غير مناسب لوصف مجموعة البيانات، أو عندما تكون الميزات مترابطة.
ملاحظة
ضع في اعتبارك أن الميزات \(X\) والنتيجة \(y\) هي بشكل عام نتيجة عملية توليد بيانات غير معروفة لنا. يتم تدريب نماذج التعلم الآلي لتقريب الدالة الرياضية غير المرصودة التي تربط \(X\) بـ \(y\) من بيانات العينة. نتيجة لذلك، قد لا يعمم أي تفسير يتم إجراؤه حول نموذج ما بالضرورة على عملية توليد البيانات الحقيقية. هذا صحيح بشكل خاص عندما يكون النموذج ذو جودة سيئة أو عندما لا تكون بيانات العينة ممثلة للسكان.
سنستخدم بيانات من "مسح السكان الحالي" من عام 1985 للتنبؤ بالأجور كدالة لميزات مختلفة مثل الخبرة والعمر أو التعليم.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
مجموعة البيانات: الأجور#
نحصل على البيانات من OpenML.
لاحظ أن تعيين المعلمة as_frame إلى True سيسترجع البيانات
كإطار بيانات pandas.
from sklearn.datasets import fetch_openml
survey = fetch_openml(data_id=534, as_frame=True)
بعد ذلك، نحدد الميزات X والأهداف y: العمود WAGE هو متغيرنا
المستهدف (أي المتغير الذي نريد التنبؤ به).
X = survey.data[survey.feature_names]
X.describe(include="all")
لاحظ أن مجموعة البيانات تحتوي على متغيرات فئوية ورقمية. سنحتاج إلى مراعاة ذلك عند معالجة مجموعة البيانات مسبقًا فيما بعد.
X.head()
هدفنا للتنبؤ: الأجر. يتم وصف الأجور كرقم فاصلة عائمة بالدولار في الساعة.
y = survey.target.values.ravel()
survey.target.head()
0 5.10
1 4.95
2 6.67
3 4.00
4 7.50
Name: WAGE, dtype: float64
نقسم العينة إلى مجموعة بيانات تدريب ومجموعة بيانات اختبار. سيتم استخدام مجموعة بيانات التدريب فقط في التحليل الاستكشافي التالي. هذه طريقة لمحاكاة موقف حقيقي حيث يتم إجراء التنبؤات على هدف غير معروف، ولا نريد أن يكون تحليلنا وقراراتنا متحيزة بمعرفتنا ببيانات الاختبار.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
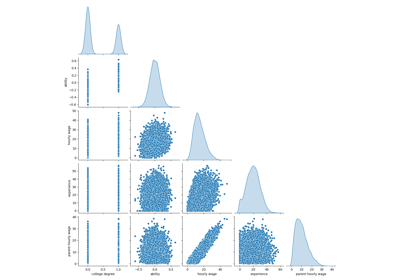
أولاً، دعنا نحصل على بعض الأفكار من خلال النظر إلى توزيعات المتغيرات و في العلاقات الزوجية بينها. سيتم استخدام المتغيرات الرقمية فقط. في الرسم التخطيطي التالي، تمثل كل نقطة عينة.
train_dataset = X_train.copy()
train_dataset.insert(0, "WAGE", y_train)
_ = sns.pairplot(train_dataset, kind="reg", diag_kind="kde")
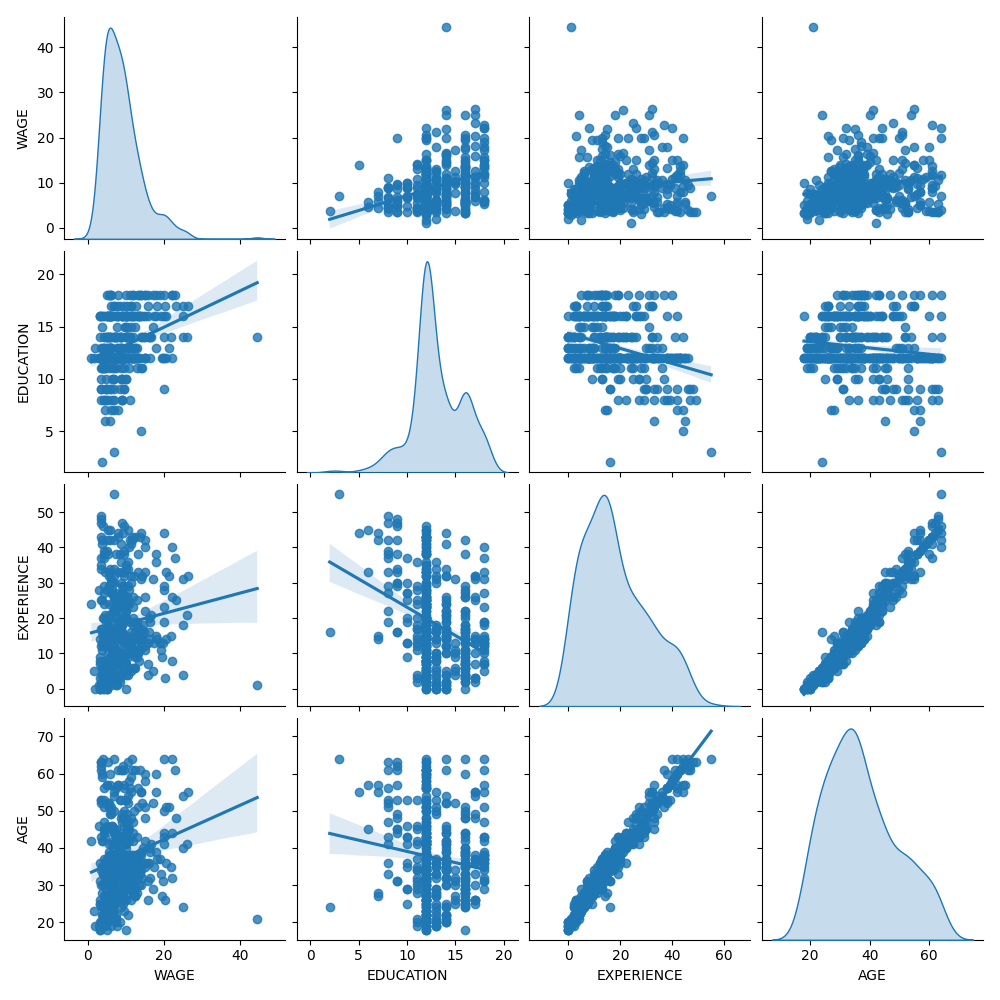
يكشف النظر عن كثب إلى توزيع WAGE أنه يحتوي على ذيل طويل. لهذا السبب، يجب أن نأخذ لوغاريتمه لتحويله تقريبًا إلى توزيع طبيعي (تعمل النماذج الخطية مثل ridge أو lasso بشكل أفضل لتوزيع طبيعي للخطأ).
يزداد WAGE عندما يزداد EDUCATION. لاحظ أن التبعية بين WAGE و EDUCATION الممثلة هنا هي تبعية هامشية، أي أنها تصف سلوك متغير معين دون إبقاء المتغيرات الأخرى ثابتة.
أيضًا، يرتبط EXPERIENCE و AGE ارتباطًا خطيًا قويًا.
خط أنابيب التعلم الآلي#
لتصميم خط أنابيب التعلم الآلي لدينا، نقوم أولاً يدويًا بالتحقق من نوع البيانات التي نتعامل معها:
survey.data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 534 entries, 0 to 533
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 EDUCATION 534 non-null int64
1 SOUTH 534 non-null category
2 SEX 534 non-null category
3 EXPERIENCE 534 non-null int64
4 UNION 534 non-null category
5 AGE 534 non-null int64
6 RACE 534 non-null category
7 OCCUPATION 534 non-null category
8 SECTOR 534 non-null category
9 MARR 534 non-null category
dtypes: category(7), int64(3)
memory usage: 17.2 KB
كما رأينا سابقًا، تحتوي مجموعة البيانات على أعمدة بأنواع بيانات مختلفة ونحتاج إلى تطبيق معالجة مسبقة محددة لكل نوع بيانات. على وجه الخصوص، لا يمكن تضمين المتغيرات الفئوية في النموذج الخطي إذا لم تكن مشفرة كأعداد صحيحة أولاً. بالإضافة إلى ذلك، لتجنب معاملة الميزات الفئوية كقيم مرتبة، نحتاج إلى تشفيرها بنظام واحد ساخن. المعالج المسبق لدينا سوف
يقوم بتشفير الأعمدة الفئوية بنظام واحد ساخن (أي، إنشاء عمود لكل فئة)، فقط للمتغيرات الفئوية غير الثنائية؛
كنهج أول (سنرى بعد ذلك كيف سيؤثر تطبيع القيم الرقمية على مناقشتنا)، احتفظ بالقيم الرقمية كما هي.
from sklearn.compose import make_column_transformer
from sklearn.preprocessing import OneHotEncoder
categorical_columns = ["RACE", "OCCUPATION", "SECTOR", "MARR", "UNION", "SEX", "SOUTH"]
numerical_columns = ["EDUCATION", "EXPERIENCE", "AGE"]
preprocessor = make_column_transformer(
(OneHotEncoder(drop="if_binary"), categorical_columns),
remainder="passthrough",
verbose_feature_names_out=False, # avoid to prepend the preprocessor names
)
لوصف مجموعة البيانات كنموذج خطي، نستخدم انحدار ريدج بتنظيم صغير جدًا ونمذجة لوغاريتم WAGE.
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
),
)
معالجة مجموعة البيانات#
أولاً، نقوم بملاءمة النموذج.
model.fit(X_train, y_train)
ثم نتحقق من أداء النموذج المحسوب برسم تنبؤاته على مجموعة الاختبار وحساب، على سبيل المثال، متوسط الخطأ المطلق للنموذج.
from sklearn.metrics import PredictionErrorDisplay, median_absolute_error
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
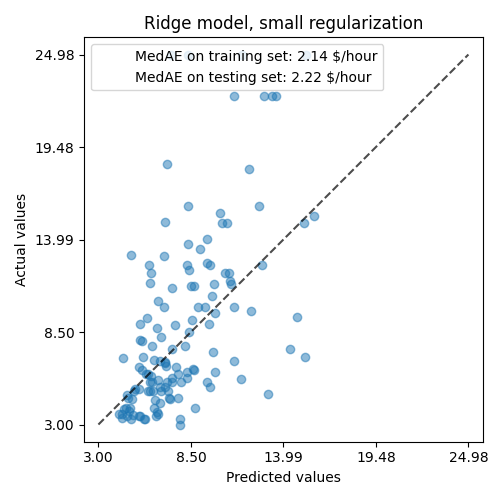
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
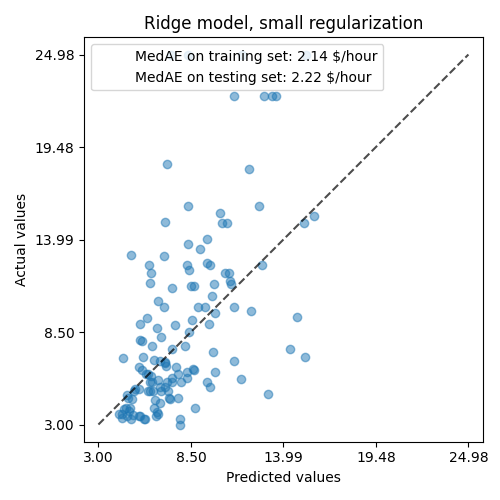
النموذج المتعلم بعيد عن كونه نموذجًا جيدًا يقوم بعمل تنبؤات دقيقة: هذا واضح عند النظر إلى الرسم التخطيطي أعلاه، حيث يجب أن تقع التنبؤات الجيدة على الخط المتقطع الأسود.
في القسم التالي، سوف نفسر معاملات النموذج. أثناء قيامنا بذلك، يجب أن نضع في اعتبارنا أن أي استنتاج نستخلصه هو حول النموذج الذي نبنيه، وليس حول عملية التوليد الحقيقية (العالم الحقيقي) للبيانات.
تفسير المعاملات: المقياس مهم#
بادئ ذي بدء، يمكننا إلقاء نظرة على قيم معاملات الانحدار الذي قمنا بملاءمته.
feature_names = model[:-1].get_feature_names_out()
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients"],
index=feature_names,
)
coefs
يتم التعبير عن معامل AGE بالـ "دولار/ساعة لكل سنة معيشة" بينما يتم التعبير عن معامل EDUCATION بالـ "دولار/ساعة لكل سنة تعليم". هذا التمثيل للمعاملات له فائدة جعل التنبؤات العملية للنموذج واضحة: زيادة بمقدار \(1\) سنة في AGE تعني انخفاضًا بمقدار \(0.030867\) دولار/ساعة، بينما زيادة بمقدار \(1\) سنة في EDUCATION تعني زيادة بمقدار \(0.054699\) دولار/ساعة. من ناحية أخرى، المتغيرات الفئوية (مثل UNION أو SEX) هي أرقام بلا أبعاد تأخذ إما القيمة 0 أو 1. معاملاتها معبر عنها بالدولار/ساعة. بعد ذلك، لا يمكننا مقارنة حجم المعاملات المختلفة لأن الميزات لها مقاييس طبيعية مختلفة، وبالتالي نطاقات قيم مختلفة، بسبب اختلاف وحدات القياس الخاصة بها. هذا أكثر وضوحًا إذا قمنا برسم المعاملات.
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.xlabel("Raw coefficient values")
plt.subplots_adjust(left=0.3)
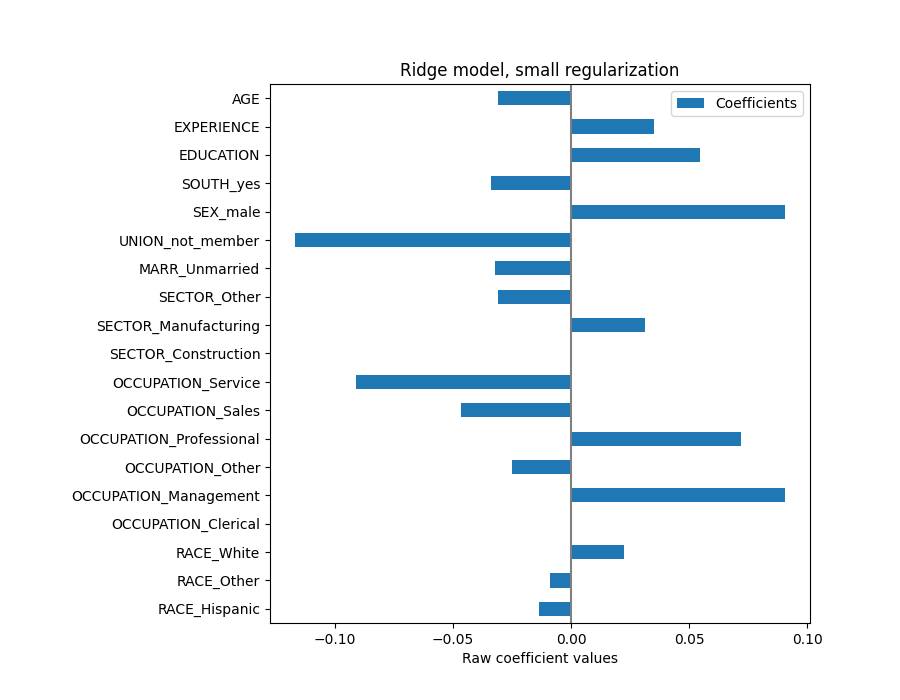
في الواقع، من الرسم البياني أعلاه، يبدو أن العامل الأكثر أهمية في تحديد WAGE هو المتغير UNION، حتى لو أخبرتنا حدسنا أن المتغيرات مثل EXPERIENCE يجب أن يكون لها تأثير أكبر.
قد يكون النظر إلى مخطط المعامل لقياس أهمية الميزة مضللًا حيث يختلف بعضها على نطاق صغير، بينما يختلف البعض الآخر، مثل AGE، أكثر من ذلك بكثير، عدة عقود.
هذا واضح إذا قارنا الانحرافات المعيارية لمختلف الميزات.
X_train_preprocessed = pd.DataFrame(
model[:-1].transform(X_train), columns=feature_names
)
X_train_preprocessed.std(axis=0).plot.barh(figsize=(9, 7))
plt.title("Feature ranges")
plt.xlabel("Std. dev. of feature values")
plt.subplots_adjust(left=0.3)
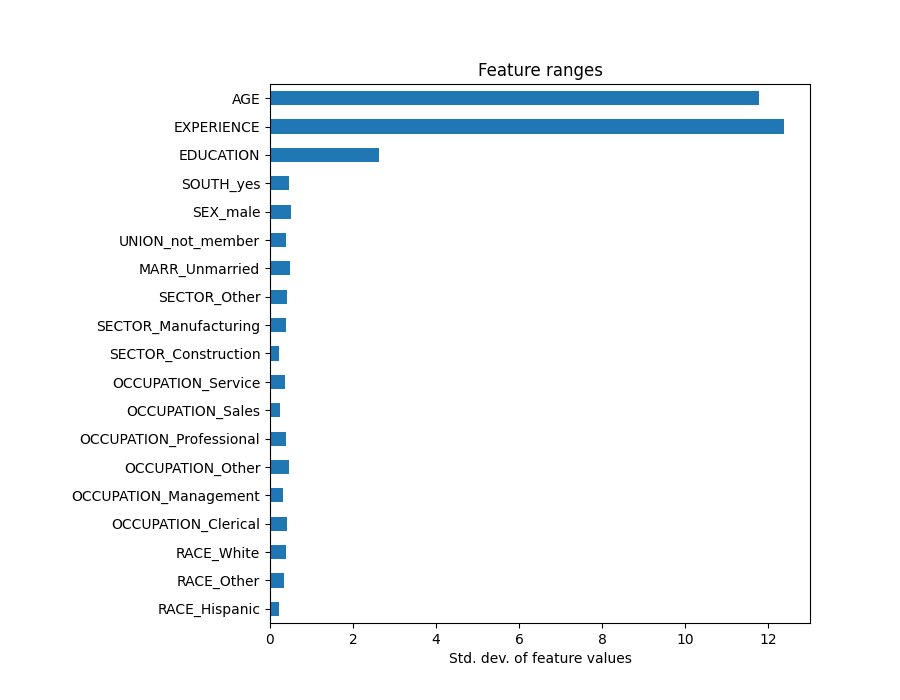
سيؤدي ضرب المعاملات بالانحراف المعياري للميزة ذات الصلة إلى تقليل جميع المعاملات إلى نفس وحدة القياس. كما سنرى لاحقًا هذا يعادل تطبيع المتغيرات الرقمية إلى انحرافها المعياري، مثل \(y = \sum{coef_i \times X_i} = \sum{(coef_i \times std_i) \times (X_i / std_i)}\).
وبهذه الطريقة، نؤكد على أنه كلما زاد تباين الميزة، زاد وزن المعامل المقابل على المخرجات، مع تساوي كل شيء آخر.
coefs = pd.DataFrame(
model[-1].regressor_.coef_ * X_train_preprocessed.std(axis=0),
columns=["Coefficient importance"],
index=feature_names,
)
coefs.plot(kind="barh", figsize=(9, 7))
plt.xlabel("Coefficient values corrected by the feature's std. dev.")
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
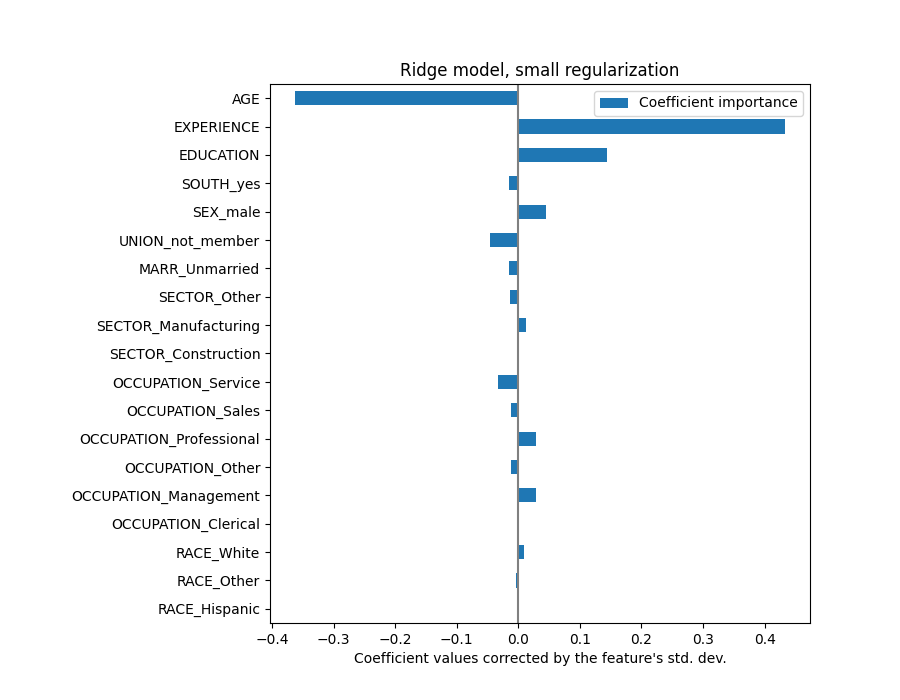
الآن بعد أن تم قياس المعاملات، يمكننا مقارنتها بأمان.
تحذير
لماذا يشير الرسم البياني أعلاه إلى أن الزيادة في العمر تؤدي إلى انخفاض في الأجر؟ لماذا الرسم التخطيطي المزدوج الأولي يخبرنا بالعكس؟
يخبرنا الرسم البياني أعلاه عن التبعيات بين ميزة محددة و الهدف عندما تظل جميع الميزات الأخرى ثابتة، أي التبعيات الشرطية. ستؤدي زيادة AGE إلى انخفاض WAGE عندما تظل جميع الميزات الأخرى ثابتة. على العكس من ذلك، ستؤدي زيادة EXPERIENCE إلى زيادة WAGE عندما تظل جميع الميزات الأخرى ثابتة. أيضًا، AGE و EXPERIENCE و EDUCATION هي المتغيرات الثلاثة التي تؤثر أكثر على النموذج.
تفسير المعاملات: توخي الحذر بشأن السببية#
النماذج الخطية هي أداة رائعة لقياس الارتباط الإحصائي، لكن يجب أن نتوخى الحذر عند إصدار بيانات حول السببية، فبعد كل شيء لا يعني الارتباط دائمًا السببية. هذا صعب بشكل خاص في العلوم الاجتماعية لأن المتغيرات التي نلاحظها تعمل فقط كوكلاء لعملية السببية الأساسية.
في حالتنا الخاصة، يمكننا التفكير في EDUCATION للفرد على أنه وكيل لكفاءته المهنية، وهو المتغير الحقيقي الذي نهتم به ولكن لا يمكننا ملاحظته. نود بالتأكيد أن نعتقد أن البقاء في المدرسة لمدة أطول سيزيد من الكفاءة الفنية، ولكن من الممكن أيضًا تمامًا أن تسير السببية في الاتجاه الآخر أيضًا. أي أن أولئك الذين يتمتعون بكفاءة فنية يميلون إلى البقاء في المدرسة لفترة أطول.
من غير المرجح أن يهتم صاحب العمل بأي حالة هي (أو إذا كانت مزيجًا من الاثنين)، طالما ظل مقتنعًا بأن الشخص الذي لديه المزيد من EDUCATION هو الأنسب للوظيفة، فسيكون سعيدًا بدفع WAGE أعلى.
يصبح هذا الخلط بين الآثار مشكلة عند التفكير في شكل من أشكال التدخل، على سبيل المثال، الإعانات الحكومية للشهادات الجامعية أو المواد الترويجية التي تشجع الأفراد على متابعة التعليم العالي. يمكن أن ينتهي الأمر بالمبالغة في تقدير فائدة هذه التدابير، خاصة إذا كانت درجة الخلط قوية. يتوقع نموذجنا زيادة قدرها \(0.054699\) في الأجر بالساعة لكل سنة تعليم. قد يكون التأثير السببي الفعلي أقل بسبب هذا الخلط.
التحقق من تباين المعاملات#
يمكننا التحقق من تباين المعامل من خلال التحقق المتقاطع: إنه شكل من أشكال اضطراب البيانات (يتعلق بـ إعادة التشكيل).
إذا تغيرت المعاملات بشكل كبير عند تغيير مجموعة بيانات الإدخال، فإن متانتها غير مضمونة، وربما يجب تفسيرها بحذر.
from sklearn.model_selection import RepeatedKFold, cross_validate
cv = RepeatedKFold(n_splits=5, n_repeats=5, random_state=0)
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[
est[-1].regressor_.coef_ * est[:-1].transform(X.iloc[train_idx]).std(axis=0)
for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
],
columns=feature_names,
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.xlabel("Coefficient importance")
plt.title("Coefficient importance and its variability")
plt.suptitle("Ridge model, small regularization")
plt.subplots_adjust(left=0.3)
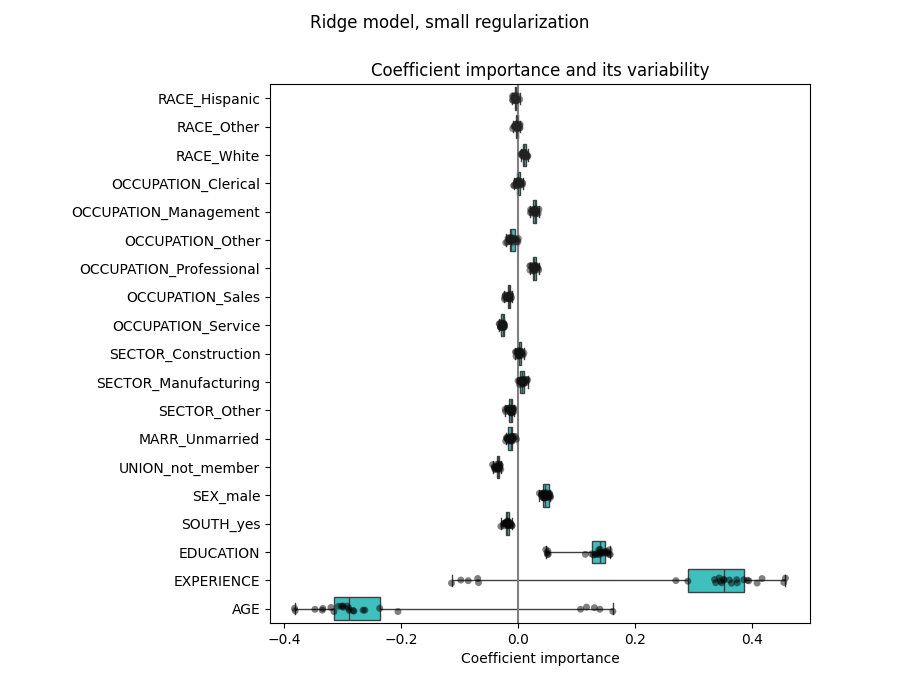
مشكلة المتغيرات المترابطة#
تتأثر معاملات AGE و EXPERIENCE بتباين قوي قد يكون بسبب الترابط الخطي بين الميزتين: نظرًا لأن AGE و EXPERIENCE يختلفان معًا في البيانات، فمن الصعب فصل تأثيرهما.
للتحقق من هذا التفسير، نرسم تباين معامل AGE و EXPERIENCE.
plt.ylabel("Age coefficient")
plt.xlabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")
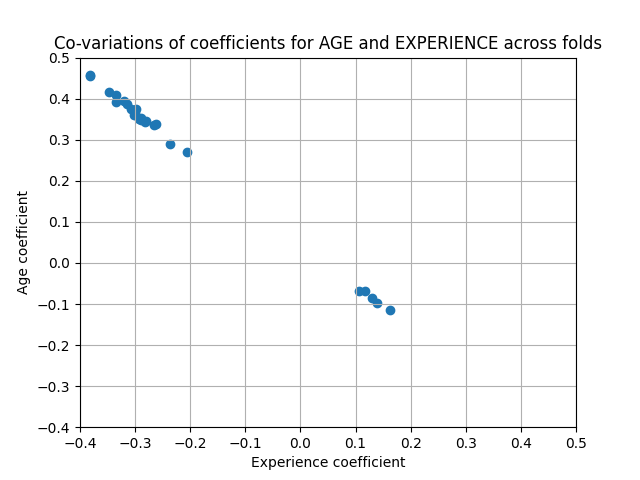
يتم ملء منطقتين: عندما يكون معامل EXPERIENCE موجبًا، يكون معامل AGE سالبًا والعكس صحيح.
للمضي قدمًا، نزيل إحدى الميزتين ونتحقق من تأثير ذلك على استقرار النموذج.
column_to_drop = ["AGE"]
cv_model = cross_validate(
model,
X.drop(columns=column_to_drop),
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[
est[-1].regressor_.coef_
* est[:-1].transform(X.drop(columns=column_to_drop).iloc[train_idx]).std(axis=0)
for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
],
columns=feature_names[:-1],
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5)
plt.axvline(x=0, color=".5")
plt.title("Coefficient importance and its variability")
plt.xlabel("Coefficient importance")
plt.suptitle("Ridge model, small regularization, AGE dropped")
plt.subplots_adjust(left=0.3)
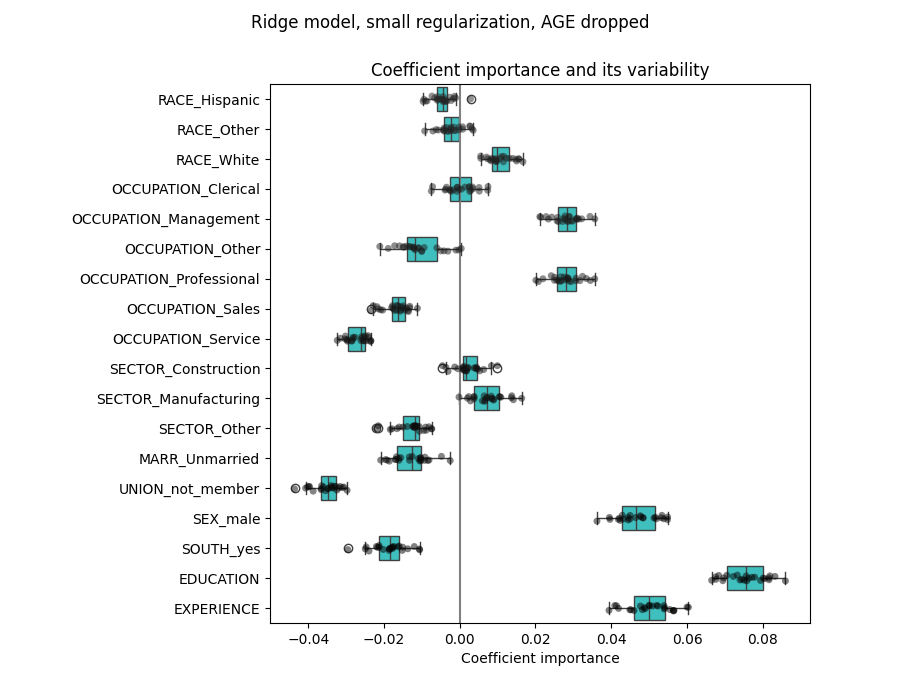
يُظهر تقدير معامل EXPERIENCE الآن تباينًا أقل بكثير. يظل EXPERIENCE مهمًا لجميع النماذج المدربة أثناء التحقق المتقاطع.
المعالجة المسبقة للمتغيرات الرقمية#
كما ذكر أعلاه (انظر "خط أنابيب التعلم الآلي")، يمكننا أيضًا اختيار قياس القيم الرقمية قبل تدريب النموذج. يمكن أن يكون هذا مفيدًا عندما نطبق قدرًا متشابهًا من التنظيم على كل منهم في ridge. تتم إعادة تعريف المعالج المسبق من أجل طرح المتوسط وقياس المتغيرات إلى تباين الوحدة.
from sklearn.preprocessing import StandardScaler
preprocessor = make_column_transformer(
(OneHotEncoder(drop="if_binary"), categorical_columns),
(StandardScaler(), numerical_columns),
)
سيبقى النموذج دون تغيير.
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
),
)
model.fit(X_train, y_train)
مرة أخرى، نتحقق من أداء النموذج المحسوب باستخدام، على سبيل المثال، متوسط الخطأ المطلق للنموذج ومعامل R التربيعي.
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
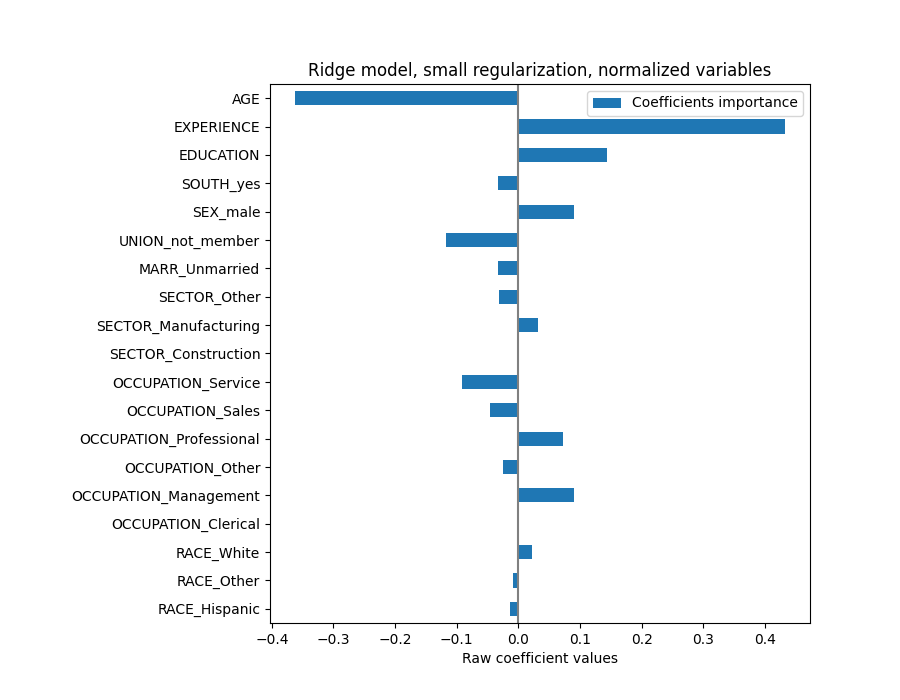
لتحليل المعامل، لا يلزم القياس هذه المرة لأنه تم إجراؤه أثناء خطوة المعالجة المسبقة.
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
نقوم الآن بفحص المعاملات عبر عدة طيات تحقق متقاطع. كما في المثال أعلاه، لا نحتاج إلى قياس المعاملات بواسطة الانحراف المعياري لقيم الميزة حيث تم بالفعل إجراء هذا القياس في خطوة المعالجة المسبقة لخط الأنابيب.
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)
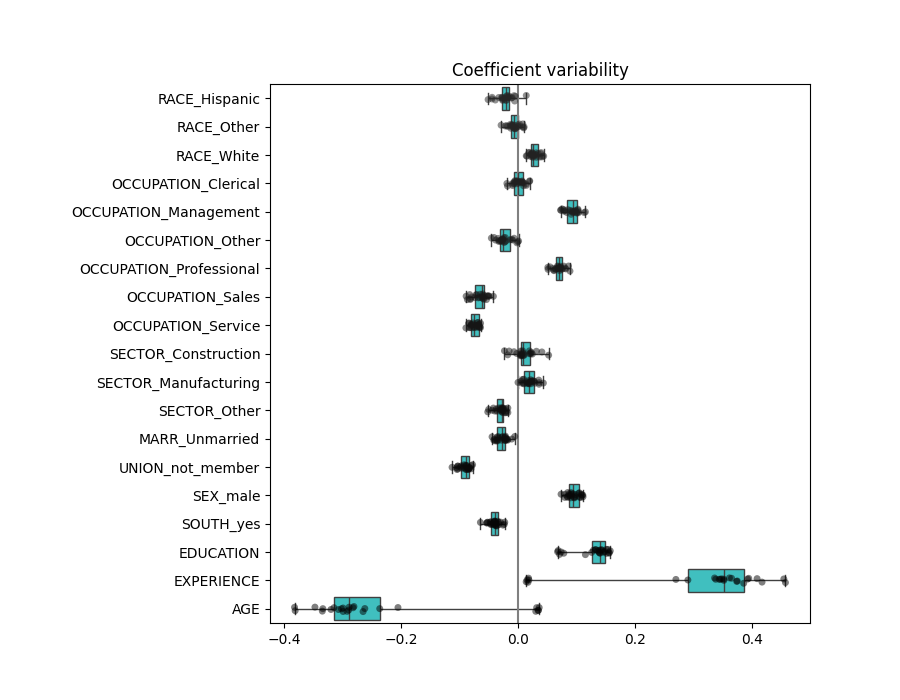
النتيجة مشابهة تمامًا للحالة غير الطبيعية.
النماذج الخطية مع التنظيم#
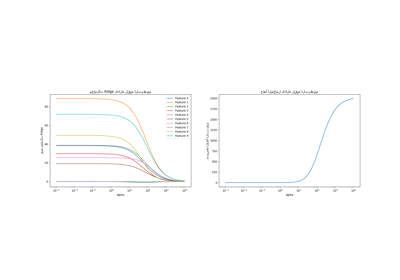
في ممارسة التعلم الآلي، غالبًا ما يُستخدم انحدار ريدج مع تنظيم غير ضئيل.
أعلاه، قمنا بتحديد هذا التنظيم إلى حد ضئيل جدًا. التنظيم
يُحسِّن حالة المشكلة ويقلل من تباين
التقديرات. RidgeCV تطبق التحقق المتقاطع
من أجل تحديد قيمة معامل التنظيم (alpha)
الأنسب للتنبؤ.
from sklearn.linear_model import RidgeCV
alphas = np.logspace(-10, 10, 21) # alpha values to be chosen from by cross-validation
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=RidgeCV(alphas=alphas),
func=np.log10,
inverse_func=sp.special.exp10,
),
)
model.fit(X_train, y_train)
أولاً نتحقق من قيمة \(\alpha\) التي تم تحديدها.
model[-1].regressor_.alpha_
np.float64(10.0)
ثم نتحقق من جودة التنبؤات.
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, optimum regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
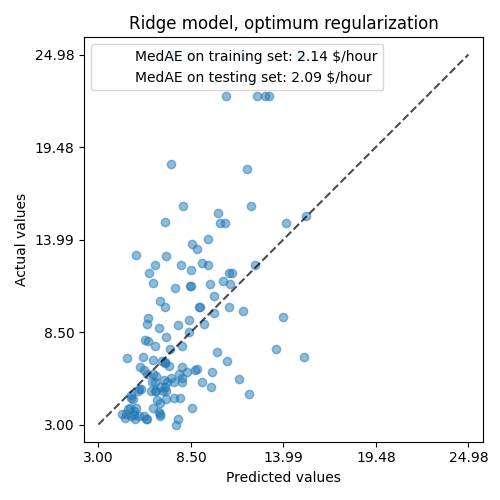
قدرة النموذج المنظم على إعادة إنتاج البيانات مشابهة لقدرة النموذج غير المنظم.
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, with regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
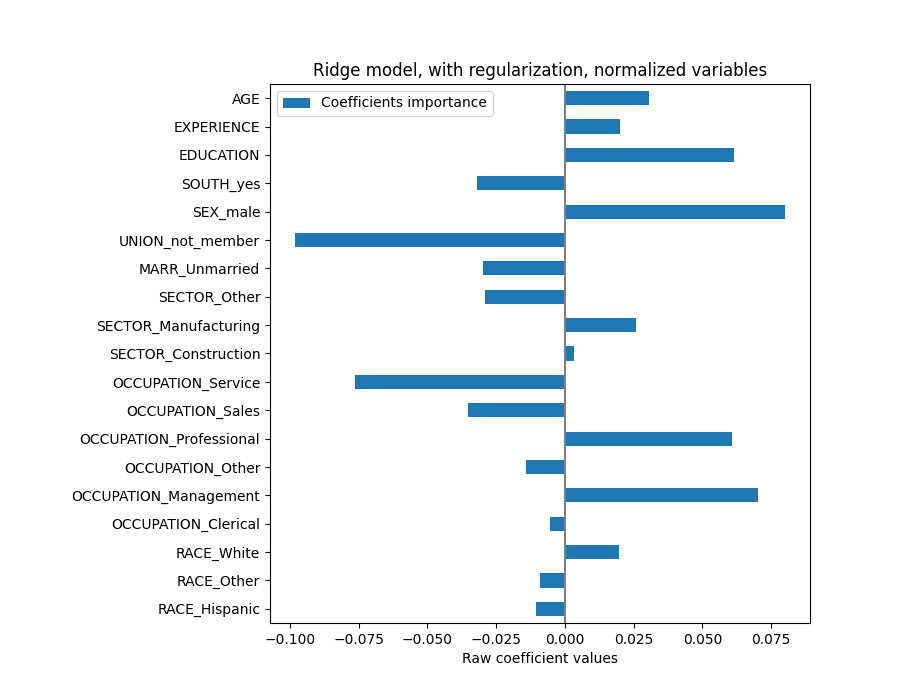
المعاملات مختلفة بشكل كبير. معاملات AGE و EXPERIENCE كلاهما موجبان لكنهما الآن لهما تأثير أقل على التنبؤ.
يقلل التنظيم من تأثير المتغيرات المترابطة على النموذج لأن الوزن مشترك بين متغيري التنبؤ، لذلك لن يكون لأي منهما أوزان قوية بمفرده.
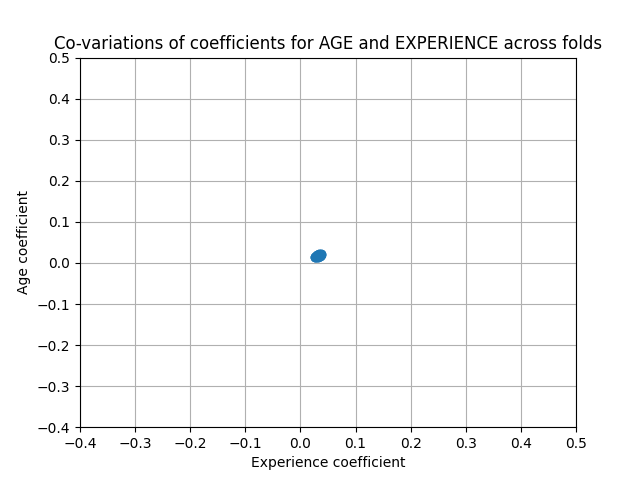
من ناحية أخرى، فإن الأوزان التي تم الحصول عليها مع التنظيم أكثر استقرارًا (انظر قسم انحدار ريدج والتصنيف في دليل المستخدم). هذا الاستقرار المتزايد واضح من الرسم التخطيطي، الذي تم الحصول عليه من اضطرابات البيانات، في تحقق متقاطع. يمكن مقارنة هذا الرسم التخطيطي بـ الرسم التخطيطي السابق.
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.ylabel("Age coefficient")
plt.xlabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")
النماذج الخطية ذات المعاملات المتفرقة#
هناك إمكانية أخرى لمراعاة المتغيرات المترابطة في مجموعة البيانات، وهي تقدير المعاملات المتفرقة. بطريقة ما فعلنا ذلك بالفعل يدويًا عندما أسقطنا عمود AGE في تقدير ريدج سابق.
تُقدِّر نماذج لاسو (انظر قسم Lasso في دليل المستخدم) المعاملات
المتفرقة. LassoCV تطبق التحقق المتقاطع
من أجل تحديد قيمة معامل التنظيم
(alpha) الأنسب لتقدير النموذج.
from sklearn.linear_model import LassoCV
alphas = np.logspace(-10, 10, 21) # alpha values to be chosen from by cross-validation
model = make_pipeline(
preprocessor,
TransformedTargetRegressor(
regressor=LassoCV(alphas=alphas, max_iter=100_000),
func=np.log10,
inverse_func=sp.special.exp10,
),
)
_ = model.fit(X_train, y_train)
أولاً، نتحقق من قيمة \(\alpha\) التي تم تحديدها.
model[-1].regressor_.alpha_
np.float64(0.001)
ثم نتحقق من جودة التنبؤات.
mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
"MedAE on training set": f"{mae_train:.2f} $/hour",
"MedAE on testing set": f"{mae_test:.2f} $/hour",
}
_, ax = plt.subplots(figsize=(6, 6))
display = PredictionErrorDisplay.from_predictions(
y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Lasso model, optimum regularization")
for name, score in scores.items():
ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()
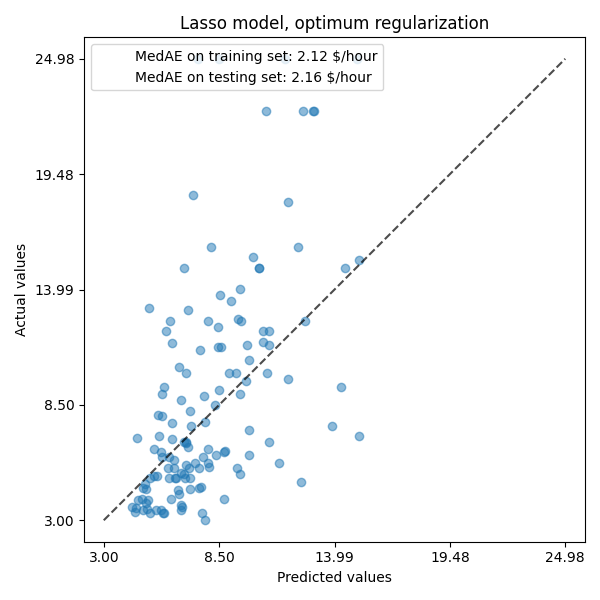
بالنسبة لمجموعة البيانات لدينا، مرة أخرى، النموذج ليس تنبئيًا للغاية.
coefs = pd.DataFrame(
model[-1].regressor_.coef_,
columns=["Coefficients importance"],
index=feature_names,
)
coefs.plot(kind="barh", figsize=(9, 7))
plt.title("Lasso model, optimum regularization, normalized variables")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)
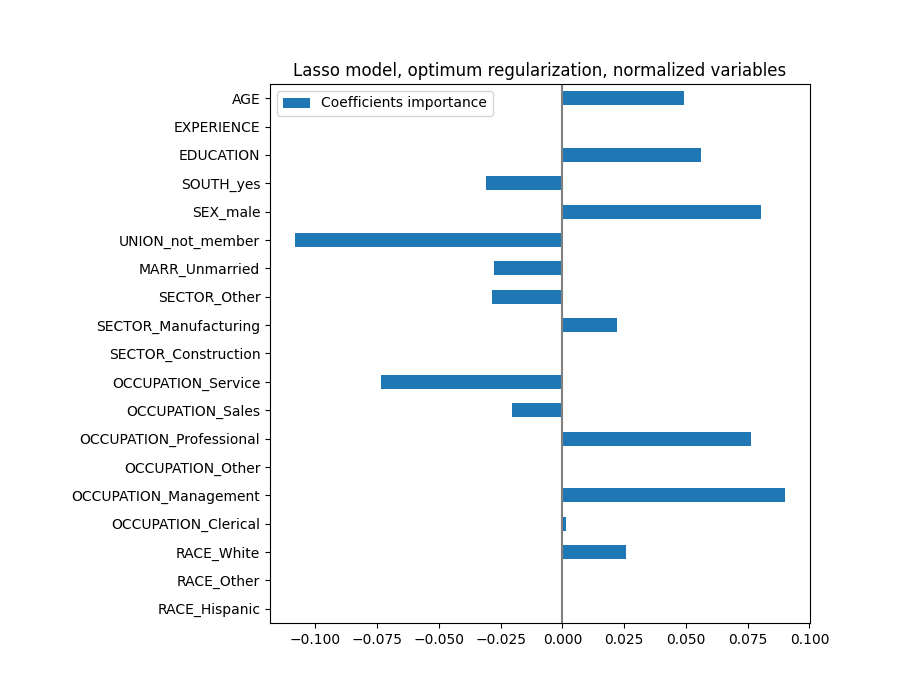
يُحدد نموذج لاسو الارتباط بين AGE و EXPERIENCE ويقمع أحدهما من أجل التنبؤ.
من المهم أن تضع في اعتبارك أن المعاملات التي تم إسقاطها قد تظل مرتبطة بالنتيجة بنفسها: اختار النموذج قمعها لأنها لا تجلب سوى القليل من المعلومات الإضافية أو لا تجلب أي معلومات إضافية على رأس الميزات الأخرى. بالإضافة إلى ذلك، يكون هذا الاختيار غير مستقر للميزات المترابطة، ويجب تفسيره بـ حذر.
في الواقع، يمكننا التحقق من تباين المعاملات عبر الطيات.
cv_model = cross_validate(
model,
X,
y,
cv=cv,
return_estimator=True,
n_jobs=2,
)
coefs = pd.DataFrame(
[est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=100)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)
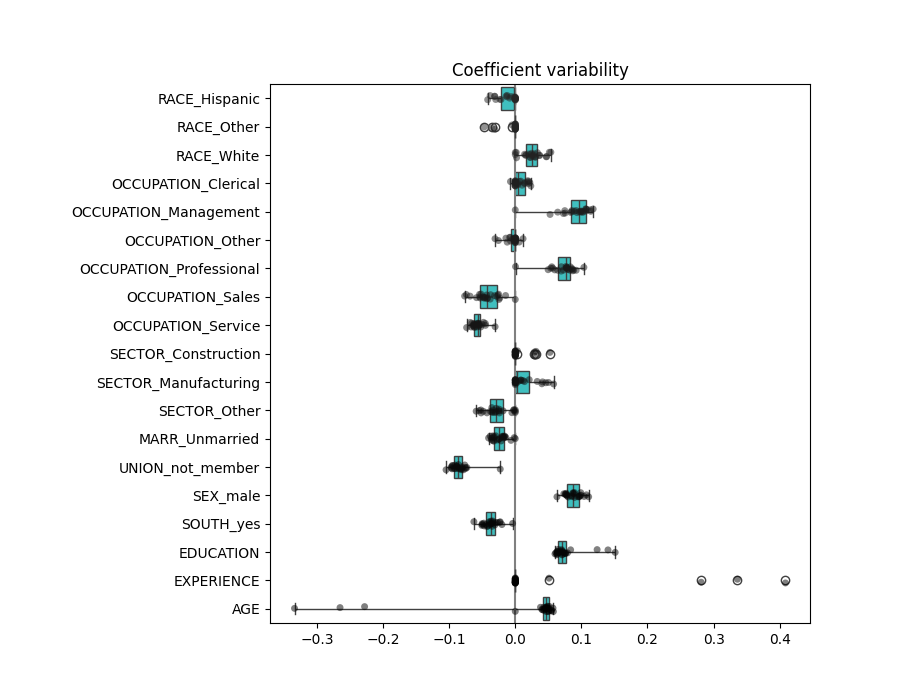
نلاحظ أن معاملات AGE و EXPERIENCE تختلف كثيرًا اعتمادًا على الطية.
التفسير السببي الخاطئ#
قد يرغب صانعو السياسات في معرفة تأثير التعليم على الأجور لتقييم ما إذا كانت سياسة معينة مصممة لجذب الناس لمتابعة المزيد من التعليم ستكون منطقية من الناحية الاقتصادية أم لا. بينما تُعد نماذج التعلم الآلي رائعة لقياس الارتباطات الإحصائية، إلا أنها غير قادرة بشكل عام على استنتاج التأثيرات السببية.
قد يكون من المغري النظر إلى معامل التعليم على الأجور من نموذجنا الأخير (أو أي نموذج في هذا الشأن) والاستنتاج بأنه يلتقط التأثير الحقيقي لتغيير في متغير التعليم المعياري على الأجور.
لسوء الحظ، من المحتمل أن تكون هناك متغيرات مرب
Total running time of the script: (0 minutes 16.063 seconds)
Related examples