ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
انحدار تويدي على مطالبات التأمين#
يوضح هذا المثال استخدام الانحدار الشعاعي، جاما وتويدي على مجموعة بيانات مطالبات المسؤولية المدنية الفرنسية لطرف ثالث، مستوحى من درس تعليمي R [1].
في هذه المجموعة من البيانات، يتوافق كل عينة مع بوليصة تأمين، أي عقد داخل شركة تأمين وفرد (حامل بوليصة التأمين). تتضمن الميزات المتاحة عمر السائق، وعمر السيارة، وقوة السيارة، وما إلى ذلك.
بعض التعريفات: المطالبة هي الطلب الذي يقدمه حامل بوليصة التأمين إلى شركة التأمين لتعويض الخسارة التي يغطيها التأمين. مبلغ المطالبة هو مبلغ المال الذي يجب على شركة التأمين دفعه. التعرض هو مدة تغطية التأمين لسياسة معينة، بالسنوات.
هنا هدفنا هو التنبؤ بالقيمة المتوقعة، أي المتوسط، لمبلغ المطالبة الإجمالي لكل وحدة تعرض، والتي يشار إليها أيضًا باسم القسط الصافي.
هناك عدة إمكانيات للقيام بذلك، اثنان منها هما:
نمذجة عدد المطالبات بتوزيع شعاعي، ومتوسط مبلغ المطالبة لكل مطالبة، المعروف أيضًا باسم الشدة، كتوزيع جاما وضرب تنبؤات كل من أجل الحصول على مبلغ المطالبة الإجمالي.
نمذجة مبلغ المطالبة الإجمالي لكل تعرض مباشرةً، عادةً بتوزيع تويدي من تويدي بقوة \(p \in (1, 2)\).
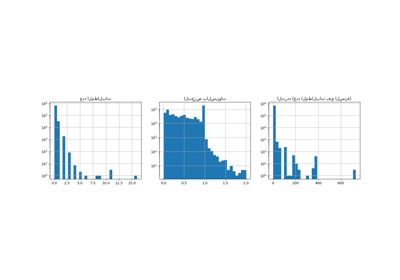
في هذا المثال، سنقوم بتوضيح كلا النهجين. نبدأ بتعريف بعض وظائف المساعدة لتحميل البيانات وتصور النتائج.
# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.metrics import (
mean_absolute_error,
mean_squared_error,
mean_tweedie_deviance,
)
def load_mtpl2(n_samples=None):
"""تحميل مجموعة بيانات مطالبات المسؤولية المدنية الفرنسية لطرف ثالث.
المعلمات
----------
n_samples: int، default=None
عدد العينات المراد تحديدها (لتشغيل وقت أسرع). تحتوي مجموعة البيانات الكاملة على
678013 عينة.
"""
# freMTPL2freq dataset from https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True).data
df_freq["IDpol"] = df_freq["IDpol"].astype(int)
df_freq.set_index("IDpol", inplace=True)
# freMTPL2sev dataset from https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True).data
# sum ClaimAmount over identical IDs
df_sev = df_sev.groupby("IDpol").sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"] = df["ClaimAmount"].fillna(0)
# unquote string fields
for column_name in df.columns[[t is object for t in df.dtypes.values]]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(
df,
feature,
weight,
observed,
predicted,
y_label=None,
title=None,
ax=None,
fill_legend=False,
):
"""رسم الملاحظ والمتوقع - مجمعة حسب مستوى الميزة.
المعلمات
----------
df : DataFrame
بيانات الإدخال
الميزة: str
اسم عمود df لميزة المراد رسمها
الوزن : str
اسم عمود df بقيم الأوزان أو التعرض
الملاحظ : str
اسم عمود df مع الهدف الملاحظ
المتوقع : DataFrame
جدول بيانات، بنفس فهرس df، مع الهدف المتوقع
fill_legend : bool، default=False
ما إذا كان سيتم عرض fill_between legend
"""
# تجميع المتغيرات الملاحظة والمتوقعة حسب مستوى الميزة
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], ["{} distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator,
X_train,
X_test,
df_train,
df_test,
target,
weights,
tweedie_powers=None,
):
"""تقييم أداة تقدير على مجموعات التدريب والاختبار بمقاييس مختلفة"""
metrics = [
("D² explained", None), # استخدم scorer الافتراضي إذا كان موجودًا
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [
(
"mean Tweedie dev p={:.4f}".format(power),
partial(mean_tweedie_deviance, power=power),
)
for power in tweedie_powers
]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# تسجيل نموذج يتكون من ناتج نموذج التردد
# والشدة.
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append({"subset": subset_label, "metric": score_label, "score": score})
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ["train", "test"]]
)
return res
تحميل مجموعات البيانات، استخراج الميزات الأساسية وتعاريف الهدف#
نحن نبني مجموعة بيانات freMTPL2 عن طريق الانضمام إلى جدول freMTPL2freq،
تحتوي على عدد المطالبات (ClaimNb)، مع جدول freMTPL2sev،
تحتوي على مبلغ المطالبة (ClaimAmount) لنفس معرفات السياسة
(IDpol).
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
FunctionTransformer,
KBinsDiscretizer,
OneHotEncoder,
StandardScaler,
)
df = load_mtpl2()
# تصحيح الملاحظات غير المعقولة (التي قد تكون خطأ في البيانات)
# وبعض مبالغ المطالبات الكبيرة بشكل استثنائي
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
# إذا كان مبلغ المطالبة 0، فلا نعتبره مطالبة. دالة الخسارة
# المستخدمة بواسطة نموذج الشدة تتطلب مبالغ مطالبات إيجابية صارمة. بهذه الطريقة
# التردد والشدة أكثر اتساقًا مع بعضهما البعض.
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log), StandardScaler()
)
column_trans = ColumnTransformer(
[
(
"binned_numeric",
KBinsDiscretizer(n_bins=10, random_state=0),
["VehAge", "DrivAge"],
),
(
"onehot_categorical",
OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"],
),
("passthrough_numeric", "passthrough", ["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer, ["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# شركات التأمين مهتمة بنمذجة القسط الصافي، أي
# مبلغ المطالبة الإجمالي المتوقع لكل وحدة من التعرض لكل حامل بوليصة في
# محفظتهم:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# يمكن تقريب هذا بشكل غير مباشر عن طريق النمذجة ذات الخطوتين: ناتج نموذج التردد
# والشدة:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
ClaimNb Exposure Area VehPower VehAge DrivAge BonusMalus VehBrand \
IDpol
139 1 0.75 F 7 1 61 50 B12
190 1 0.14 B 12 5 50 60 B12
414 1 0.14 E 4 0 36 85 B12
424 2 0.62 F 10 0 51 100 B12
463 1 0.31 A 5 0 45 50 B12
VehGas Density Region ClaimAmount PurePremium Frequency \
IDpol
139 'Regular' 27000 R11 303.00 404.000000 1.333333
190 'Diesel' 56 R25 1981.84 14156.000000 7.142857
414 'Regular' 4792 R11 1456.55 10403.928571 7.142857
424 'Regular' 27000 R11 10834.00 17474.193548 3.225806
463 'Regular' 12 R73 3986.67 12860.225806 3.225806
AvgClaimAmount
IDpol
139 303.00
190 1981.84
414 1456.55
424 5417.00
463 3986.67
نموذج التردد - التوزيع الشعاعي#
عدد المطالبات (ClaimNb) هو عدد صحيح إيجابي (0 مدرج).
وبالتالي، يمكن نمذجة هذا الهدف بتوزيع شعاعي.
يفترض بعد ذلك أن يكون عدد الأحداث المنفصلة التي تحدث بمعدل ثابت
في فترة زمنية معينة (Exposure، بوحدات السنوات).
هنا نقوم بنمذجة التردد y = ClaimNb / Exposure، والذي لا يزال
(مقياس) توزيع شعاعي، واستخدام Exposure كـ sample_weight.
from sklearn.linear_model import PoissonRegressor
from sklearn.model_selection import train_test_split
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
دعنا نضع في اعتبارنا أنه على الرغم من العدد الكبير على ما يبدو من نقاط البيانات في هذه المجموعة من البيانات، فإن عدد نقاط التقييم التي يكون فيها مبلغ المطالبة غير صفري صغير جدًا:
len(df_test)
169504
len(df_test[df_test["ClaimAmount"] > 0])
6237
ونتيجة لذلك، نتوقع تقلبًا كبيرًا في تقييمنا عند إعادة أخذ العينات العشوائية للاختبار تقسيم.
يتم تقدير معلمات النموذج عن طريق تقليل الانحراف الشعاعي
على مجموعة التدريب عبر محدد نيوتن. بعض الميزات متوازية
(على سبيل المثال لأننا لم نتخلص من أي مستوى فئوي في OneHotEncoder)،
نستخدم ضعف L2 لتجنب المشكلات العددية.
glm_freq = PoissonRegressor(alpha=1e-4, solver="newton-cholesky")
glm_freq.fit(X_train, df_train["Frequency"], sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("تقييم PoissonRegressor على الهدف Frequency")
print(scores)
تقييم PoissonRegressor على الهدف Frequency
subset train test
metric
D² explained 0.0448 0.0427
mean abs. error 0.1379 0.1378
mean squared error 0.2441 0.2246
لاحظ أن النتيجة المقاسة على مجموعة الاختبار أفضل بشكل مدهش من على مجموعة التدريب. قد يكون هذا خاصًا بهذا التقسيم العشوائي للاختبار. التدريب. يمكن للتحقق الصحيح من الصحة أن يساعدنا في تقييم تقلب العينات لهذه النتائج.
يمكننا مقارنة القيم الملاحظة والمتوقعة بصريًا، مجمعة حسب
عمر السائق (DrivAge)، عمر السيارة (VehAge) و
التأمين مكافأة/عقوبة (BonusMalus).
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True,
)
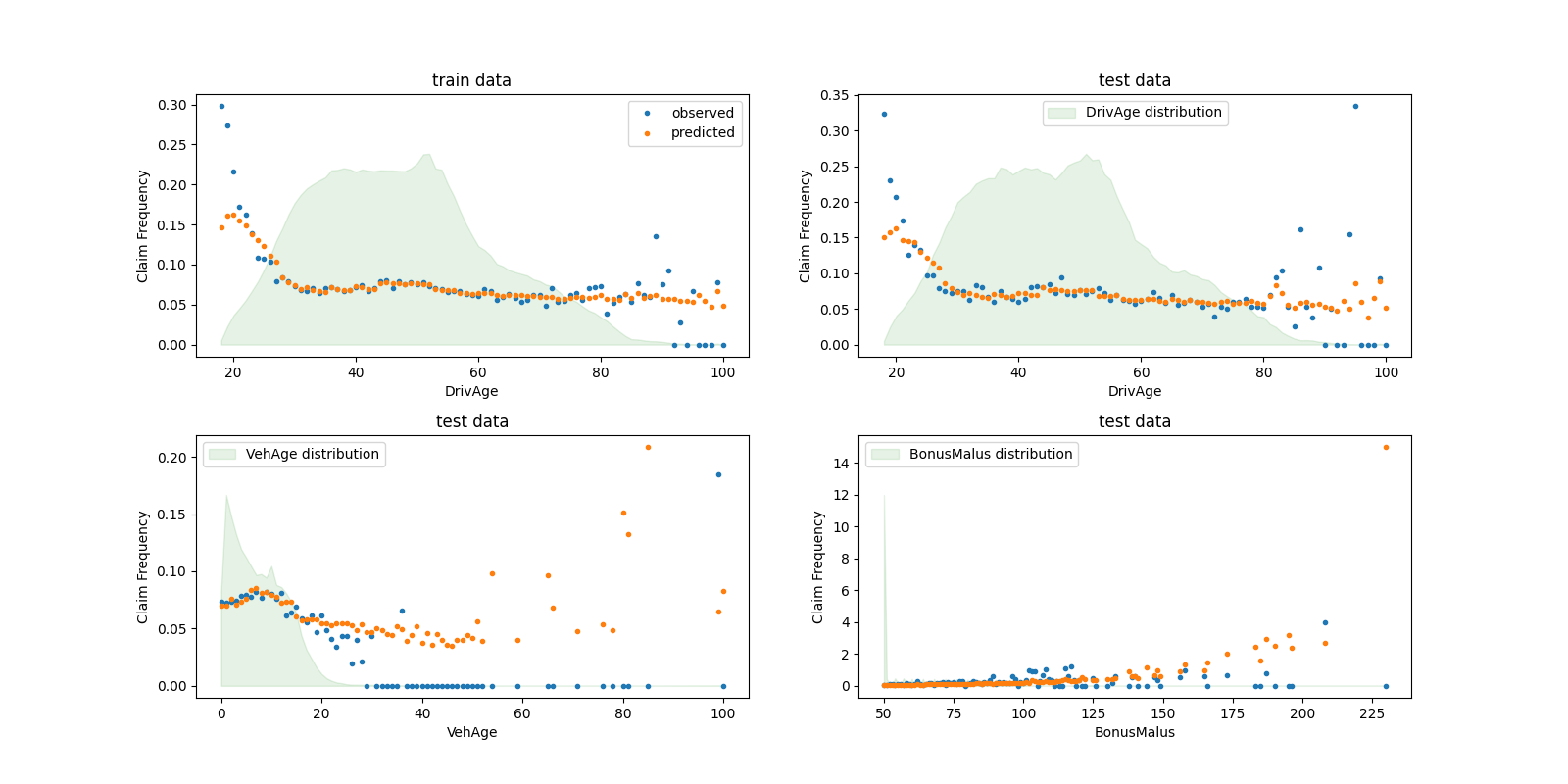
وفقًا للبيانات المرصودة، يكون معدل الحوادث أعلى بالنسبة
للسائقين الذين تقل أعمارهم عن 30 عامًا، وهو مرتبط بشكل إيجابي
بمتغير BonusMalus. نموذجنا قادر على نمذجة هذا السلوك
بشكل صحيح في الغالب.
نموذج الشدة - توزيع جاما#
يمكن إظهار أن متوسط مبلغ المطالبة أو الشدة (AvgClaimAmount)
يتبع تجريبيًا توزيع جاما تقريبًا. نقوم بملاءمة نموذج GLM
للحدة بنفس ميزات نموذج التردد.
ملاحظة:
نقوم بتصفية
ClaimAmount == 0حيث أن توزيع جاما مدعوم على \((0, \infty)\)، وليس \([0, \infty)\).نستخدم
ClaimNbكـsample_weightلحساب السياسات التي تحتوي على أكثر من مطالبة واحدة.
from sklearn.linear_model import GammaRegressor
mask_train = df_train["ClaimAmount"] > 0
mask_test = df_test["ClaimAmount"] > 0
glm_sev = GammaRegressor(alpha=10.0, solver="newton-cholesky")
glm_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
glm_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("تقييم GammaRegressor على الهدف AvgClaimAmount")
print(scores)
تقييم GammaRegressor على الهدف AvgClaimAmount
subset train test
metric
D² explained 3.900000e-03 4.400000e-03
mean abs. error 1.756746e+03 1.744042e+03
mean squared error 5.801770e+07 5.030677e+07
هذه القيم للمقاييس ليست بالضرورة سهلة التفسير. قد يكون من المفيد مقارنتها بنموذج لا يستخدم أي ميزات إدخال ويتنبأ دائمًا بقيمة ثابتة، أي متوسط مبلغ المطالبة، في نفس الإعداد:
from sklearn.dummy import DummyRegressor
dummy_sev = DummyRegressor(strategy="mean")
dummy_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
dummy_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("تقييم متنبئ متوسط على الهدف AvgClaimAmount")
print(scores)
تقييم متنبئ متوسط على الهدف AvgClaimAmount
subset train test
metric
D² explained 0.000000e+00 -0.000000e+00
mean abs. error 1.756687e+03 1.744497e+03
mean squared error 5.803882e+07 5.033764e+07
نستنتج أن مبلغ المطالبة من الصعب جدًا التنبؤ به. ومع ذلك، فإن
GammaRegressor قادر على الاستفادة من بعض
المعلومات من ميزات الإدخال لتحسين خط الأساس المتوسط
قليلاً من حيث D².
لاحظ أن النموذج الناتج هو متوسط مبلغ المطالبة لكل مطالبة. على هذا النحو، فهو مشروط بوجود مطالبة واحدة على الأقل، ولا يمكن استخدامه للتنبؤ بمتوسط مبلغ المطالبة لكل سياسة. لهذا، يجب دمجه مع نموذج لتكرار المطالبات.
print(
"متوسط مبلغ AvgClaim لكل سياسة: %.2f "
% df_train["AvgClaimAmount"].mean()
)
print(
"متوسط مبلغ AvgClaim | NbClaim > 0: %.2f"
% df_train["AvgClaimAmount"][df_train["AvgClaimAmount"] > 0].mean()
)
print(
"متوسط مبلغ AvgClaim المتوقع | NbClaim > 0: %.2f"
% glm_sev.predict(X_train).mean()
)
print(
"متوسط مبلغ AvgClaim المتوقع (وهمي) | NbClaim > 0: %.2f"
% dummy_sev.predict(X_train).mean()
)
متوسط مبلغ AvgClaim لكل سياسة: 71.78
متوسط مبلغ AvgClaim | NbClaim > 0: 1951.21
متوسط مبلغ AvgClaim المتوقع | NbClaim > 0: 1940.95
متوسط مبلغ AvgClaim المتوقع (وهمي) | NbClaim > 0: 1978.59
يمكننا مقارنة القيم المرصودة والمتوقعة بصريًا، مجمعة
لعمر السائقين (DrivAge).
fig, ax = plt.subplots(ncols=1, nrows=2, figsize=(16, 6))
plot_obs_pred(
df=df_train.loc[mask_train],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_train[mask_train.values]),
y_label="متوسط حدة المطالبة",
title="بيانات التدريب",
ax=ax[0],
)
plot_obs_pred(
df=df_test.loc[mask_test],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_test[mask_test.values]),
y_label="متوسط حدة المطالبة",
title="بيانات الاختبار",
ax=ax[1],
fill_legend=True,
)
plt.tight_layout()
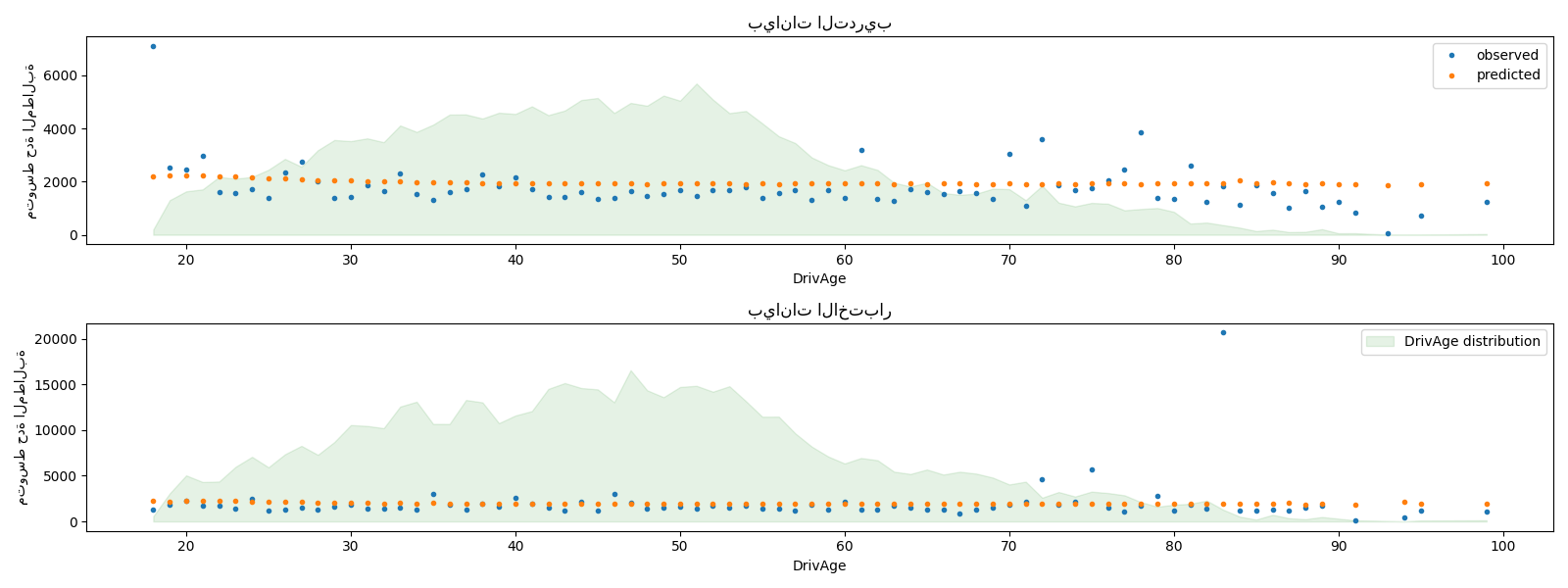
بشكل عام، يكون لعمر السائقين (DrivAge) تأثير ضعيف على حدة
المطالبة، سواء في البيانات المرصودة أو المتوقعة.
نمذجة القسط الخالص عبر نموذج المنتج مقابل TweedieRegressor واحد#
كما هو مذكور في المقدمة، يمكن نمذجة إجمالي مبلغ المطالبة لكل وحدة تعرض على أنه حاصل ضرب تنبؤ نموذج التردد في تنبؤ نموذج الشدة.
بدلاً من ذلك، يمكن للمرء نمذجة الخسارة الإجمالية مباشرة باستخدام نموذج خطي
معمم مركب Poisson Gamma فريد (مع دالة ربط لوغاريتمي).
هذا النموذج هو حالة خاصة من Tweedie GLM مع معلمة "قوة"
\(p \in (1, 2)\). هنا، نقوم بتثبيت معلمة power لنموذج
Tweedie مسبقًا على قيمة عشوائية (1.9) في النطاق الصحيح. من الناحية المثالية،
سيختار المرء هذه القيمة عبر البحث الشبكي عن طريق تقليل
احتمالية السجل السالب لنموذج Tweedie، لكن لسوء الحظ، لا يسمح
التطبيق الحالي بذلك (حتى الآن).
سنقارن أداء كلا النهجين.
لتحديد أداء كلا النموذجين كميًا، يمكن للمرء حساب
متوسط انحراف بيانات التدريب والاختبار بافتراض توزيع
مركب Poisson-Gamma لإجمالي مبلغ المطالبة. هذا يعادل
توزيع Tweedie مع معلمة power بين 1 و 2.
تعتمد sklearn.metrics.mean_tweedie_deviance على معلمة power.
نظرًا لأننا لا نعرف القيمة الحقيقية لمعلمة power، فإننا هنا نحسب
متوسط الانحرافات لشبكة من القيم الممكنة، ونقارن النماذج جنبًا إلى جنب،
أي أننا نقارنها بقيم متطابقة لـ power. من الناحية المثالية، نأمل أن يكون أحد
النماذج أفضل باستمرار من الآخر، بغض النظر عن power.
from sklearn.linear_model import TweedieRegressor
glm_pure_premium = TweedieRegressor(power=1.9, alpha=0.1, solver="newton-cholesky")
glm_pure_premium.fit(
X_train, df_train["PurePremium"], sample_weight=df_train["Exposure"]
)
tweedie_powers = [1.5, 1.7, 1.8, 1.9, 1.99, 1.999, 1.9999]
scores_product_model = score_estimator(
(glm_freq, glm_sev),
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores_glm_pure_premium = score_estimator(
glm_pure_premium,
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores = pd.concat(
[scores_product_model, scores_glm_pure_premium],
axis=1,
sort=True,
keys=("نموذج المنتج", "TweedieRegressor"),
)
print(
"تقييم نموذج المنتج و Tweedie Regressor على الهدف PurePremium"
)
with pd.option_context("display.expand_frame_repr", False):
print(scores)
تقييم نموذج المنتج و Tweedie Regressor على الهدف PurePremium
نموذج المنتج TweedieRegressor
subset train test train test
metric
D² explained NaN NaN 1.640000e-02 1.370000e-02
mean Tweedie dev p=1.5000 7.669930e+01 7.617050e+01 7.640770e+01 7.640880e+01
mean Tweedie dev p=1.7000 3.695740e+01 3.683980e+01 3.682880e+01 3.692270e+01
mean Tweedie dev p=1.8000 3.046010e+01 3.040530e+01 3.037600e+01 3.045390e+01
mean Tweedie dev p=1.9000 3.387580e+01 3.385000e+01 3.382120e+01 3.387830e+01
mean Tweedie dev p=1.9900 2.015716e+02 2.015414e+02 2.015347e+02 2.015587e+02
mean Tweedie dev p=1.9990 1.914573e+03 1.914370e+03 1.914538e+03 1.914387e+03
mean Tweedie dev p=1.9999 1.904751e+04 1.904556e+04 1.904747e+04 1.904558e+04
mean abs. error 2.730119e+02 2.722128e+02 2.739865e+02 2.731249e+02
mean squared error 3.295040e+07 3.212197e+07 3.295505e+07 3.213056e+07
في هذا المثال، ينتج عن كلا النهجين للنمذجة مقاييس أداء قابلة للمقارنة. لأسباب تتعلق بالتنفيذ، فإن نسبة التباين الموضحة \(D^2\) غير متاحة لنموذج المنتج.
يمكننا بالإضافة إلى ذلك التحقق من صحة هذه النماذج من خلال مقارنة إجمالي مبلغ المطالبة المرصود والمتوقع على مجموعات بيانات الاختبار والتدريب الفرعية. نرى أنه في المتوسط، يميل كلا النموذجين إلى التقليل من شأن إجمالي المطالبة (لكن هذا السلوك يعتمد على مقدار التنظيم).
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
exposure = df["Exposure"].values
res.append(
{
"subset": subset_label,
"observed": df["ClaimAmount"].values.sum(),
"predicted, frequency*severity model": np.sum(
exposure * glm_freq.predict(X) * glm_sev.predict(X)
),
"predicted, tweedie, power=%.2f"
% glm_pure_premium.power: np.sum(exposure * glm_pure_premium.predict(X)),
}
)
print(pd.DataFrame(res).set_index("subset").T)
subset train test
observed 3.917618e+07 1.299546e+07
predicted, frequency*severity model 3.916555e+07 1.313276e+07
predicted, tweedie, power=1.90 3.951751e+07 1.325198e+07
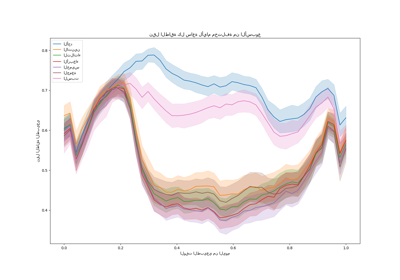
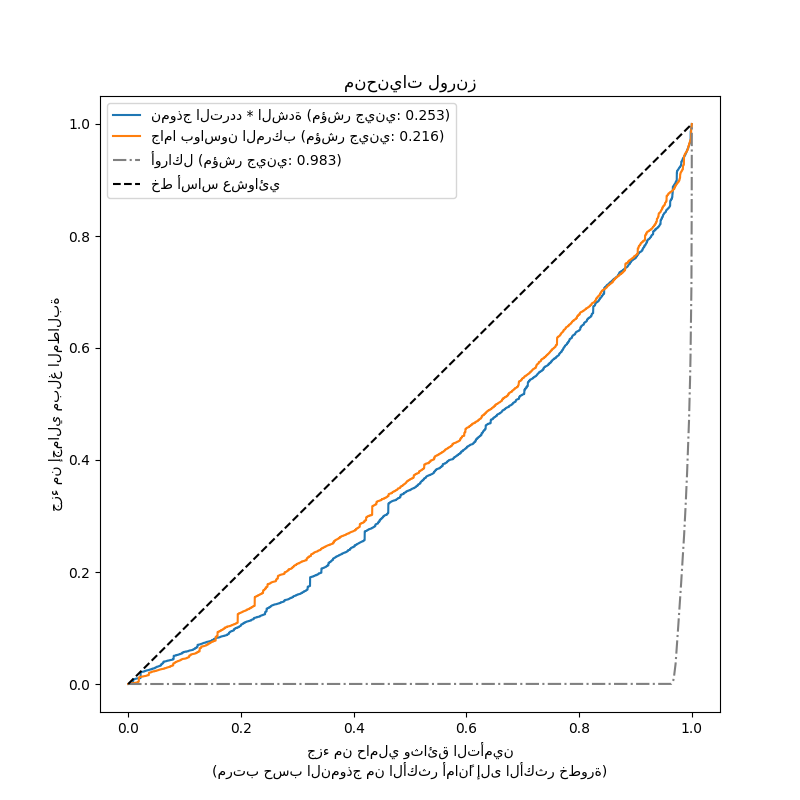
أخيرًا، يمكننا مقارنة النموذجين باستخدام مخطط المطالبات التراكمية: لكل نموذج، يتم تصنيف حاملي وثائق التأمين من الأكثر أمانًا إلى الأكثر خطورة بناءً على تنبؤات النموذج ويتم رسم جزء من إجمالي المطالبات التراكمية المرصودة على المحور ص. غالبًا ما يُطلق على هذا الرسم البياني منحنى لورنز المرتب للنموذج.
يمكن استخدام معامل جيني (بناءً على المساحة بين المنحنى والقطر) كمقياس لاختيار النموذج لتحديد قدرة النموذج على تصنيف حاملي وثائق التأمين. لاحظ أن هذا المقياس لا يعكس قدرة النماذج على إجراء تنبؤات دقيقة من حيث القيمة المطلقة لإجمالي مبالغ المطالبات ولكن فقط من حيث الكميات النسبية كمقياس تصنيف. يكون معامل جيني محددًا بحد أقصى قدره 1.0 ولكن حتى نموذج أوراكل يصنف حاملي وثائق التأمين حسب مبالغ المطالبات المرصودة لا يمكنه الوصول إلى درجة 1.0.
نلاحظ أن كلا النموذجين قادران على تصنيف حاملي وثائق التأمين حسب الخطورة بشكل أفضل بكثير من الصدفة على الرغم من أنهما بعيدان أيضًا عن نموذج أوراكل نظرًا لصعوبة مشكلة التنبؤ الطبيعية من عدد قليل من الميزات: معظم الحوادث لا يمكن التنبؤ بها ويمكن أن تكون ناجمة عن ظروف بيئية غير موصوفة على الإطلاق بواسطة ميزات الإدخال للنماذج.
لاحظ أن مؤشر جيني يميز فقط أداء تصنيف النموذج ولكن ليس معايرته: أي تحويل رتيب للتنبؤات يترك مؤشر جيني للنموذج دون تغيير.
أخيرًا، ينبغي للمرء أن يؤكد أن نموذج جاما Poisson المركب الذي يتم ملاءمته مباشرة على القسط الخالص هو أبسط من الناحية التشغيلية للتطوير والصيانة لأنه يتكون من مقدر scikit-learn واحد بدلاً من زوج من النماذج، لكل منها مجموعته الخاصة من المعلمات الفائقة.
from sklearn.metrics import auc
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# ترتيب العينات عن طريق زيادة المخاطر المتوقعة:
ranking = np.argsort(y_pred)
ranked_exposure = exposure[ranking]
ranked_pure_premium = y_true[ranking]
cumulated_claim_amount = np.cumsum(ranked_pure_premium * ranked_exposure)
cumulated_claim_amount /= cumulated_claim_amount[-1]
cumulated_samples = np.linspace(0, 1, len(cumulated_claim_amount))
return cumulated_samples, cumulated_claim_amount
fig, ax = plt.subplots(figsize=(8, 8))
y_pred_product = glm_freq.predict(X_test) * glm_sev.predict(X_test)
y_pred_total = glm_pure_premium.predict(X_test)
for label, y_pred in [
("نموذج التردد * الشدة", y_pred_product),
("جاما بواسون المركب", y_pred_total),
]:
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], y_pred, df_test["Exposure"]
)
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label += " (مؤشر جيني: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-", label=label)
# نموذج أوراكل: y_pred == y_test
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], df_test["PurePremium"], df_test["Exposure"]
)
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label = "أوراكل (مؤشر جيني: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-.", color="gray", label=label)
# خط أساس عشوائي
ax.plot([0, 1], [0, 1], linestyle="--", color="black", label="خط أساس عشوائي")
ax.set(
title="منحنيات لورنز",
xlabel="جزء من حاملي وثائق التأمين\n(مرتب حسب النموذج من الأكثر أمانًا إلى الأكثر خطورة)",
ylabel="جزء من إجمالي مبلغ المطالبة",
)
ax.legend(loc="upper left")
plt.plot()
[]
Total running time of the script: (0 minutes 9.881 seconds)
Related examples