ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
اختيار نموذج لاصو عبر معايير المعلومات#
هذا المثال يعيد إنتاج مثال الشكل 2 من [ZHT2007]. يقوم مقدر LassoLarsIC بالتناسب مع مجموعة بيانات مرض السكري ويتم استخدام معياري معلومات أكايكي (AIC) ومعلومات بايز (BIC) لاختيار أفضل نموذج.
ملاحظة
من المهم ملاحظة أن التحسين للعثور على alpha مع
LassoLarsIC يعتمد على معياري AIC أو BIC
اللذين يتم حسابهما داخل العينة، وبالتالي على مجموعة التدريب مباشرة.
يختلف هذا النهج عن إجراء التحقق من الصحة المتقاطع. لمقارنة النهجين، يمكنك الرجوع إلى المثال التالي:
نموذج لاصو: اختيار النموذج باستخدام معايير AIC-BIC والتحقق المتقاطع.
المراجع
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
سنستخدم مجموعة بيانات مرض السكري.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
n_samples = X.shape[0]
X.head()
يوفر سكايلرن مقدرًا يسمى
LassoLarsIC الذي يستخدم إما معيار معلومات أكايكي (AIC) أو معيار معلومات بايز (BIC) ل
اختيار أفضل نموذج. قبل تناسب
هذا النموذج، سنقوم بتصغير مجموعة البيانات.
في ما يلي، سنقوم بتناسب نموذجين لمقارنة القيم المبلغ عنها من قبل AIC و BIC.
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
لكي نكون على نفس الخط مع التعريف في [ZHT2007]، نحتاج إلى إعادة تصغير AIC و BIC. في الواقع، يتجاهل Zou et al. بعض المصطلحات الثابتة مقارنة بالتعريف الأصلي لـ AIC المشتق من اللوغاريتم الأقصى لنموذج خطي. يمكنك الرجوع إلى قسم التفاصيل الرياضية لدليل المستخدم.
import numpy as np
aic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_aic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
bic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_bic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
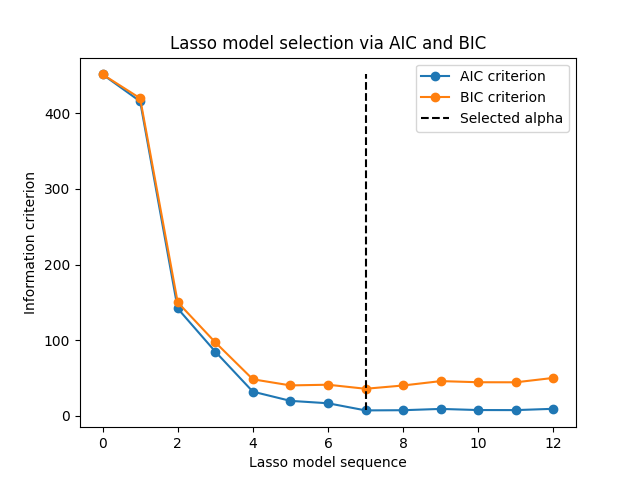
الآن بعد أن جمعنا AIC و BIC، يمكننا أيضًا التحقق من أن الحد الأدنى لكل من المعايير يحدث عند نفس alpha. بعد ذلك، يمكننا تبسيط الرسم البياني التالي.
index_alpha_path_aic == index_alpha_path_bic
np.True_
أخيرًا، يمكننا رسم معيار AIC و BIC والمعلمة المنتظمة اللاحقة.
import matplotlib.pyplot as plt
plt.plot(aic_criterion, color="tab:blue", marker="o", label="AIC criterion")
plt.plot(bic_criterion, color="tab:orange", marker="o", label="BIC criterion")
plt.vlines(
index_alpha_path_bic,
aic_criterion.min(),
aic_criterion.max(),
color="black",
linestyle="--",
label="Selected alpha",
)
plt.legend()
plt.ylabel("Information criterion")
plt.xlabel("Lasso model sequence")
_ = plt.title("Lasso model selection via AIC and BIC")
Total running time of the script: (0 minutes 0.337 seconds)
Related examples
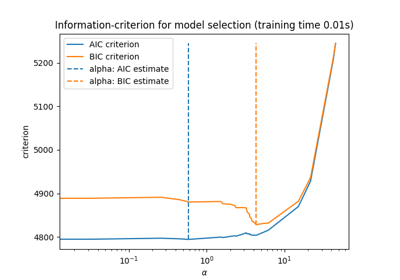
نموذج لاصو: اختيار النموذج باستخدام معايير AIC-BIC والتحقق المتقاطع