ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

نماذج L1 للاشارات المتناثرة#

يقارن المثال الحالي ثلاثة نماذج ارتجاع L1 على إشارة اصطناعية تم الحصول عليها من ميزات متناثرة ومتناسقة يتم إفسادها مع ضوضاء غاوسية إضافية:

من المعروف أن تقديرات Lasso تقترب من تقديرات اختيار النموذج عندما تنمو أبعاد البيانات، بشرط ألا تكون المتغيرات غير ذات صلة غير مرتبطة بالمتغيرات ذات الصلة. في وجود ميزات مترابطة لا يمكن للاسو نفسه اختيار نمط التبعثر [1].

نقارن هنا أداء النماذج الثلاثة من حيث درجة $R^2$ النتيجة، وقت التجهيز وتباعد المعاملات المقدرة عند مقارنة مع الحقيقة.

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

توليد مجموعة بيانات اصطناعية#

نولد مجموعة بيانات حيث يكون عدد العينات أقل من العدد الإجمالي عدد الميزات. يؤدي هذا إلى نظام غير محدد، أي أن الحل غير فريد، وبالتالي لا يمكننا تطبيق المربعات الصغرى العادية بنفسه. يقدم الانتظام مصطلح عقوبة لدالة الهدف، الذي يعدل مشكلة التحسين ويمكن أن يساعد في تخفيف الطبيعة غير المحددة للنظام.

الهدف y هو تركيبة ذات علامات متناوبة للإشارات الجيبية. تستخدم فقط 10 أدنى من 100 تردد في X لتوليد y، في حين أن بقية الميزات غير مفيدة. يؤدي هذا إلى مساحة ميزة متناثرة عالية الأبعاد، حيث تكون بعض درجات العقوبة L1 ضرورية.

import numpy as np

rng = np.random.RandomState(0)
n_samples, n_features, n_informative = 50, 100, 10
time_step = np.linspace(-2, 2, n_samples)
freqs = 2 * np.pi * np.sort(rng.rand(n_features)) / 0.01
X = np.zeros((n_samples, n_features))

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step)

idx = np.arange(n_features)
true_coef = (-1) ** idx * np.exp(-idx / 10)
true_coef[n_informative:] = 0  # sparsify coef
y = np.dot(X, true_coef)

بعض الميزات المعلوماتية لها ترددات قريبة لإدخال (مضاد) الارتباطات.

freqs[:n_informative]

array([ 2.9502547 , 11.8059798 , 12.63394388, 12.70359377, 24.62241605,
       37.84077985, 40.30506066, 44.63327171, 54.74495357, 59.02456369])

يتم إدخال مرحلة عشوائية باستخدام numpy.random.random_sample ويتم إضافة بعض الضوضاء الغاوسية (المنفذة بواسطة numpy.random.normal) إلى كل من الميزات والهدف.

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step + 2 * (rng.random_sample() - 0.5))
    X[:, i] += 0.2 * rng.normal(0, 1, n_samples)

y += 0.2 * rng.normal(0, 1, n_samples)

يمكن الحصول على مثل هذه الميزات المتناثرة والضوضاء والمرتبطة، على سبيل المثال، من عقد المستشعرات التي تراقب بعض المتغيرات البيئية، حيث أنها تسجل عادة قيم مماثلة اعتمادا على مواقفها (الارتباطات المكانية). يمكننا تصور الهدف.

import matplotlib.pyplot as plt

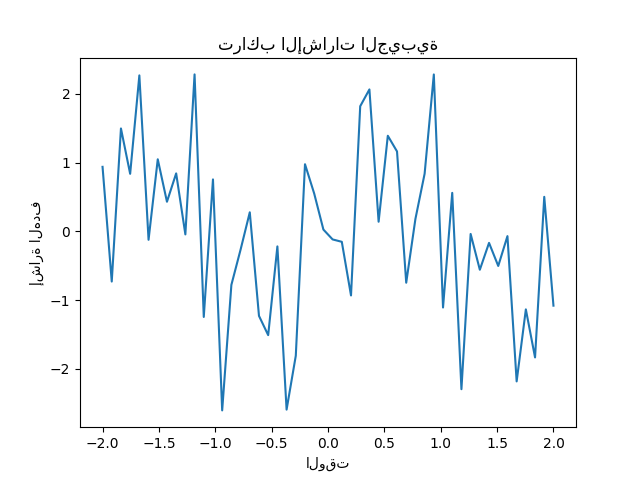
plt.plot(time_step, y)
plt.ylabel("إشارة الهدف")
plt.xlabel("الوقت")
_ = plt.title("تراكب الإشارات الجيبية")

نقسم البيانات إلى مجموعات تدريب واختبار للبساطة. في الممارسة العملية يجب استخدام TimeSeriesSplit التحقق من صحة التقاطع لتقدير تباين نتيجة الاختبار. هنا نحدد shuffle="False" حيث يجب ألا نستخدم بيانات تدريب تنجح في اختبار البيانات عند التعامل مع البيانات التي لها علاقة زمنية.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=False)

في ما يلي، نحسب أداء ثلاثة نماذج L1 من حيث جودة الملاءمة $R^2$ النتيجة ووقت التجهيز. ثم نقوم برسم تخطيطي لمقارنة تبعثر المعاملات المقدرة فيما يتعلق المعاملات الحقيقية وأخيرا نقوم بتحليل النتائج السابقة.

Lasso#

في هذا المثال، نقوم بتجربة Lasso بقيمة ثابتة قيمة معلمة الانتظام alpha. في الممارسة العملية، يجب اختيار المعلمة المثلى alpha عن طريق تمرير TimeSeriesSplit استراتيجية التحقق من الصحة المتقاطعة إلى LassoCV. للحفاظ على المثال بسيط وسريع للتنفيذ، نقوم بتعيين القيمة المثلى لـ alpha هنا مباشرة.

from time import time
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score

t0 = time()
lasso = Lasso(alpha=0.14).fit(X_train, y_train)
print(f"Lasso fit done in {(time() - t0):.3f}s")

y_pred_lasso = lasso.predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(f"Lasso r^2 on test data : {r2_score_lasso:.3f}")

Lasso fit done in 0.001s
Lasso r^2 on test data : 0.480

تحديد الأهمية التلقائي (ARD)#

إن تحديد الأهمية التلقائي هو النسخة البايزية من Lasso. يمكن أن ينتج تقديرات الفاصل الزمني لجميع المعلمات، بما في ذلك تباين الخطأ، إذا المطلوبة. إنه خيار مناسب عندما تحتوي الإشارات على ضوضاء غاوسية. انظر المثال # مقارنة المنحنيات الخطية للانحدار البايزي لمقارنة ARDRegression و BayesianRidge المنحنيات.

from sklearn.linear_model import ARDRegression

t0 = time()
ard = ARDRegression().fit(X_train, y_train)
print(f"ARD fit done in {(time() - t0):.3f}s")

y_pred_ard = ard.predict(X_test)
r2_score_ard = r2_score(y_test, y_pred_ard)
print(f"ARD r^2 on test data : {r2_score_ard:.3f}")

ARD fit done in 0.012s
ARD r^2 on test data : 0.543

ElasticNet#

ElasticNet هو أرضية وسط بين Lasso و Ridge، حيث يجمع بين عقوبة L1 و L2. يتم التحكم في كمية الانتظام يتم التحكم في المعاملين l1_ratio و alpha. لـ l1_ratio = 0 العقوبة هي L2 نقية والنموذج مكافئ Ridge. وبالمثل، l1_ratio = 1 هو عقوبة L1 نقية والنموذج مكافئ لـ Lasso. لـ 0 < l1_ratio < 1، العقوبة هي مزيج من L1 و L2.

كما فعلنا من قبل، نقوم بتدريب النموذج مع قيم ثابتة لـ alpha و l1_ratio. لاختيار قيمتهم المثلى، استخدمنا ElasticNetCV، غير معروض هنا للحفاظ على المثال بسيط.

from sklearn.linear_model import ElasticNet

t0 = time()
enet = ElasticNet(alpha=0.08, l1_ratio=0.5).fit(X_train, y_train)
print(f"ElasticNet fit done in {(time() - t0):.3f}s")

y_pred_enet = enet.predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(f"ElasticNet r^2 on test data : {r2_score_enet:.3f}")

ElasticNet fit done in 0.001s
ElasticNet r^2 on test data : 0.636

رسم وتحليل النتائج#

في هذا القسم، نستخدم خريطة حرارية لتصور تبعثر المعاملات الحقيقية والمعاملات المقدرة للنماذج الخطية المقابلة.

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.colors import SymLogNorm

df = pd.DataFrame(
    {
        "True coefficients": true_coef,
        "Lasso": lasso.coef_,
        "ARDRegression": ard.coef_,
        "ElasticNet": enet.coef_,
    }
)

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-1, vmax=1),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("النموذج الخطي")
plt.xlabel("المعاملات")
plt.title(
    f"Models' coefficients\nLasso $R^2$: {r2_score_lasso:.3f}, "
    f"ARD $R^2$: {r2_score_ard:.3f}, "
    f"ElasticNet $R^2$: {r2_score_enet:.3f}"
)
plt.tight_layout()

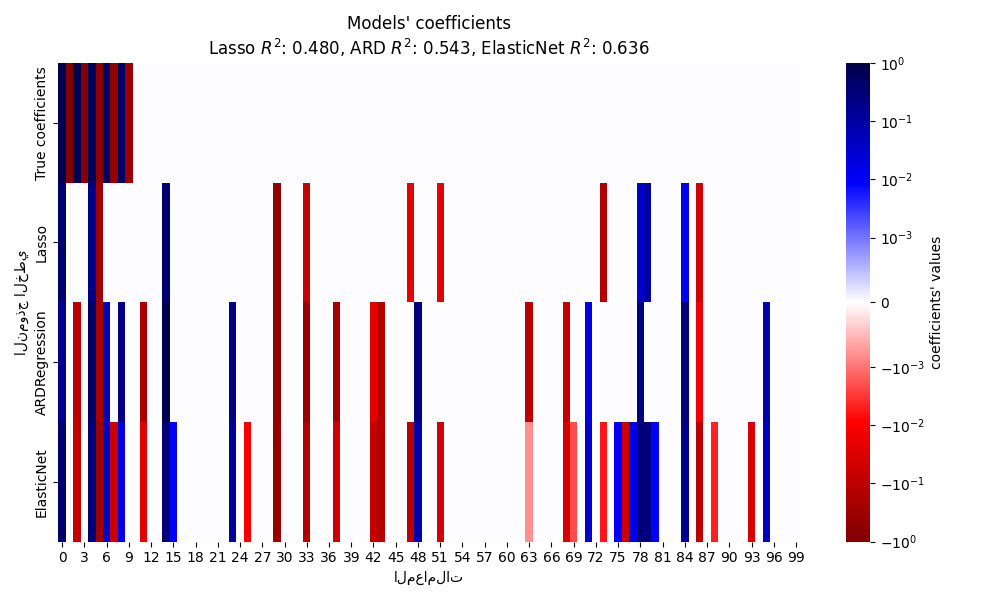
Models' coefficients Lasso $R^2$: 0.480, ARD $R^2$: 0.543, ElasticNet $R^2$: 0.636

في المثال الحالي ElasticNet يعطي أفضل نتيجة ويستخلص معظم الميزات التنبؤية، ولكنه يفشل في العثور على جميع المكونات الحقيقية. لاحظ أن كلا من ElasticNet و ARDRegression ينتج عنه نموذج أقل تبعثرا من Lasso.

الاستنتاجات#

Lasso معروف باستعادة البيانات المتناثرة بشكل فعال ولكنه لا يؤدي أداء جيدا مع الميزات المترابطة بشدة. في الواقع، إذا ساهمت العديد من الميزات المترابطة في الهدف، Lasso سينتهي الأمر باختيار واحد منها. في حالة الميزات المتناثرة ولكن غير المترابطة، سيكون نموذج Lasso أكثر ملاءمة.

ElasticNet يقدم بعض التبعثر على المعاملات ويقلل قيمها إلى الصفر. وبالتالي، في وجود الميزات المترابطة التي تساهم في الهدف، لا يزال النموذج قادرا على تقليل أوزانها دون تعيينها بالضبط إلى الصفر. يؤدي هذا إلى نموذج أقل تبعثرا من Lasso نقي وقد يلتقط الميزات غير التنبؤية كذلك.

ARDRegression أفضل في التعامل مع الضوضاء الغاوسية، ولكنه لا يزال غير قادر على التعامل مع الميزات المترابطة ويتطلب قدرا أكبر من الوقت بسبب ملاءمة السابقة.

المراجع#

Total running time of the script: (0 minutes 0.566 seconds)

Related examples

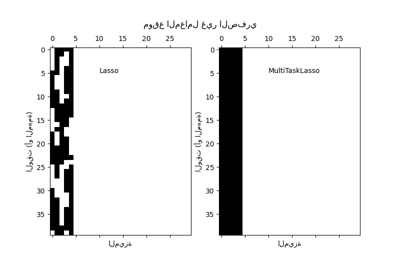
Lasso على البيانات الكثيفة والمتفرقة

الاختيار المشترك للميزات باستخدام Lasso متعدد المهام

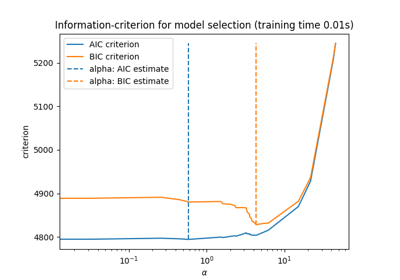
تأثير تنظيم النموذج على خطأ التدريب والاختبار

نموذج لاصو: اختيار النموذج باستخدام معايير AIC-BIC والتحقق المتقاطع

Gallery generated by Sphinx-Gallery