ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
انحدار بواسون والخسارة غير الطبيعية#
يوضح هذا المثال استخدام الانحدار اللوغاريتمي الخطي بواسون على مجموعة بيانات مطالبات المسؤولية الطرفية الثالثة للسيارات الفرنسية من [1] ويقارنها بنموذج خطي يتم تركيبه باستخدام خطأ المربعات الأقل المعتاد ونموذج GBRT غير خطي يتم تركيبه باستخدام خسارة بواسون (ورابط تسجيل الدخول).
بعض التعريفات:
السياسة هي عقد بين شركة تأمين وفرد: **حامل الوثيقة، أي سائق السيارة في هذه الحالة.
المطالبة هي الطلب الذي يقدمه حامل الوثيقة إلى شركة التأمين لتعويضه عن خسارة مغطاة بالتأمين.
التعرض هو مدة تغطية التأمين لسياسة معينة، بالسنوات.
تكرار المطالبات هو عدد المطالبات مقسومًا على التعرض، يتم قياسه عادةً بعدد المطالبات في السنة.
في هذه المجموعة من البيانات، يتوافق كل عينة مع سياسة تأمين. تتضمن الميزات المتوفرة عمر السائق وعمر المركبة وقوة المركبة، إلخ.
هدفنا هو التنبؤ بالتردد المتوقع للمطالبات بعد حوادث السيارات لحامل وثيقة تأمين جديدة بالنظر إلى البيانات التاريخية على سكان حاملي وثائق التأمين.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
مجموعة بيانات مطالبات السيارات الفرنسية#
دعنا نحمل مجموعة بيانات المطالبات من OpenML: https://www.openml.org/d/41214
from sklearn.datasets import fetch_openml
df = fetch_openml(data_id=41214, as_frame=True).frame
df
عدد المطالبات (ClaimNb) هو عدد صحيح إيجابي يمكن نمذجته
كتوزيع بواسون. يفترض بعد ذلك أن يكون عدد الأحداث المنفصلة
التي تحدث بمعدل ثابت في فترة زمنية معينة (Exposure،
بوحدات السنوات).
هنا نريد نمذجة التردد y = ClaimNb / Exposure شرطياً
على X عبر توزيع بواسون (مقياس)، واستخدام Exposure كـ
sample_weight.
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
print("متوسط التردد = {}".format(np.average(df["Frequency"], weights=df["Exposure"])))
print("نسبة التعرض بدون مطالبات = {0:.1%}".format(
df.loc[df["ClaimNb"] == 0, "Exposure"].sum() / df["Exposure"].sum()
))
fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(16, 4))
ax0.set_title("عدد المطالبات")
_ = df["ClaimNb"].hist(bins=30, log=True, ax=ax0)
ax1.set_title("التعرض بالسنوات")
_ = df["Exposure"].hist(bins=30, log=True, ax=ax1)
ax2.set_title("التردد (عدد المطالبات في السنة)")
_ = df["Frequency"].hist(bins=30, log=True, ax=ax2)
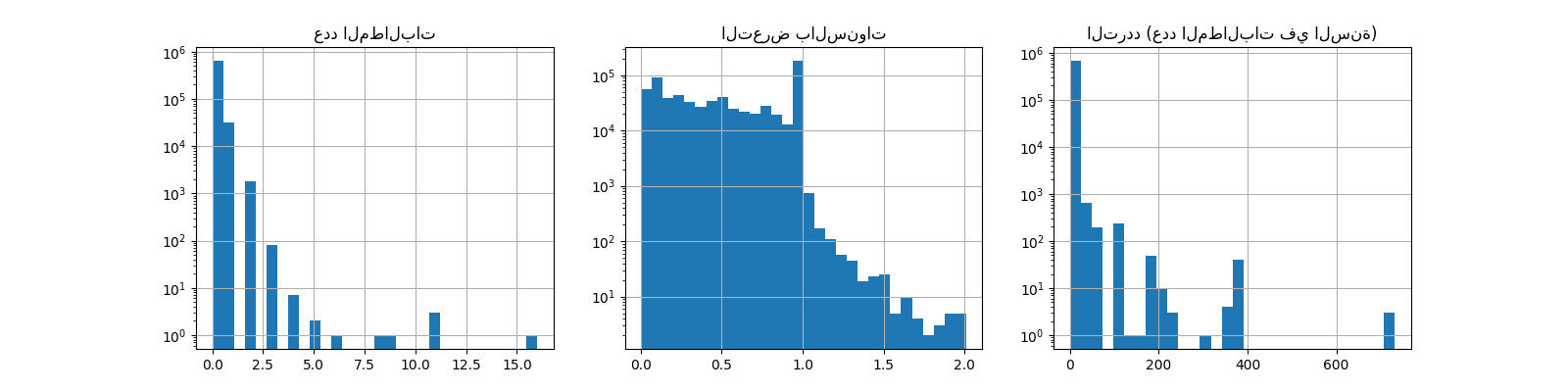
متوسط التردد = 0.10070308464041304
نسبة التعرض بدون مطالبات = 93.9%
يمكن استخدام الأعمدة المتبقية للتنبؤ بتردد أحداث المطالبات. هذه الأعمدة غير متجانسة للغاية مع مزيج من المتغيرات الفئوية والرقمية بمقاييس مختلفة، ربما موزعة بشكل غير متساوٍ للغاية.
من أجل تركيب نماذج خطية مع هذه المتنبئات، من الضروري لذلك من الضروري إجراء تحويلات ميزات قياسية كما يلي:
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
FunctionTransformer,
KBinsDiscretizer,
OneHotEncoder,
StandardScaler,
)
log_scale_transformer = make_pipeline(
FunctionTransformer(np.log, validate=False), StandardScaler()
)
linear_model_preprocessor = ColumnTransformer(
[
("passthrough_numeric", "passthrough", ["BonusMalus"]),
(
"binned_numeric",
KBinsDiscretizer(n_bins=10, random_state=0),
["VehAge", "DrivAge"],
),
("log_scaled_numeric", log_scale_transformer, ["Density"]),
(
"onehot_categorical",
OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"],
),
],
remainder="drop",
)
خط أساس تنبؤ ثابت#
تجدر الإشارة إلى أن أكثر من 93% من حاملي وثائق التأمين ليس لديهم مطالبات. إذا كنا سنحول هذه المشكلة إلى مهمة تصنيف ثنائي، فستكون غير متوازن بشكل كبير، وحتى نموذج بسيط يتنبأ فقط يمكن أن يحقق متوسط دقة 93%.
لتقييم ملاءمة المقاييس المستخدمة، سننظر في خط أساس "غبي" مقدر يتنبأ باستمرار بمتوسط تردد عينة التدريب.
from sklearn.dummy import DummyRegressor
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
df_train, df_test = train_test_split(df, test_size=0.33, random_state=0)
dummy = Pipeline(
[
("preprocessor", linear_model_preprocessor),
("regressor", DummyRegressor(strategy="mean")),
]
).fit(df_train, df_train["Frequency"], regressor__sample_weight=df_train["Exposure"])
دعنا نحسب أداء هذا خط الأساس للتنبؤ الثابت مع 3 مقاييس الانحدار المختلفة:
from sklearn.metrics import (
mean_absolute_error,
mean_poisson_deviance,
mean_squared_error,
)
def score_estimator(estimator, df_test):
"""Score an estimator on the test set."""
y_pred = estimator.predict(df_test)
print( "MSE: %.3f"
% mean_squared_error(
df_test["Frequency"], y_pred, sample_weight=df_test["Exposure"]
))
print( "MAE: %.3f"
% mean_absolute_error(
df_test["Frequency"], y_pred, sample_weight=df_test["Exposure"]
))
# تجاهل التوقعات غير الإيجابية، لأنها غير صالحة لـ
# انحراف بواسون.
mask = y_pred > 0
if (~mask).any():
n_masked, n_samples = (~mask).sum(), mask.shape[0]
print( "تحذير: يُرجى إرجاع المُقدر تنبؤات غير صالحة، غير إيجابية "
f" لـ {n_masked} عينات من {n_samples}. يتم تجاهل هذه التوقعات "
"عند حساب انحراف بواسون.")
print( "متوسط انحراف بواسون: %.3f"
% mean_poisson_deviance(
df_test["Frequency"][mask],
y_pred[mask],
sample_weight=df_test["Exposure"][mask],
))
print("تقييم تردد متوسط ثابت:")
score_estimator(dummy, df_test)
تقييم تردد متوسط ثابت:
MSE: 0.564
MAE: 0.189
متوسط انحراف بواسون: 0.625
نماذج (عامة) خطية#
نبدأ بنمذجة المتغير الهدف مع نموذج الانحدار الخطي الأقل تربيعًا (L2)،
المعروف أكثر as الانحدار المحدب. نحن
استخدام عقوبة منخفضة alpha، حيث نتوقع أن هذا النموذج الخطي
ليتناسب مع هذه المجموعة الكبيرة من البيانات.
لا يمكن حساب انحراف بواسون على القيم غير الإيجابية التي تنبأ بها
النموذج. بالنسبة للنماذج التي تعيد عددًا قليلاً من التوقعات غير الإيجابية (على سبيل المثال
Ridge) نتجاهل العينات المقابلة،
بمعنى أن انحراف بواسون المحسوب هو تقريبي. يمكن أن يكون النهج البديل
لاستخدام TransformedTargetRegressor
ميتا المقدر لتعيين y_pred إلى مجال إيجابي صارم.
print("تقييم Ridge:")
score_estimator(ridge_glm, df_test)
تقييم Ridge:
MSE: 0.560
MAE: 0.186
تحذير: يُرجى إرجاع المُقدر تنبؤات غير صالحة، غير إيجابية لـ 595 عينات من 223745. يتم تجاهل هذه التوقعات عند حساب انحراف بواسون.
متوسط انحراف بواسون: 0.597
بعد ذلك، نقوم بتركيب المُرجع بواسون على المتغير الهدف. نحن نحدد
قوة التنظيم alpha إلى ما يقرب من 1e-6 على عدد
العينات (أي 1e-12) لمحاكاة المُرجع المحدب الذي يختلف L2
مصطلح العقوبة بشكل مختلف مع عدد العينات.
نظرًا لأن المُرجع بواسون يقوم داخليًا بنمذجة سجل القيمة المستهدفة المتوقعة بدلاً من القيمة المتوقعة مباشرة (رابط تسجيل الدخول مقابل رابط الهوية)، العلاقة بين X و y لم تعد خطية تمامًا. لذلك يطلق على المُرجع بواسون نموذج خطي عام (GLM) بدلاً من نموذج خطي عادي كما هو الحال مع الانحدار المحدب.
from sklearn.linear_model import PoissonRegressor
n_samples = df_train.shape[0]
poisson_glm = Pipeline(
[
("preprocessor", linear_model_preprocessor),
("regressor", PoissonRegressor(alpha=1e-12, solver="newton-cholesky")),
]
)
poisson_glm.fit(
df_train, df_train["Frequency"], regressor__sample_weight=df_train["Exposure"]
)
print("تقييم PoissonRegressor:")
score_estimator(poisson_glm, df_test)
تقييم PoissonRegressor:
MSE: 0.560
MAE: 0.186
متوسط انحراف بواسون: 0.594
أشجار تعزيز التدرج للانحدار بواسون#
أخيرًا، سنأخذ في الاعتبار نموذجًا غير خطي، وهو أشجار تعزيز التدرج. لا تتطلب النماذج الشجرية
أن تكون البيانات الفئوية مشفرة بترميز أحادي الساخن: بدلاً من ذلك، يمكننا ترميز كل
تسمية الفئة برقم عشوائي باستخدام OrdinalEncoder. مع هذا
الترميز، ستعامل الأشجار الميزات الفئوية كميزات مرتبة، والتي قد لا تكون
سلوك مرغوب فيه دائمًا. ومع ذلك، فإن هذا التأثير محدود
بالنسبة للأشجار العميقة بما يكفي لاستعادة الطبيعة الفئوية
الميزات. الميزة الرئيسية لـ
OrdinalEncoder على
OneHotEncoder هو أنه سيجعل التدريب
أسرع.
يوفر تعزيز التدرج أيضًا إمكانية تركيب الأشجار بخسارة بواسون (مع رابط تسجيل الدخول الضمني) بدلاً من خسارة المربعات الأقل الافتراضية. هنا نحن فقط تركيب الأشجار بخسارة بواسون للحفاظ على هذا المثال موجز.
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.preprocessing import OrdinalEncoder
tree_preprocessor = ColumnTransformer(
[
(
"categorical",
OrdinalEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"],
),
("numeric", "passthrough", ["VehAge", "DrivAge", "BonusMalus", "Density"]),
],
remainder="drop",
)
poisson_gbrt = Pipeline(
[
("preprocessor", tree_preprocessor),
(
"regressor",
HistGradientBoostingRegressor(loss="poisson", max_leaf_nodes=128),
),
]
)
poisson_gbrt.fit(
df_train, df_train["Frequency"], regressor__sample_weight=df_train["Exposure"]
)
print("تقييم أشجار تعزيز التدرج بواسون:")
score_estimator(poisson_gbrt, df_test)
تقييم أشجار تعزيز التدرج بواسون:
MSE: 0.559
MAE: 0.184
متوسط انحراف بواسون: 0.575
مثل GLM بواسون أعلاه، يقلل نموذج الأشجار المعززة التدرج انحراف بواسون. ومع ذلك، بسبب قوة تنبؤية أعلى، يصل إلى قيم أقل من انحراف بواسون.
تقييم النماذج بتقسيم تدريب / اختبار واحد عرضة للتقلبات العشوائية. إذا تسمح موارد الكمبيوتر، يجب التحقق من أن المقاييس المتقاطعة من شأنه أن يؤدي إلى استنتاجات مماثلة.
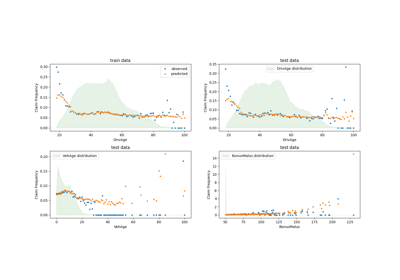
يمكن أيضًا تصور الاختلاف النوعي بين هذه النماذج عن طريق مقارنة مخطط توزيع القيم المستهدفة الملاحظة بذلك من القيم المتوقعة:
fig, axes = plt.subplots(nrows=2, ncols=4, figsize=(16, 6), sharey=True)
fig.subplots_adjust(bottom=0.2)
n_bins = 20
for row_idx, label, df in zip(range(2), ["train", "test"], [df_train, df_test]):
df["Frequency"].hist(bins=np.linspace(-1, 30, n_bins), ax=axes[row_idx, 0])
axes[row_idx, 0].set_title("Data")
axes[row_idx, 0].set_yscale("log")
axes[row_idx, 0].set_xlabel("y (التردد الملاحظ)")
axes[row_idx, 0].set_ylim([1e1, 5e5])
axes[row_idx, 0].set_ylabel(label + " samples")
for idx, model in enumerate([ridge_glm, poisson_glm, poisson_gbrt]):
y_pred = model.predict(df)
pd.Series(y_pred).hist(
bins=np.linspace(-1, 4, n_bins), ax=axes[row_idx, idx + 1]
)
axes[row_idx, idx + 1].set(
title=model[-1].__class__.__name__,
yscale="log",
xlabel="y_pred (التردد المتوقع المتوقع)",
)
plt.tight_layout()
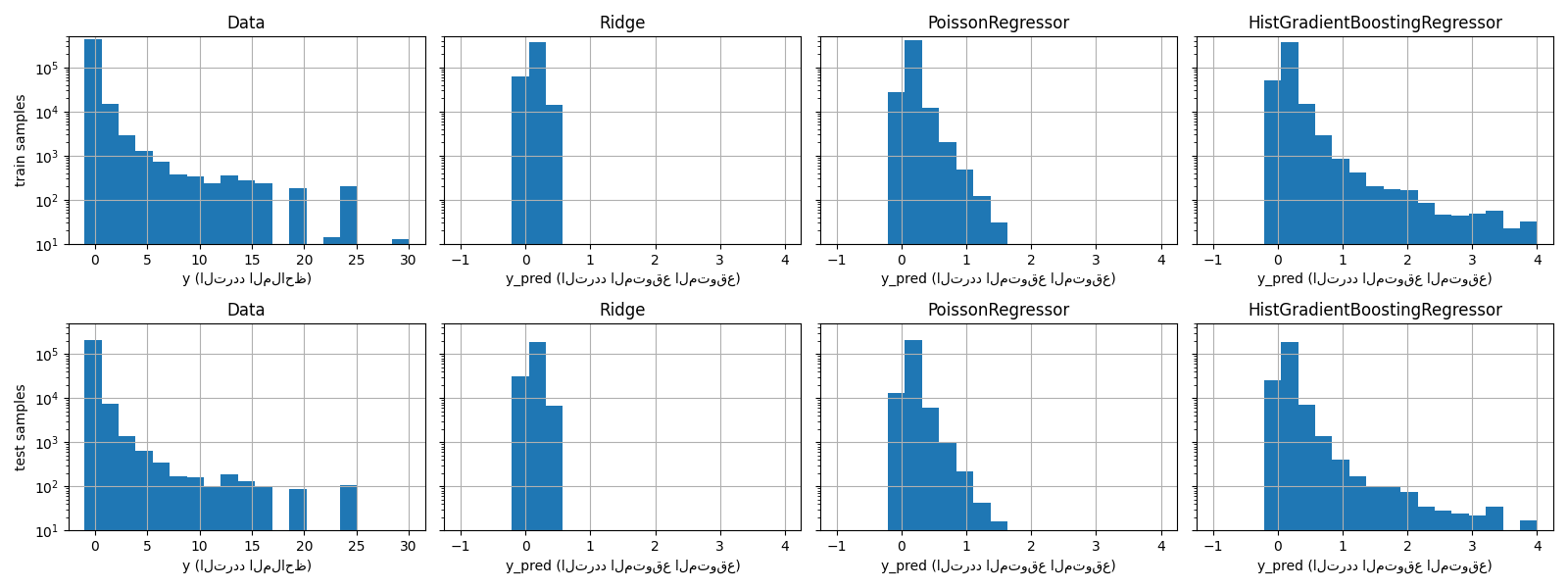
تعرض البيانات التجريبية توزيع ذيل طويل لـ y. في جميع
النماذج، نتوقع التردد المتوقع لمتغير عشوائي، لذلك سنكون
بالضرورة قيم متطرفة أقل من تلك الخاصة
إدراكات هذا المتغير العشوائي. هذا يفسر أن وضع مخطط توزيع
تنبؤات النموذج لا تتوافق بالضرورة مع القيمة الأصغر.
بالإضافة إلى ذلك، فإن التوزيع الطبيعي المستخدم في Ridge له
تباين ثابت، في حين أن توزيع بواسون المستخدم في PoissonRegressor و
HistGradientBoostingRegressor، التباين يتناسب مع
القيمة المتوقعة المتوقعة.
وبالتالي، من بين المقدرات التي تم النظر فيها، PoissonRegressor و
HistGradientBoostingRegressor هي مسبقًا أفضل ملاءمة لنمذجة
توزيع ذيل طويل للبيانات غير السلبية مقارنةً بنموذج Ridge الذي
يفترض افتراضًا خاطئًا على توزيع المتغير الهدف.
المقدر HistGradientBoostingRegressor لديه أكبر قدر من المرونة
ويمكنه التنبؤ بقيم متوقعة أعلى.
تجدر الإشارة إلى أننا كنا قد استخدمنا خسارة المربعات الأقل لـ
نموذج HistGradientBoostingRegressor. هذا من شأنه أن يفترض خطأً
توزيع
Total running time of the script: (0 minutes 15.067 seconds)
Related examples