ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
فترات التنبؤ لانحدار التعزيز المتدرج#
يوضح هذا المثال كيفية استخدام انحدار الكميات لإنشاء فترات تنبؤ. انظر الميزات في أشجار التعزيز المتدرج للهيستوغرام
لمثال يعرض بعض الميزات الأخرى لـ
HistGradientBoostingRegressor.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
إنشاء بعض البيانات لمشكلة انحدار اصطناعية عن طريق تطبيق الدالة f على مدخلات عشوائية موزعة بشكل منتظم.
from sklearn.base import clone
from pprint import pprint
from sklearn.metrics import make_scorer
from sklearn.model_selection import HalvingRandomSearchCV
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_pinball_loss, mean_squared_error
from sklearn.ensemble import GradientBoostingRegressor
import numpy as np
from sklearn.model_selection import train_test_split
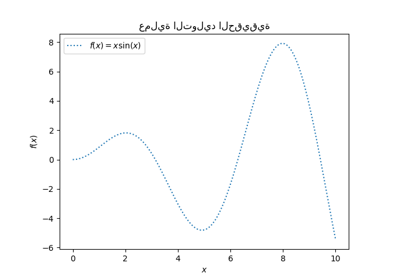
def f(x):
"""الدالة المراد التنبؤ بها."""
return x * np.sin(x)
rng = np.random.RandomState(42)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
لجعل المشكلة مثيرة للاهتمام، نقوم بإنشاء ملاحظات للهدف y على أنها مجموع حد حتمي محسوب بواسطة الدالة f وحد ضوضاء عشوائي يتبع توزيع لوغاريتمي عادي متمركز. لجعل هذا أكثر إثارة للاهتمام، نأخذ في الاعتبار الحالة التي يعتمد فيها اتساع الضوضاء على المتغير المدخل x (ضوضاء غير متجانسة).
التوزيع اللوغاريتمي العادي غير متماثل وذو ذيل طويل: من المحتمل ملاحظة قيم متطرفة كبيرة ولكن من المستحيل ملاحظة قيم متطرفة صغيرة.
sigma = 0.5 + X.ravel() / 10
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2 / 2)
y = expected_y + noise
تقسيم البيانات إلى مجموعات تدريب واختبار:
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
ملاءمة منحنيات انحدار كمية وغير خطية للمربعات الصغرى#
ملاءمة نماذج التعزيز المتدرج المدربة مع خسارة الكمية و alpha=0.05، 0.5، 0.95.
النماذج التي تم الحصول عليها لـ alpha=0.05 و alpha=0.95 تنتج فاصل ثقة 90% (95% - 5% = 90%).
النموذج المدرب بـ alpha=0.5 ينتج انحدارًا للوسيط: في المتوسط، يجب أن يكون هناك نفس عدد ملاحظات الهدف فوق وتحت القيم المتوقعة.
all_models = {}
common_params = dict(
learning_rate=0.05,
n_estimators=200,
max_depth=2,
min_samples_leaf=9,
min_samples_split=9,
)
for alpha in [0.05, 0.5, 0.95]:
gbr = GradientBoostingRegressor(
loss="quantile", alpha=alpha, **common_params)
all_models["q %1.2f" % alpha] = gbr.fit(X_train, y_train)
لاحظ أن HistGradientBoostingRegressor أسرع بكثير من
GradientBoostingRegressor بدءًا من
مجموعات البيانات المتوسطة (n_samples >= 10_000)، وهي ليست حالة
المثال الحالي.
من أجل المقارنة، نقوم أيضًا بملاءمة نموذج أساسي مدرب باستخدام متوسط مربع الخطأ (MSE) المعتاد.
gbr_ls = GradientBoostingRegressor(loss="squared_error", **common_params)
all_models["mse"] = gbr_ls.fit(X_train, y_train)
إنشاء مجموعة تقييم متباعدة بشكل متساوٍ من قيم الإدخال التي تغطي النطاق [0، 10].
xx = np.atleast_2d(np.linspace(0, 10, 1000)).T
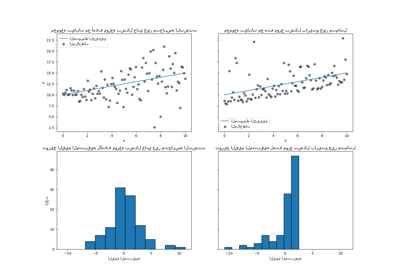
ارسم دالة المتوسط الشرطي الحقيقي f، تنبؤات المتوسط الشرطي (الخسارة تساوي مربع الخطأ)، الوسيط الشرطي وفترة 90% الشرطية (من المئين الشرطي الخامس إلى 95).
y_pred = all_models["mse"].predict(xx)
y_lower = all_models["q 0.05"].predict(xx)
y_upper = all_models["q 0.95"].predict(xx)
y_med = all_models["q 0.50"].predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "g:", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="ملاحظات الاختبار")
plt.plot(xx, y_med, "r-", label="الوسيط المتوقع")
plt.plot(xx, y_pred, "r-", label="المتوسط المتوقع")
plt.plot(xx, y_upper, "k-")
plt.plot(xx, y_lower, "k-")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="الفترة المتوقعة 90%"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.show()
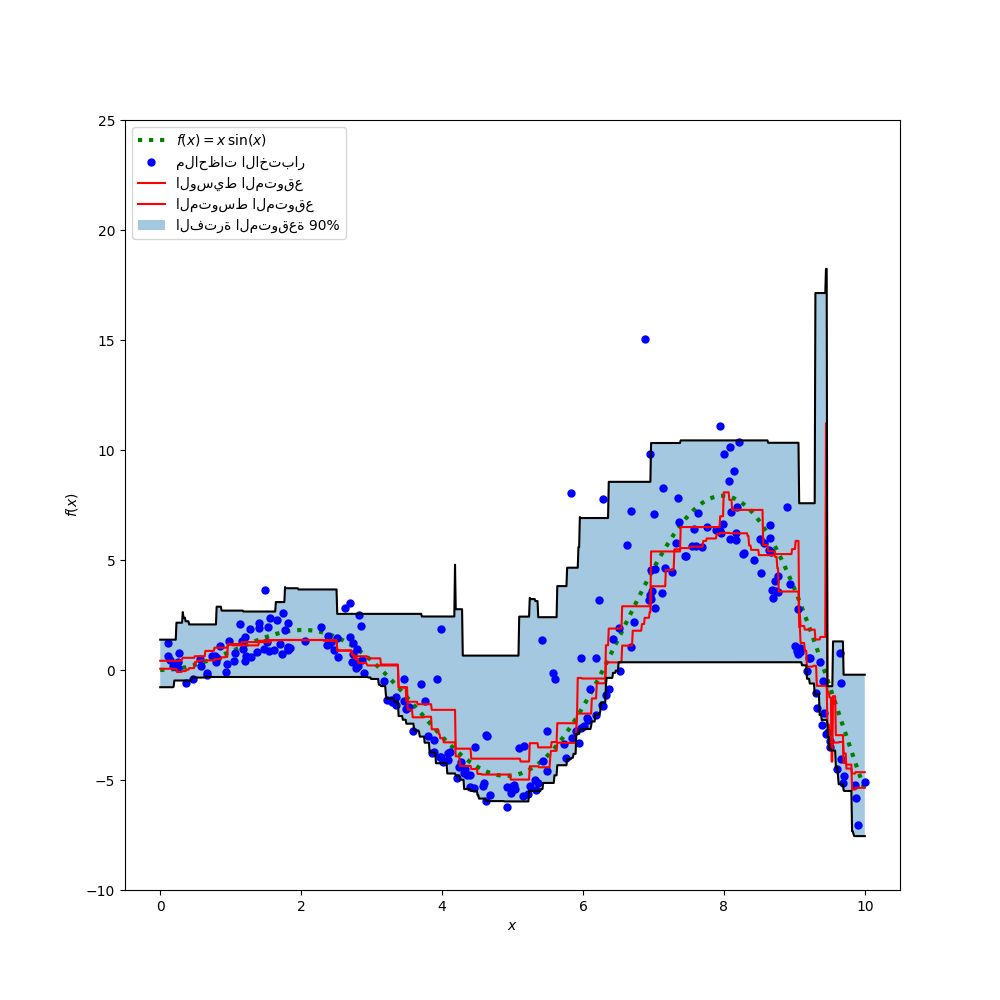
بمقارنة الوسيط المتوقع بالمتوسط المتوقع، نلاحظ أن الوسيط أقل من المتوسط في المتوسط لأن الضوضاء منحرفة نحو القيم العالية (القيم المتطرفة الكبيرة). يبدو أيضًا أن تقدير الوسيط أكثر سلاسة نظرًا لمتانته الطبيعية للقيم المتطرفة.
لاحظ أيضًا أن التحيز الاستقرائي لأشجار التعزيز المتدرج يمنع للأسف كمية 0.05 الخاصة بنا من التقاط الشكل الجيبي للإشارة بشكل كامل، خاصة حول x = 8. يمكن لضبط المعلمات الفائقة تقليل هذا التأثير كما هو موضح في الجزء الأخير من هذا الدفتر.
تحليل مقاييس الخطأ#
قياس النماذج باستخدام mean_squared_error
و mean_pinball_loss على بيانات التدريب.
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_train)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(
y_train, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_train, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
يعرض عمود واحد جميع النماذج التي تم تقييمها بواسطة نفس المقياس. يجب الحصول على الحد الأدنى للعدد في عمود عندما يتم تدريب النموذج وقياسه بنفس المقياس. يجب أن يكون هذا هو الحال دائمًا في مجموعة التدريب إذا تقارب التدريب.
لاحظ أنه نظرًا لأن توزيع الهدف غير متماثل، فإن المتوسط الشرطي المتوقع والوسيط الشرطي يختلفان اختلافًا كبيرًا، وبالتالي لا يمكن للمرء استخدام نموذج مربع الخطأ للحصول على تقدير جيد للوسيط الشرطي أو العكس.
إذا كان توزيع الهدف متماثلًا ولم يكن به قيم متطرفة (على سبيل المثال مع ضوضاء غاوسية)، فإن مقدر الوسيط ومقدر المربعات الصغرى سينتجان تنبؤات متشابهة.
ثم نفعل الشيء نفسه في مجموعة الاختبار.
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_test)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(
y_test, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_test, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
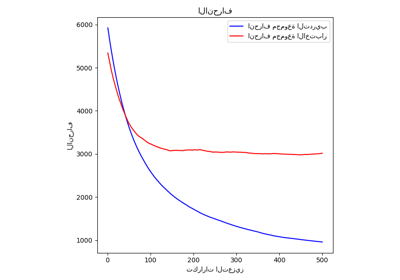
الأخطاء أعلى مما يعني أن النماذج قد تجاوزت البيانات قليلاً. لا يزال يُظهر أن أفضل مقياس اختبار يتم الحصول عليه عندما يتم تدريب النموذج عن طريق تقليل نفس المقياس.
لاحظ أن مقدر الوسيط الشرطي يتنافس مع مقدر مربع الخطأ من حيث MSE في مجموعة الاختبار: يمكن تفسير ذلك من خلال حقيقة أن مقدر مربع الخطأ حساس للغاية للقيم المتطرفة الكبيرة والتي يمكن أن تتسبب في تجاوز كبير. يمكن ملاحظة ذلك على الجانب الأيمن من الرسم البياني السابق. مقدر الوسيط الشرطي متحيز (تقليل التقدير لهذه الضوضاء غير المتماثلة) ولكنه أيضًا قوي بشكل طبيعي للقيم المتطرفة ولا يتجاوزها.
معايرة فاصل الثقة#
يمكننا أيضًا تقييم قدرة مقدري الكميات المتطرفين على إنتاج فاصل ثقة شرطي معاير جيدًا بنسبة 90%.
للقيام بذلك، يمكننا حساب جزء الملاحظات التي تقع بين التنبؤات:
def coverage_fraction(y, y_low, y_high):
return np.mean(np.logical_and(y >= y_low, y <= y_high))
coverage_fraction(
y_train,
all_models["q 0.05"].predict(X_train),
all_models["q 0.95"].predict(X_train),
)
np.float64(0.9)
في مجموعة التدريب، تكون المعايرة قريبة جدًا من قيمة التغطية المتوقعة لفاصل ثقة 90%.
coverage_fraction(
y_test, all_models["q 0.05"].predict(
X_test), all_models["q 0.95"].predict(X_test)
)
np.float64(0.868)
في مجموعة الاختبار، يكون فاصل الثقة المقدر ضيقًا جدًا. لاحظ، مع ذلك، أننا سنحتاج إلى تضمين هذه المقاييس في حلقة تحقق متقاطع لتقييم تقلبها في ظل إعادة أخذ عينات البيانات.
ضبط المعلمات الفائقة لمنحنيات انحدار الكمية#
في الرسم البياني أعلاه، لاحظنا أن منحنى انحدار المئين الخامس يبدو أنه غير مناسب ولا يمكنه التكيف مع الشكل الجيبي للإشارة.
تم ضبط المعلمات الفائقة للنموذج يدويًا تقريبًا لمنحنى انحدار الوسيط، وليس هناك سبب يدعو إلى أن تكون المعلمات الفائقة نفسها مناسبة لمنحنى انحدار المئين الخامس.
لتأكيد هذه الفرضية، نقوم بضبط المعلمات الفائقة لمنحنى انحدار جديد للمئين الخامس عن طريق تحديد أفضل معلمات النموذج عن طريق التحقق المتقاطع من خسارة الكرة والدبوس مع alpha = 0.05:
from sklearn.experimental import enable_halving_search_cv # noqa
param_grid = dict(
learning_rate=[0.05, 0.1, 0.2],
max_depth=[2, 5, 10],
min_samples_leaf=[1, 5, 10, 20],
min_samples_split=[5, 10, 20, 30, 50],
)
alpha = 0.05
neg_mean_pinball_loss_05p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # تعظيم الخسارة السلبية
)
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, random_state=0)
search_05p = HalvingRandomSearchCV(
gbr,
param_grid,
resource="n_estimators",
max_resources=250,
min_resources=50,
scoring=neg_mean_pinball_loss_05p_scorer,
n_jobs=2,
random_state=0,
).fit(X_train, y_train)
pprint(search_05p.best_params_)
{'learning_rate': 0.2,
'max_depth': 2,
'min_samples_leaf': 20,
'min_samples_split': 10,
'n_estimators': 150}
نلاحظ أن المعلمات الفائقة التي تم ضبطها يدويًا لمنحنى انحدار الوسيط تقع في نفس نطاق المعلمات الفائقة المناسبة لمنحنى انحدار المئين الخامس.
لنقم الآن بضبط المعلمات الفائقة لمنحنى انحدار المئين 95. نحتاج إلى إعادة تعريف
مقياس scoring المستخدم لتحديد أفضل نموذج، جنبًا إلى جنب مع ضبط معلمة alpha لمقدر التعزيز المتدرج الداخلي
نفسه:
alpha = 0.95
neg_mean_pinball_loss_95p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # تعظيم الخسارة السلبية
)
search_95p = clone(search_05p).set_params(
estimator__alpha=alpha,
scoring=neg_mean_pinball_loss_95p_scorer,
)
search_95p.fit(X_train, y_train)
pprint(search_95p.best_params_)
{'learning_rate': 0.05,
'max_depth': 2,
'min_samples_leaf': 5,
'min_samples_split': 20,
'n_estimators': 150}
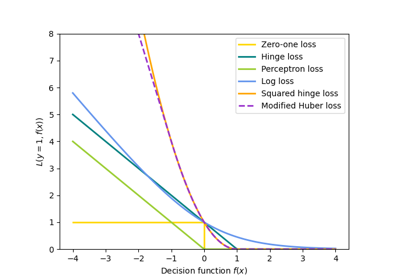
تُظهر النتيجة أن المعلمات الفائقة لمنحنى انحدار المئين 95 التي حددها إجراء البحث تقع تقريبًا في نفس نطاق المعلمات الفائقة التي تم ضبطها يدويًا لمنحنى انحدار الوسيط والمعلمات الفائقة التي حددها إجراء البحث لمنحنى انحدار المئين الخامس. ومع ذلك، أدت عمليات البحث عن المعلمات الفائقة إلى تحسين فاصل ثقة 90% الذي يتكون من تنبؤات هذين المنحنيين الكميين المضبوطين. لاحظ أن تنبؤ المئين 95 العلوي له شكل أكثر خشونة من تنبؤ المئين الخامس السفلي بسبب القيم المتطرفة:
y_lower = search_05p.predict(xx)
y_upper = search_95p.predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "g:", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="ملاحظات الاختبار")
plt.plot(xx, y_upper, "k-")
plt.plot(xx, y_lower, "k-")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="الفترة المتوقعة 90%"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.title("التنبؤ بمعلمات فائقة مضبوطة")
plt.show()
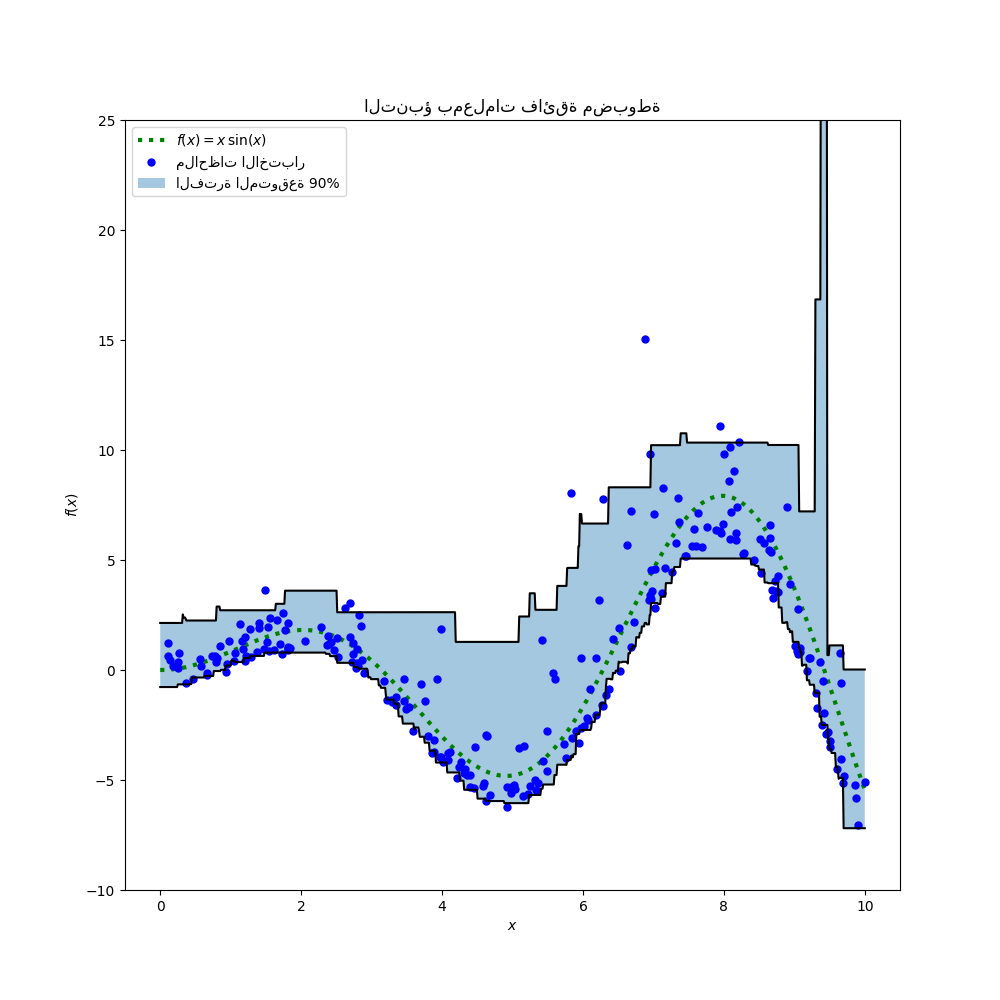
يبدو الرسم البياني نوعياً أفضل من النماذج غير المضبوطة، خاصة بالنسبة لشكل الكمية الأقل.
نقوم الآن بتقييم المعايرة المشتركة لزوج المقدرات كمياً:
coverage_fraction(y_train, search_05p.predict(
X_train), search_95p.predict(X_train))
np.float64(0.9026666666666666)
coverage_fraction(y_test, search_05p.predict(
X_test), search_95p.predict(X_test))
np.float64(0.796)
معايرة الزوج المضبوط للأسف ليست أفضل في مجموعة الاختبار: لا يزال عرض فاصل الثقة المقدر ضيقًا جدًا.
مرة أخرى، سنحتاج إلى تضمين هذه الدراسة في حلقة تحقق متقاطع لتقييم تقلب هذه التقديرات بشكل أفضل.
Total running time of the script: (0 minutes 12.069 seconds)
Related examples