ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

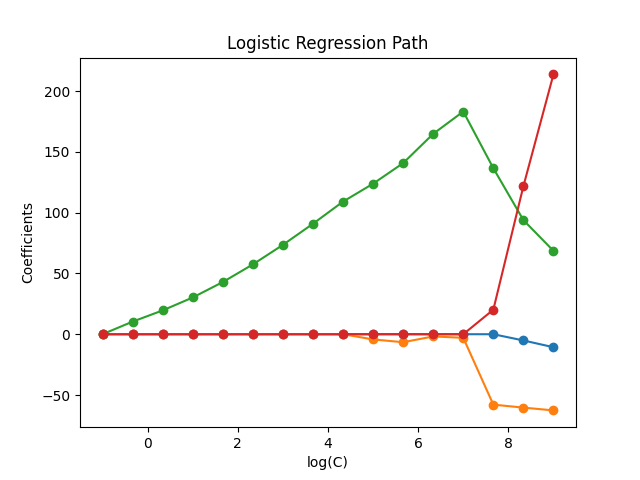
مسار التنظيم لـ L1 - الانحدار اللوجستي#

قم بتدريب نماذج الانحدار اللوجستي المنتظمة بـ L1 على مشكلة تصنيف ثنائي مستمدة من مجموعة بيانات Iris.

تم ترتيب النماذج من الأكثر تنظيماً إلى الأقل تنظيماً. تم جمع المعاملات الأربعة للنماذج وتم رسمها كـ "مسار تنظيم": على الجانب الأيسر من الشكل (المنظمون الأقوياء)، جميع المعاملات تساوي بالضبط 0. عندما يصبح التنظيم تدريجياً أكثر مرونة، يمكن للمعاملات الحصول على قيم غير صفرية واحدة تلو الأخرى.

هنا نختار محدد liblinear لأنه يمكنه تحسين خسارة الانحدار اللوجستي بكفاءة مع عقوبة L1 غير الملساء، والتي تحفز على التباعد.

لاحظ أيضاً أننا نحدد قيمة منخفضة للتسامح للتأكد من أن النموذج قد تقارب قبل جمع المعاملات.

نستخدم أيضاً warm_start=True مما يعني أن معاملات النماذج يتم إعادة استخدامها لتهيئة النموذج التالي لتسريع حساب المسار الكامل.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

تحميل البيانات#

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 2]
y = y[y != 2]

X /= X.max()  # تطبيع X لتسريع التقارب

حساب مسار التنظيم#

import numpy as np

from sklearn import linear_model
from sklearn.svm import l1_min_c

cs = l1_min_c(X, y, loss="log") * np.logspace(0, 10, 16)

clf = linear_model.LogisticRegression(
    penalty="l1",
    solver="liblinear",
    tol=1e-6,
    max_iter=int(1e6),
    warm_start=True,
    intercept_scaling=10000.0,
)
coefs_ = []
for c in cs:
    clf.set_params(C=c)
    clf.fit(X, y)
    coefs_.append(clf.coef_.ravel().copy())

coefs_ = np.array(coefs_)

رسم مسار التنظيم#

import matplotlib.pyplot as plt

plt.plot(np.log10(cs), coefs_, marker="o")
ymin, ymax = plt.ylim()
plt.xlabel("log(C)")
plt.ylabel("Coefficients")
plt.title("Logistic Regression Path")
plt.axis("tight")
plt.show()