ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
الانحدار اللوجستي المتناثر متعدد الفئات على 20newgroups#
مقارنة الانحدار اللوجستي متعدد الحدود L1 مقابل الانحدار اللوجستي واحد مقابل البقية L1 لتصنيف المستندات من مجموعة بيانات newgroups20. ينتج الانحدار اللوجستي متعدد الحدود نتائج أكثر دقة وهو أسرع في التدريب على مجموعة البيانات الأكبر حجمًا.
هنا نستخدم التناثر l1 الذي يقلص أوزان الميزات غير المفيدة إلى الصفر. هذا جيد إذا كان الهدف هو استخراج المفردات التمييزية القوية لكل فئة. إذا كان الهدف هو الحصول على أفضل دقة تنبؤية، فمن الأفضل استخدام عقوبة l2 غير المسببة للتناثر بدلاً من ذلك.
هناك طريقة أكثر تقليدية (وربما أفضل) للتنبؤ على مجموعة فرعية متناثرة من ميزات الإدخال وهي استخدام اختيار الميزات أحادي المتغير متبوعًا بنموذج انحدار لوجستي تقليدي (معاقب بـ l2).
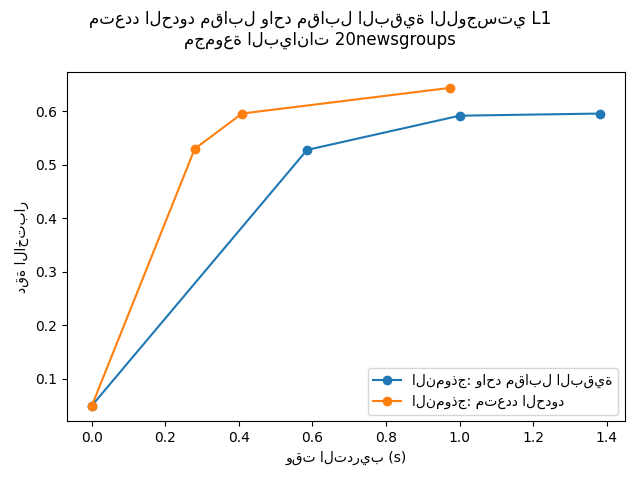
مجموعة بيانات 20newsgroup، train_samples=4500، n_features=130107، n_classes=20
[model=واحد مقابل البقية, solver=saga] عدد العهود: 1
[model=واحد مقابل البقية, solver=saga] عدد العهود: 2
[model=واحد مقابل البقية, solver=saga] عدد العهود: 3
دقة الاختبار للنموذج ovr: 0.5960
% معاملات غير صفرية للنموذج ovr، لكل فئة:
[0.26593496 0.43348936 0.26362917 0.31973683 0.37815029 0.2928359
0.27054655 0.62717609 0.19522393 0.30897646 0.34586917 0.28207552
0.34125758 0.29898468 0.34279478 0.59489497 0.38353048 0.35278655
0.19829832 0.14603365]
وقت التشغيل (3 عهود) للنموذج ovr:1.38
[model=متعدد الحدود, solver=saga] عدد العهود: 1
[model=متعدد الحدود, solver=saga] عدد العهود: 2
[model=متعدد الحدود, solver=saga] عدد العهود: 5
دقة الاختبار للنموذج multinomial: 0.6440
% معاملات غير صفرية للنموذج multinomial، لكل فئة:
[0.36047253 0.1268187 0.10606655 0.17985197 0.5395559 0.07993421
0.06686804 0.21443888 0.11528972 0.2075215 0.10914094 0.11144673
0.13988486 0.09684337 0.26286057 0.11682692 0.55800226 0.17370318
0.11452112 0.14603365]
وقت التشغيل (5 عهود) للنموذج multinomial:0.97
تم تشغيل المثال في 27.860 s
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import timeit
import warnings
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_20newsgroups_vectorized
from sklearn.exceptions import ConvergenceWarning
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.multiclass import OneVsRestClassifier
warnings.filterwarnings("ignore", category=ConvergenceWarning, module="sklearn")
t0 = timeit.default_timer()
# نحن نستخدم مُحل SAGA
solver = "saga"
# قلل من أجل وقت تشغيل أسرع
n_samples = 5000
X, y = fetch_20newsgroups_vectorized(subset="all", return_X_y=True)
X = X[:n_samples]
y = y[:n_samples]
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=42, stratify=y, test_size=0.1
)
train_samples, n_features = X_train.shape
n_classes = np.unique(y).shape[0]
print(
"مجموعة بيانات 20newsgroup، train_samples=%i، n_features=%i، n_classes=%i"
% (train_samples, n_features, n_classes)
)
models = {
"ovr": {"name": "واحد مقابل البقية", "iters": [1, 2, 3]},
"multinomial": {"name": "متعدد الحدود", "iters": [1, 2, 5]},
}
for model in models:
# إضافة قيم مستوى الفرصة الأولية لأغراض الرسم
accuracies = [1 / n_classes]
times = [0]
densities = [1]
model_params = models[model]
# عدد قليل من العهود لوقت تشغيل سريع
for this_max_iter in model_params["iters"]:
print(
"[model=%s, solver=%s] عدد العهود: %s"
% (model_params["name"], solver, this_max_iter)
)
clf = LogisticRegression(
solver=solver,
penalty="l1",
max_iter=this_max_iter,
random_state=42,
)
if model == "ovr":
clf = OneVsRestClassifier(clf)
t1 = timeit.default_timer()
clf.fit(X_train, y_train)
train_time = timeit.default_timer() - t1
y_pred = clf.predict(X_test)
accuracy = np.sum(y_pred == y_test) / y_test.shape[0]
if model == "ovr":
coef = np.concatenate([est.coef_ for est in clf.estimators_])
else:
coef = clf.coef_
density = np.mean(coef != 0, axis=1) * 100
accuracies.append(accuracy)
densities.append(density)
times.append(train_time)
models[model]["times"] = times
models[model]["densities"] = densities
models[model]["accuracies"] = accuracies
print("دقة الاختبار للنموذج %s: %.4f" % (model, accuracies[-1]))
print(
"%% معاملات غير صفرية للنموذج %s، لكل فئة:\n %s"
% (model, densities[-1])
)
print(
"وقت التشغيل (%i عهود) للنموذج %s:%.2f"
% (model_params["iters"][-1], model, times[-1])
)
fig = plt.figure()
ax = fig.add_subplot(111)
for model in models:
name = models[model]["name"]
times = models[model]["times"]
accuracies = models[model]["accuracies"]
ax.plot(times, accuracies, marker="o", label="النموذج: %s" % name)
ax.set_xlabel("وقت التدريب (s)")
ax.set_ylabel("دقة الاختبار")
ax.legend()
fig.suptitle(
"متعدد الحدود مقابل واحد مقابل البقية اللوجستي L1\nمجموعة البيانات %s" % "20newsgroups"
)
fig.tight_layout()
fig.subplots_adjust(top=0.85)
run_time = timeit.default_timer() - t0
print("تم تشغيل المثال في %.3f s" % run_time)
plt.show()
Total running time of the script: (0 minutes 27.934 seconds)
Related examples
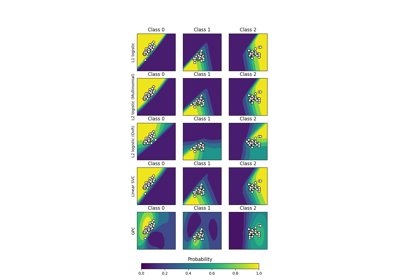
حدود القرار للانحدار متعدد الحدود والانحدار اللوجستي من النوع واحد مقابل البقية