ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

# مقارنة المنحنيات الخطية للانحدار البايزي#

يقارن هذا المثال بين طريقتين مختلفتين للانحدار البايزي:

في الجزء الأول، نستخدم نموذج المربعات الصغرى العادية (OLS) كخط أساس لمقارنة معاملات النماذج فيما يتعلق بالمعاملات الحقيقية. بعد ذلك، نوضح أن تقدير مثل هذه النماذج يتم عن طريق زيادة تسجيل الاحتمال الهامشي للملاحظات بشكل تكراري.

في القسم الأخير، نرسم التنبؤات وعدم اليقين لكل من الانحدار البايزي والانحدار الخطي باستخدام توسيع الميزات متعددة الحدود لتناسب العلاقة غير الخطية بين X و y.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

متانة النماذج لاستعادة الأوزان الحقيقية#

توليد مجموعة بيانات صناعية#

نقوم بتوليد مجموعة بيانات حيث X و y مرتبطان خطيًا: 10 من ميزات X سيتم استخدامها لتوليد y. الميزات الأخرى ليست مفيدة في التنبؤ بـ y. بالإضافة إلى ذلك، نقوم بتوليد مجموعة بيانات حيث n_samples == n_features. مثل هذا الإعداد يمثل تحديًا لنموذج OLS وقد يؤدي إلى أوزان كبيرة بشكل تعسفي. وجود تقدير مسبق للأوزان وعقوبة يخفف من المشكلة. وأخيرًا، تتم إضافة ضجيج غاوسي.

from sklearn.datasets import make_regression

X, y, true_weights = make_regression(
    n_samples=100,
    n_features=100,
    n_informative=10,
    noise=8,
    coef=True,
    random_state=42,
)

ملاءمة المنحنيات#

نقوم الآن بملاءمة كلا النموذجين البايزيين ونموذج OLS لمقارنة معاملات النماذج لاحقًا.

import pandas as pd

from sklearn.linear_model import ARDRegression, BayesianRidge, LinearRegression

olr = LinearRegression().fit(X, y)
brr = BayesianRidge(compute_score=True, max_iter=30).fit(X, y)
ard = ARDRegression(compute_score=True, max_iter=30).fit(X, y)
df = pd.DataFrame(
    {
        "Weights of true generative process": true_weights,
        "ARDRegression": ard.coef_,
        "BayesianRidge": brr.coef_,
        "LinearRegression": olr.coef_,
    }
)

رسم المعاملات الحقيقية والمقدرة#

نقارن الآن معاملات كل نموذج بأوزان النموذج التوليدي الحقيقي.

import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import SymLogNorm

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-80, vmax=80),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.tight_layout(rect=(0, 0, 1, 0.95))
_ = plt.title("Models' coefficients")

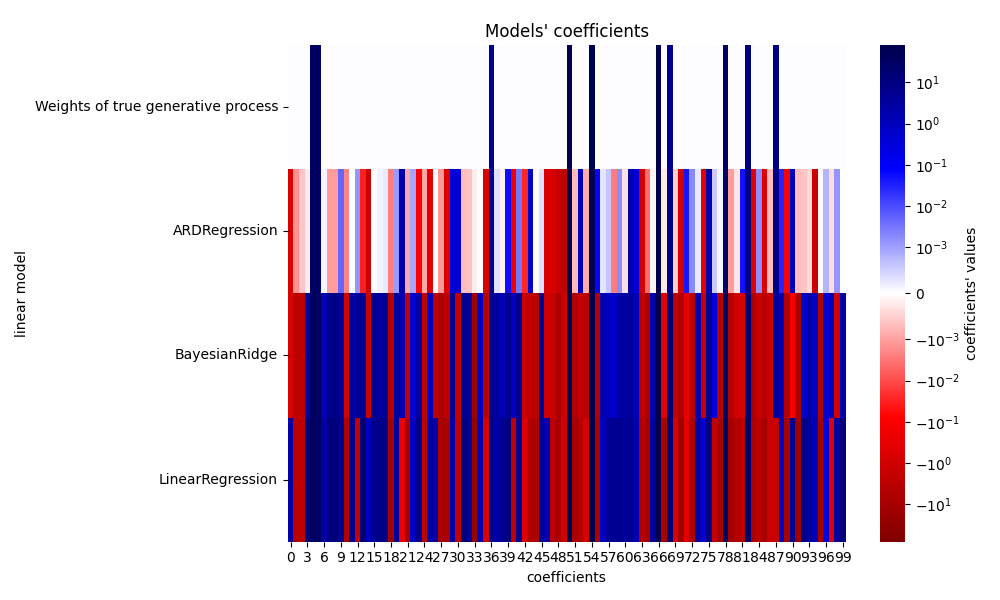
بسبب الضجيج المُضاف، لا يستعيد أي من النماذج الأوزان الحقيقية. في الواقع،: جميع النماذج لديها دائمًا أكثر من 10 معاملات غير صفرية. مقارنة بمقدر OLS
، فإن المعاملات باستخدام الانحدار البايزي متعدد الحدود تتحول قليلاً: نحو الصفر، مما يجعلها أكثر استقرارًا. يوفر الانحدار البايزي متعدد الحدود حلاً أكثر ندرة: يتم تعيين بعض المعاملات غير المعلوماتية بدقة إلى الصفر، في حين أن البعض الآخر أقرب إلى الصفر. لا تزال بعض المعاملات غير المعلوماتية موجودة وتحتفظ بقيم كبيرة.

رسم تسجيل الاحتمال الهامشي#

import numpy as np

ard_scores = -np.array(ard.scores_)
brr_scores = -np.array(brr.scores_)
plt.plot(ard_scores, color="navy", label="ARD")
plt.plot(brr_scores, color="red", label="BayesianRidge")
plt.ylabel("Log-likelihood")
plt.xlabel("Iterations")
plt.xlim(1, 30)
plt.legend()
_ = plt.title("Models log-likelihood")

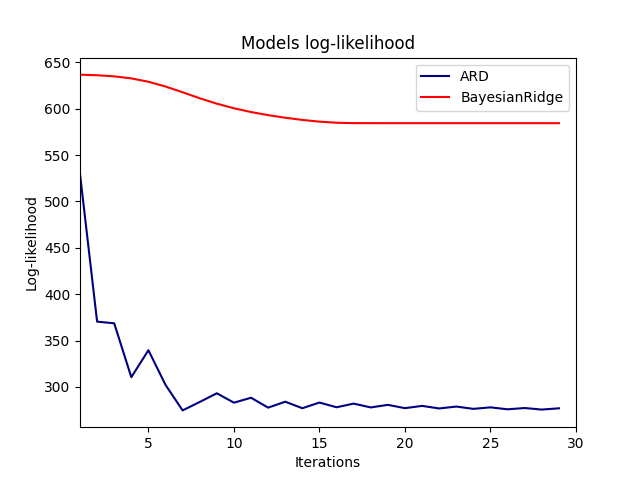
في الواقع، يقلل كلا النموذجين من تسجيل الاحتمال حتى حد تعسفي محدد بواسطة معلمة max_iter.

الانحدارات البايزية مع توسيع الميزات متعددة الحدود#

توليد مجموعة بيانات صناعية#

نقوم بإنشاء هدف يكون دالة غير خطية للميزة المدخلة. يتم إضافة ضجيج يتبع توزيع موحد قياسي.

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler

rng = np.random.RandomState(0)
n_samples = 110

# فرز البيانات لتسهيل الرسم لاحقًا
X = np.sort(-10 * rng.rand(n_samples) + 10)
noise = rng.normal(0, 1, n_samples) * 1.35
y = np.sqrt(X) * np.sin(X) + noise
full_data = pd.DataFrame({"input_feature": X, "target": y})
X = X.reshape((-1, 1))

# الاستقراء
X_plot = np.linspace(10, 10.4, 10)
y_plot = np.sqrt(X_plot) * np.sin(X_plot)
X_plot = np.concatenate((X, X_plot.reshape((-1, 1))))
y_plot = np.concatenate((y - noise, y_plot))

ملاءمة المنحنيات#

هنا نحاول استخدام متعددة حدود من الدرجة 10 لإحداث زيادة في التكيف، على الرغم من أن النماذج الخطية البايزية تنظم حجم معاملات متعددة الحدود. بما أن fit_intercept=True بشكل افتراضي لـ ARDRegression و BayesianRidge، فإن PolynomialFeatures لا يجب أن يقدم ميزة انحياز إضافية. من خلال تعيين return_std=True، فإن المنحنيات الانحدارية البايزية تعيد الانحراف المعياري لتوزيع الاحتمال اللاحق لمعاملات النموذج.

ard_poly = make_pipeline(
    PolynomialFeatures(degree=10, include_bias=False),
    StandardScaler(),
    ARDRegression(),
).fit(X, y)
brr_poly = make_pipeline(
    PolynomialFeatures(degree=10, include_bias=False),
    StandardScaler(),
    BayesianRidge(),
).fit(X, y)

y_ard, y_ard_std = ard_poly.predict(X_plot, return_std=True)
y_brr, y_brr_std = brr_poly.predict(X_plot, return_std=True)

رسم الانحدارات متعددة الحدود مع أخطاء معايير الدرجات#

ax = sns.scatterplot(
    data=full_data, x="input_feature", y="target", color="black", alpha=0.75
)
ax.plot(X_plot, y_plot, color="black", label="Ground Truth")
ax.plot(X_plot, y_brr, color="red", label="BayesianRidge with polynomial features")
ax.plot(X_plot, y_ard, color="navy", label="ARD with polynomial features")
ax.fill_between(
    X_plot.ravel(),
    y_ard - y_ard_std,
    y_ard + y_ard_std,
    color="navy",
    alpha=0.3,
)
ax.fill_between(
    X_plot.ravel(),
    y_brr - y_brr_std,
    y_brr + y_brr_std,
    color="red",
    alpha=0.3,
)
ax.legend()
_ = ax.set_title("Polynomial fit of a non-linear feature")

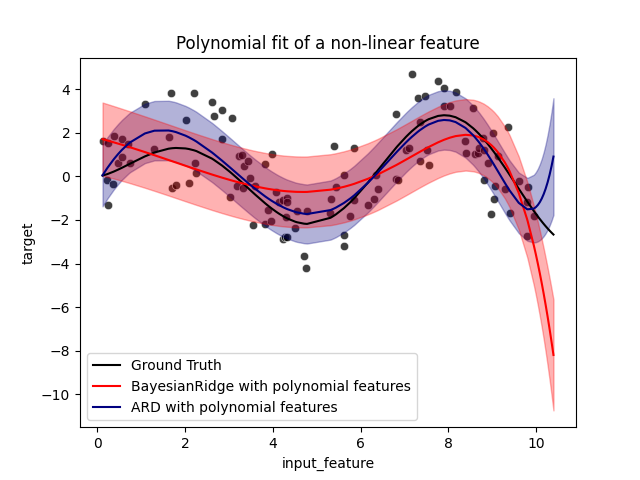
تمثل أشرطة الخطأ انحرافًا معياريًا واحدًا للتوزيع الغاوسي نقاط الاستعلام. لاحظ أن الانحدار البايزي متعدد الحدود يلتقط الحقيقة الأرضية على أفضل وجه عند استخدام المعلمات الافتراضية في كلا النموذجين، ولكن تقليل معلمة lambda_init للانحدار البايزي متعدد الحدود يمكن أن يقلل من تحيزه (انظر المثال sphx_glr_auto_examples_linear_model_plot_bayesian_ridge_curvefit.py). وأخيرًا، بسبب القيود الداخلية للانحدار متعدد الحدود، يفشل كلا النموذجان عند الاستقراء.

Total running time of the script: (0 minutes 1.224 seconds)