ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

مثال على المربعات الصغرى العادية#

يوضح هذا المثال كيفية استخدام نموذج المربعات الصغرى العادية (OLS) المسمى LinearRegression في مكتبة ساي كيت ليرن (scikit-learn).

لهذا الغرض، نستخدم خاصية واحدة من مجموعة بيانات مرض السكري ونحاول التنبؤ بتطور مرض السكري باستخدام هذا النموذج الخطي. لذلك، نقوم بتحميل مجموعة بيانات مرض السكري وتقسيمها إلى مجموعات تدريب واختبار.

بعد ذلك، نقوم بضبط النموذج على مجموعة التدريب وتقييم أدائه على مجموعة الاختبار وأخيراً تصور النتائج على مجموعة الاختبار.

# المؤلفون: مطوري ساي كيت ليرن (scikit-learn)
# معرف الترخيص: BSD-3-Clause

تحميل البيانات والإعداد#

تحميل مجموعة بيانات مرض السكري. للتبسيط، سنحتفظ بخاصية واحدة فقط في البيانات. ثم نقوم بتقسيم البيانات والهدف إلى مجموعات تدريب واختبار.

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split

X, y = load_diabetes(return_X_y=True)
X = X[:, [2]]  # استخدام خاصية واحدة فقط
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, shuffle=False)

نموذج الانحدار الخطي#

نقوم بإنشاء نموذج انحدار خطي وضبطه على بيانات التدريب. لاحظ أنه بشكل افتراضي، يتم إضافة تقاطع إلى النموذج. يمكننا التحكم في هذا السلوك من خلال ضبط معامل fit_intercept.

from sklearn.linear_model import LinearRegression

pred = LinearRegression().fit(X_train, y_train)

تقييم النموذج#

نقوم بتقييم أداء النموذج على مجموعة الاختبار باستخدام متوسط الخطأ التربيعي ومعامل التحديد.

from sklearn.metrics import mean_squared_error, r2_score

y_pred = pred.predict(X_test)

print(f"متوسط الخطأ التربيعي: {mean_squared_error(y_test, y_pred):.2f}")
print(f"معامل التحديد: {r2_score(y_test, y_pred):.2f}")

متوسط الخطأ التربيعي: 2548.07
معامل التحديد: 0.47

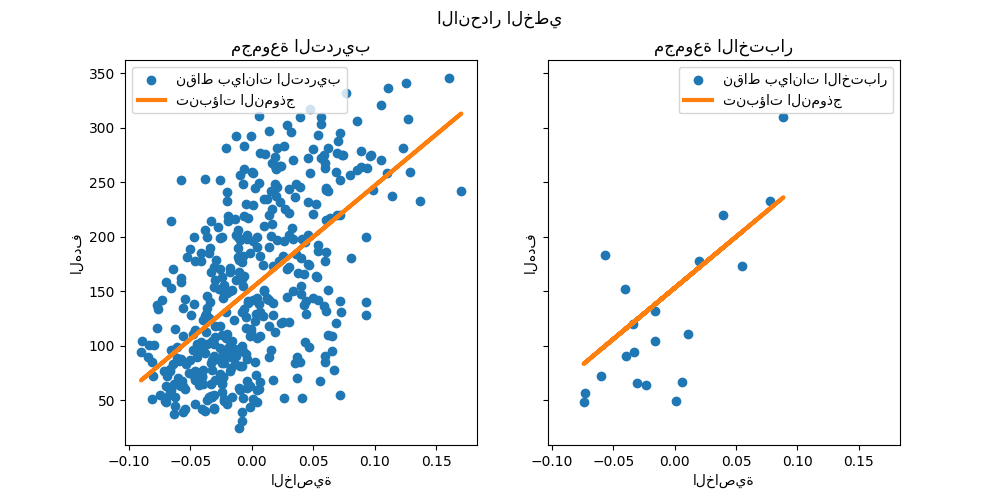
رسم النتائج#

أخيراً، نقوم بتصور النتائج على بيانات التدريب والاختبار.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)

ax[0].scatter(X_train, y_train, label="نقاط بيانات التدريب")
ax[0].plot(
    X_train,
    pred.predict(X_train),
    linewidth=3,
    color="tab:orange",
    label="تنبؤات النموذج",
)
ax[0].set(xlabel="الخاصية", ylabel="الهدف", title="مجموعة التدريب")
ax[0].legend()

ax[1].scatter(X_test, y_test, label="نقاط بيانات الاختبار")
ax[1].plot(X_test, y_pred, linewidth=3, color="tab:orange", label="تنبؤات النموذج")
ax[1].set(xlabel="الخاصية", ylabel="الهدف", title="مجموعة الاختبار")
ax[1].legend()

fig.suptitle("الانحدار الخطي")

plt.show()

الانحدار الخطي, مجموعة التدريب, مجموعة الاختبار

الخلاصة#

النموذج المدرب يتوافق مع المقدر الذي يقلل من متوسط الخطأ التربيعي بين القيم المتنبأ بها والقيم الحقيقية للهدف في بيانات التدريب. لذلك، نحصل على مقدر للمتوسط الشرطي للهدف معطى البيانات.

لاحظ أنه في الأبعاد الأعلى، قد يؤدي تقليل الخطأ التربيعي فقط إلى الإفراط في الملاءمة. لذلك، يتم استخدام تقنيات التنظيم بشكل شائع لمنع هذه المشكلة، مثل تلك المنفذة في Ridge أو Lasso.

Total running time of the script: (0 minutes 0.208 seconds)