انحدار كمي

يوضح هذا المثال كيف يمكن لانحدار كمي التنبؤ بالكميات الشرطية غير التافهة.

يوضح الشكل الأيسر الحالة عندما يكون توزيع الخطأ طبيعيًا، ولكن له تباين غير ثابت، أي مع تغاير التشتت.

يوضح الشكل الأيمن مثالًا لتوزيع خطأ غير متماثل، وهو توزيع باريتو.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

توليد مجموعة البيانات

لتوضيح سلوك انحدار كمي، سنقوم بإنشاء مجموعتي بيانات اصطناعية. ستتكون العمليات العشوائية التوليدية الحقيقية لكلا مجموعتي البيانات من نفس القيمة المتوقعة مع علاقة خطية مع ميزة واحدة x.

import numpy as np

rng = np.random.RandomState(42)
x = np.linspace(start=0, stop=10, num=100)
X = x[:, np.newaxis]
y_true_mean = 10 + 0.5 * x

سننشئ مشكلتين لاحقتين عن طريق تغيير توزيع الهدف y مع الحفاظ على نفس القيمة المتوقعة:

• في الحالة الأولى، تتم إضافة ضوضاء عادية غير متجانسة التشتت؛

• في الحالة الثانية، تتم إضافة ضوضاء باريتو غير متماثلة.

y_normal = y_true_mean + rng.normal(loc=0, scale=0.5 + 0.5 * x, size=x.shape[0])
a = 5
y_pareto = y_true_mean + 10 * (rng.pareto(a, size=x.shape[0]) - 1 / (a - 1))

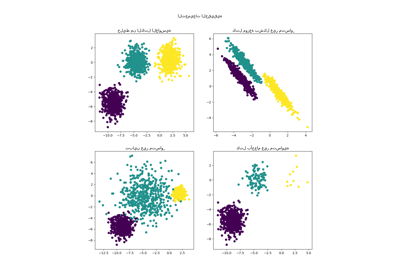
دعونا أولاً نقوم بتصور مجموعات البيانات بالإضافة إلى توزيع القيم المتبقية y - mean(y).

import matplotlib.pyplot as plt

_, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 11), sharex="row", sharey="row")

axs[0, 0].plot(x, y_true_mean, label="المتوسط الحقيقي")
axs[0, 0].scatter(x, y_normal, color="black", alpha=0.5, label="الملاحظات")
axs[1, 0].hist(y_true_mean - y_normal, edgecolor="black")


axs[0, 1].plot(x, y_true_mean, label="المتوسط الحقيقي")
axs[0, 1].scatter(x, y_pareto, color="black", alpha=0.5, label="الملاحظات")
axs[1, 1].hist(y_true_mean - y_pareto, edgecolor="black")

axs[0, 0].set_title("مجموعة بيانات مع أهداف موزعة بشكل عادي غير متجانسة التشتت")
axs[0, 1].set_title("مجموعة بيانات مع هدف موزع بشكل باريتو غير متماثل")
axs[1, 0].set_title(
    "توزيع القيم المتبقية لأهداف موزعة بشكل عادي غير متجانسة التشتت"
)
axs[1, 1].set_title("توزيع القيم المتبقية لهدف موزع بشكل باريتو غير متماثل")
axs[0, 0].legend()
axs[0, 1].legend()
axs[0, 0].set_ylabel("y")
axs[1, 0].set_ylabel("العدد")
axs[0, 1].set_xlabel("x")
axs[0, 0].set_xlabel("x")
axs[1, 0].set_xlabel("القيم المتبقية")
_ = axs[1, 1].set_xlabel("القيم المتبقية")

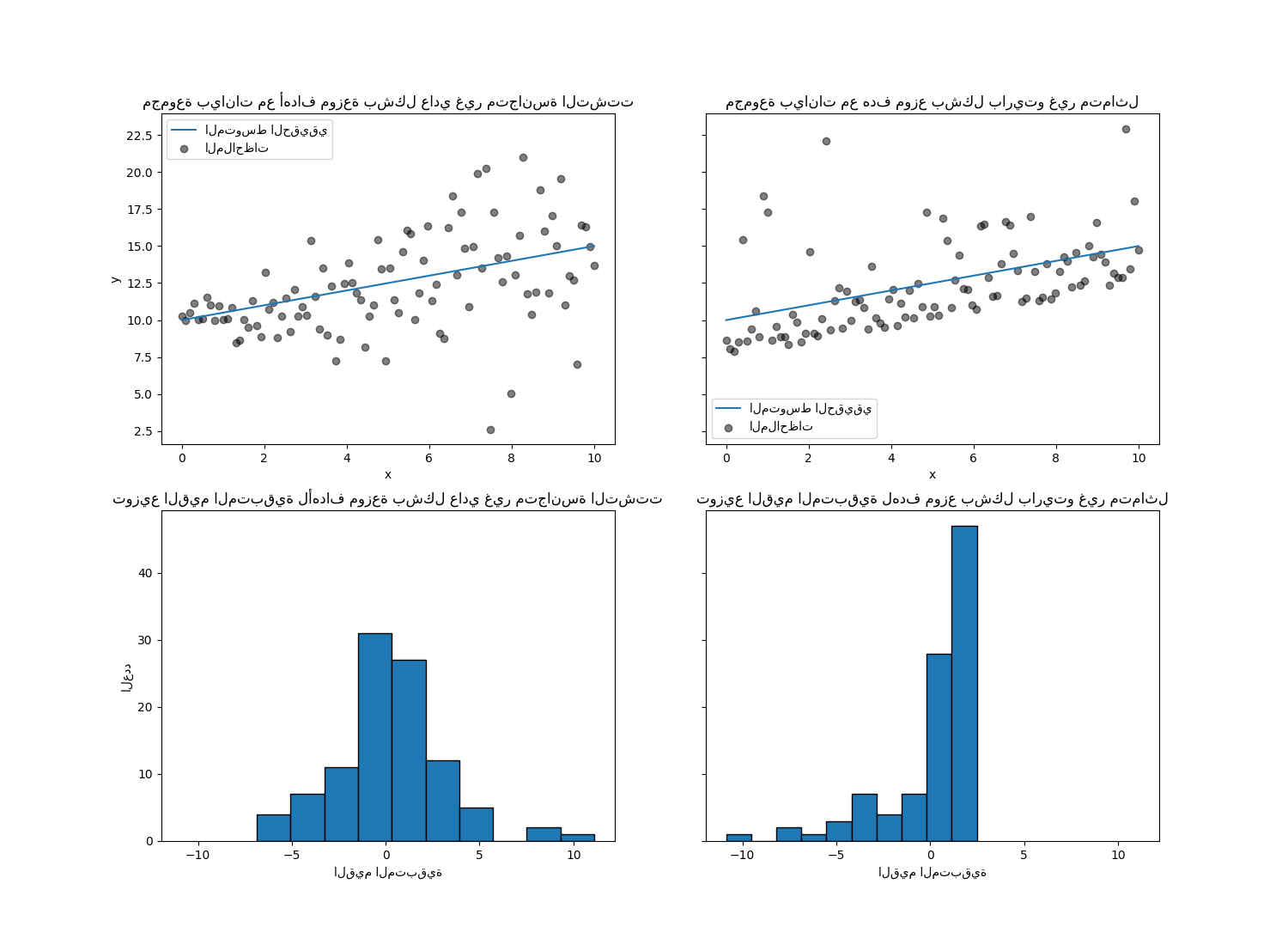
مع الهدف الموزع بشكل عادي غير متجانسة التشتت، نلاحظ أن تباين الضوضاء يزداد عندما تزداد قيمة الميزة x.

مع الهدف الموزع بشكل باريتو غير المتماثل، نلاحظ أن القيم المتبقية الإيجابية محدودة.

هذه الأنواع من الأهداف الصاخبة تجعل التقدير عبر LinearRegression أقل كفاءة، أي أننا نحتاج إلى المزيد من البيانات للحصول على نتائج مستقرة، بالإضافة إلى أن القيم المتطرفة الكبيرة يمكن أن يكون لها تأثير كبير على المعاملات المجهزة. (بعبارة أخرى: في بيئة ذات تباين ثابت، تتقارب مقدرات المربعات الصغرى العادية بشكل أسرع إلى المعاملات الحقيقية مع زيادة حجم العينة.)

في هذا الوضع غير المتماثل، يعطي الوسيط أو الكميات المختلفة رؤى إضافية. علاوة على ذلك، فإن تقدير الوسيط أكثر قوة بكثير للقيم المتطرفة والتوزيعات ذات الذيل الثقيل. لكن لاحظ أن الكميات المتطرفة يتم تقديرها بواسطة عدد قليل جدًا من نقاط البيانات. يتم تقدير الكمية 95% تقريبًا بواسطة أكبر 5% من القيم وبالتالي فهي أيضًا حساسة بعض الشيء للقيم المتطرفة.

في الجزء المتبقي من هذا البرنامج التعليمي، سنعرض كيفية استخدام QuantileRegressor في الممارسة العملية وإعطاء الحدس في خصائص النماذج المجهزة. أخيرًا، سنقارن كلاً من QuantileRegressor و LinearRegression.

ملاءمة QuantileRegressor

في هذا القسم، نريد تقدير الوسيط الشرطي بالإضافة إلى كمي منخفض وعالي تم تثبيتهما عند 5% و 95% على التوالي. وبالتالي، سنحصل على ثلاثة نماذج خطية، واحد لكل كمي.

سنستخدم الكميات عند 5% و 95% للعثور على القيم المتطرفة في عينة التدريب خارج الفاصل الزمني المركزي 90%.

from sklearn.linear_model import QuantileRegressor

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_normal).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_normal
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_normal
        )

الآن، يمكننا رسم النماذج الخطية الثلاثة والعينات المميزة التي تقع ضمن الفاصل الزمني المركزي 90% من العينات التي تقع خارج هذا الفاصل الزمني.

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="المتوسط الحقيقي")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"الكمية: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_normal[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="خارج الفاصل الزمني",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_normal[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="داخل الفاصل الزمني",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("الكميات للهدف الموزع بشكل عادي غير متجانسة التشتت")

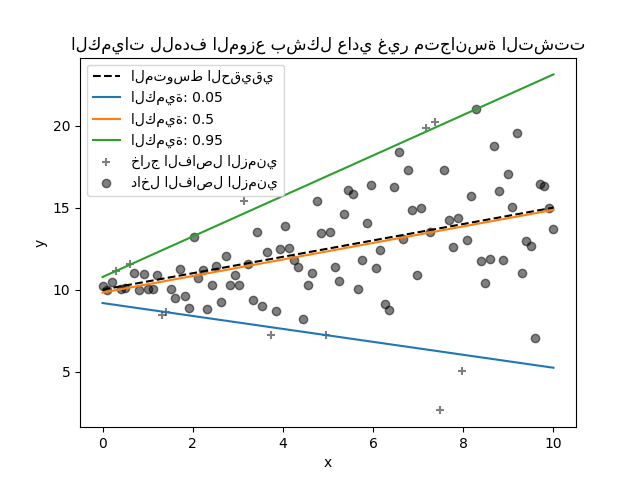
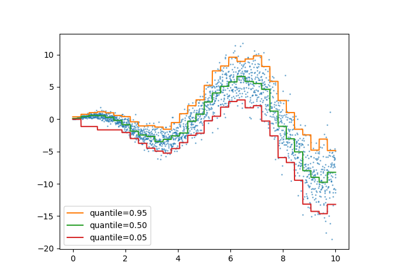
نظرًا لأن الضوضاء لا تزال موزعة بشكل طبيعي، وخاصة متماثلة، فإن المتوسط الشرطي الحقيقي والوسيط الشرطي الحقيقي يتطابقان. في الواقع، نرى أن الوسيط المقدر يكاد يصطدم بالمتوسط الحقيقي. نلاحظ تأثير وجود تباين ضوضاء متزايد على الكميات 5% و 95%: منحدرات هذه الكميات مختلفة جدًا والفاصل الزمني بينها يصبح أوسع مع زيادة x.

للحصول على حدس إضافي بشأن معنى مقدرات الكميات 5% و 95%، يمكن للمرء حساب عدد العينات أعلى وأسفل الكميات المتوقعة (ممثلة بصليب على الرسم البياني أعلاه)، مع الأخذ في الاعتبار أن لدينا ما مجموعه 100 عينة.

يمكننا تكرار نفس التجربة باستخدام الهدف الموزع بشكل باريتو غير المتماثل.

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_pareto).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_pareto
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_pareto
        )

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="المتوسط الحقيقي")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"الكمية: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_pareto[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="خارج الفاصل الزمني",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_pareto[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="داخل الفاصل الزمني",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("الكميات للهدف الموزع بشكل باريتو غير المتماثل")

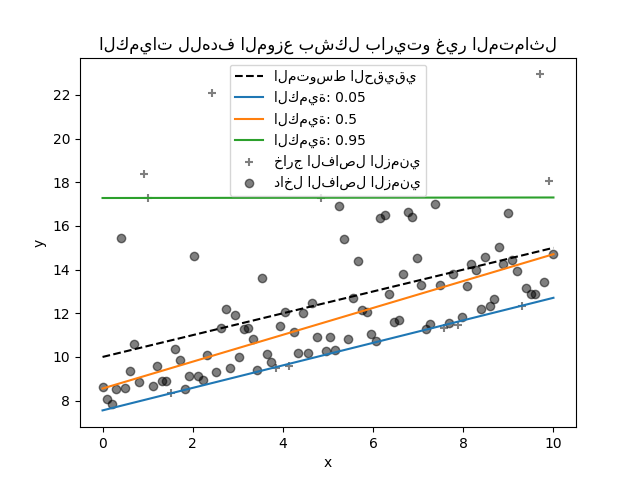
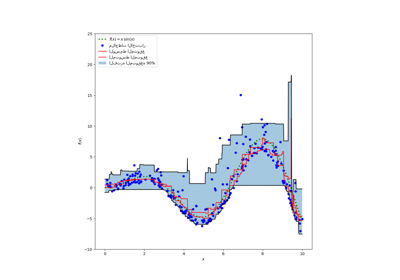
نظرًا لعدم تناسق توزيع الضوضاء، نلاحظ أن المتوسط الحقيقي والوسيط الشرطي المقدر مختلفان. نلاحظ أيضًا أن كل نموذج كمي له معلمات مختلفة لملاءمة الكمية المطلوبة بشكل أفضل. لاحظ أنه من الناحية المثالية، ستكون جميع الكميات متوازية في هذه الحالة، وهو ما سيصبح أكثر وضوحًا مع المزيد من نقاط البيانات أو الكميات الأقل تطرفًا، على سبيل المثال 10% و 90%.

مقارنة QuantileRegressor و LinearRegression

في هذا القسم، سنتوقف عند الاختلاف فيما يتعلق بالخطأ الذي يقوم QuantileRegressor و LinearRegression بتقليله.

في الواقع، LinearRegression هو نهج المربعات الصغرى الذي يقلل من متوسط ​​مربع الخطأ (MSE) بين أهداف التدريب والتنبؤ. في المقابل، QuantileRegressor مع quantile=0.5 يقلل من متوسط ​​الخطأ المطلق (MAE) بدلاً من ذلك.

دعونا أولاً نحسب أخطاء التدريب لمثل هذه النماذج من حيث متوسط ​​مربع الخطأ ومتوسط ​​الخطأ المطلق. سنستخدم الهدف الموزع بشكل باريتو غير المتماثل لجعله أكثر إثارة للاهتمام لأن المتوسط ​​والوسيط ليسا متساويين.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

linear_regression = LinearRegression()
quantile_regression = QuantileRegressor(quantile=0.5, alpha=0)

y_pred_lr = linear_regression.fit(X, y_pareto).predict(X)
y_pred_qr = quantile_regression.fit(X, y_pareto).predict(X)

print(
    f"""خطأ التدريب (الأداء داخل العينة)
    {linear_regression.__class__.__name__}:
    MAE = {mean_absolute_error(y_pareto, y_pred_lr):.3f}
    MSE = {mean_squared_error(y_pareto, y_pred_lr):.3f}
    {quantile_regression.__class__.__name__}:
    MAE = {mean_absolute_error(y_pareto, y_pred_qr):.3f}
    MSE = {mean_squared_error(y_pareto, y_pred_qr):.3f}
    """
)

خطأ التدريب (الأداء داخل العينة)
    LinearRegression:
    MAE = 1.805
    MSE = 6.486
    QuantileRegressor:
    MAE = 1.670
    MSE = 7.025

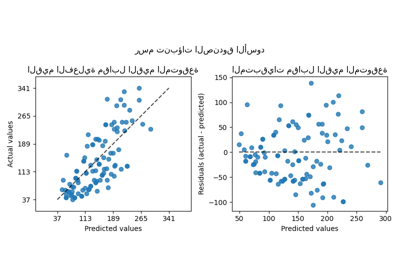
في مجموعة التدريب، نرى أن MAE أقل بالنسبة لـ QuantileRegressor من LinearRegression. على عكس ذلك، فإن MSE أقل بالنسبة لـ LinearRegression من QuantileRegressor. تؤكد هذه النتائج أن MAE هي الخسارة التي تم تقليلها بواسطة QuantileRegressor بينما MSE هي الخسارة التي تم تقليلها بواسطة LinearRegression.

يمكننا إجراء تقييم مشابه من خلال النظر إلى خطأ الاختبار الذي تم الحصول عليه عن طريق التحقق المتقاطع.

from sklearn.model_selection import cross_validate

cv_results_lr = cross_validate(
    linear_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
cv_results_qr = cross_validate(
    quantile_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
print(
    f"""خطأ الاختبار (الأداء المتحقق متقاطعًا)
    {linear_regression.__class__.__name__}:
    MAE = {-cv_results_lr["test_neg_mean_absolute_error"].mean():.3f}
    MSE = {-cv_results_lr["test_neg_mean_squared_error"].mean():.3f}
    {quantile_regression.__class__.__name__}:
    MAE = {-cv_results_qr["test_neg_mean_absolute_error"].mean():.3f}
    MSE = {-cv_results_qr["test_neg_mean_squared_error"].mean():.3f}
    """
)

خطأ الاختبار (الأداء المتحقق متقاطعًا)
    LinearRegression:
    MAE = 1.732
    MSE = 6.690
    QuantileRegressor:
    MAE = 1.679
    MSE = 7.129

نصل إلى استنتاجات مماثلة في التقييم خارج العينة.

Related examples

فترات التنبؤ لانحدار التعزيز المتدرج

فترات التنبؤ لانحدار التعزيز المتدرج

رسم تنبؤات الصندوق الأسود

رسم تنبؤات الصندوق الأسود

أبرز الميزات الجديدة في إصدار scikit-learn 1.1

أبرز الميزات الجديدة في إصدار scikit-learn 1.1

توضيح افتراضات خوارزمية كاي-مينز

توضيح افتراضات خوارزمية كاي-مينز