ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
حدود القرار للانحدار متعدد الحدود والانحدار اللوجستي من النوع واحد مقابل البقية#
يقارن هذا المثال حدود القرار للانحدار متعدد الحدود والانحدار اللوجستي من النوع واحد مقابل البقية على مجموعة بيانات ثنائية الأبعاد بثلاث فئات.
نقوم بمقارنة حدود القرار لكلتا الطريقتين والتي تعادل استدعاء طريقة predict. بالإضافة إلى ذلك، نقوم برسم المستويات الفاصلة التي تقابل
الخط عندما يكون تقدير الاحتمال لفئة معينة 0.5.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
توليد مجموعة البيانات#
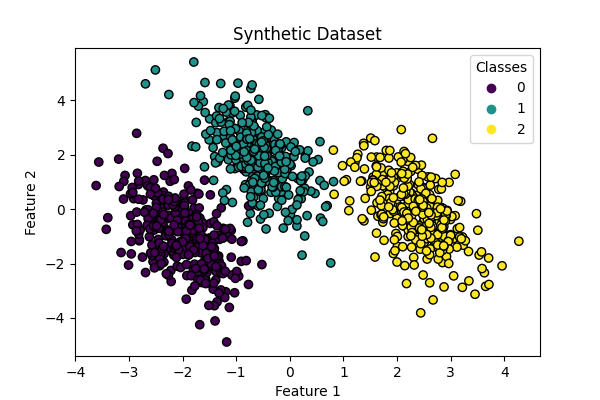
نقوم بتوليد مجموعة بيانات اصطناعية باستخدام الدالة make_blobs.
تتكون مجموعة البيانات من 1,000 عينة من ثلاث فئات مختلفة،
تتركز حول النقاط [-5, 0], [0, 1.5], و [5, -1]. بعد التوليد، نقوم بتطبيق تحويل خطي
لإدخال بعض الارتباط بين الميزات وجعل المشكلة
أكثر صعوبة. ينتج عن ذلك مجموعة بيانات ثنائية الأبعاد بثلاث فئات متداخلة،
مناسبة لإظهار الاختلافات بين الانحدار متعدد الحدود والانحدار اللوجستي من النوع واحد مقابل البقية.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
centers = [[-5, 0], [0, 1.5], [5, -1]]
X, y = make_blobs(n_samples=1_000, centers=centers, random_state=40)
transformation = [[0.4, 0.2], [-0.4, 1.2]]
X = np.dot(X, transformation)
fig, ax = plt.subplots(figsize=(6, 4))
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="black")
ax.set(title="Synthetic Dataset", xlabel="Feature 1", ylabel="Feature 2")
_ = ax.legend(*scatter.legend_elements(), title="Classes")
تدريب المصنف#
نقوم بتدريب مصنفين مختلفين للانحدار اللوجستي: متعدد الحدود والنوع واحد مقابل البقية. يتعامل المصنف متعدد الحدود مع جميع الفئات في نفس الوقت، بينما يقوم النوع واحد مقابل البقية بتدريب مصنف ثنائي لكل فئة مقابل جميع الفئات الأخرى.
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier
logistic_regression_multinomial = LogisticRegression().fit(X, y)
logistic_regression_ovr = OneVsRestClassifier(LogisticRegression()).fit(X, y)
accuracy_multinomial = logistic_regression_multinomial.score(X, y)
accuracy_ovr = logistic_regression_ovr.score(X, y)
تصور حدود القرار#
دعنا نصور حدود القرار لكل من النموذجين والتي يوفرها
طريقة predict للمصنفين.
from sklearn.inspection import DecisionBoundaryDisplay
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)
for model, title, ax in [
(
logistic_regression_multinomial,
f"Multinomial Logistic Regression\n(Accuracy: {accuracy_multinomial:.3f})",
ax1,
),
(
logistic_regression_ovr,
f"One-vs-Rest Logistic Regression\n(Accuracy: {accuracy_ovr:.3f})",
ax2,
),
]:
DecisionBoundaryDisplay.from_estimator(
model,
X,
ax=ax,
response_method="predict",
alpha=0.8,
)
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
legend = ax.legend(*scatter.legend_elements(), title="Classes")
ax.add_artist(legend)
ax.set_title(title)
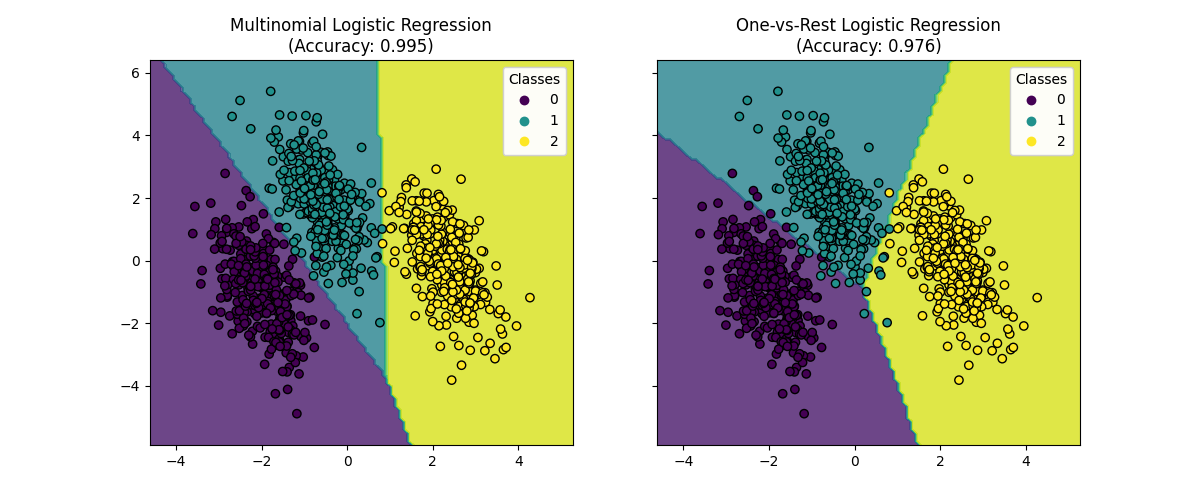
نرى أن حدود القرار مختلفة. ينبع هذا الاختلاف من نهجهم:
الانحدار اللوجستي متعدد الحدود يأخذ في الاعتبار جميع الفئات في نفس الوقت أثناء التحسين.
الانحدار اللوجستي من النوع واحد مقابل البقية يقوم بتدريب كل فئة بشكل مستقل مقابل جميع الفئات الأخرى.
يمكن لهذه الاستراتيجيات المتميزة أن تؤدي إلى حدود قرار مختلفة، خاصة في المشاكل متعددة الفئات المعقدة.
تصور المستويات الفاصلة#
نقوم أيضا بتصور المستويات الفاصلة التي تقابل الخط عندما يكون تقدير الاحتمال لفئة معينة 0.5.
def plot_hyperplanes(classifier, X, ax):
xmin, xmax = X[:, 0].min(), X[:, 0].max()
ymin, ymax = X[:, 1].min(), X[:, 1].max()
ax.set(xlim=(xmin, xmax), ylim=(ymin, ymax))
if isinstance(classifier, OneVsRestClassifier):
coef = np.concatenate([est.coef_ for est in classifier.estimators_])
intercept = np.concatenate([est.intercept_ for est in classifier.estimators_])
else:
coef = classifier.coef_
intercept = classifier.intercept_
for i in range(coef.shape[0]):
w = coef[i]
a = -w[0] / w[1]
xx = np.linspace(xmin, xmax)
yy = a * xx - (intercept[i]) / w[1]
ax.plot(xx, yy, "--", linewidth=3, label=f"Class {i}")
return ax.get_legend_handles_labels()
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)
for model, title, ax in [
(
logistic_regression_multinomial,
"Multinomial Logistic Regression Hyperplanes",
ax1,
),
(logistic_regression_ovr, "One-vs-Rest Logistic Regression Hyperplanes", ax2),
]:
hyperplane_handles, hyperplane_labels = plot_hyperplanes(model, X, ax)
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
scatter_handles, scatter_labels = scatter.legend_elements()
all_handles = hyperplane_handles + scatter_handles
all_labels = hyperplane_labels + scatter_labels
ax.legend(all_handles, all_labels, title="Classes")
ax.set_title(title)
plt.show()
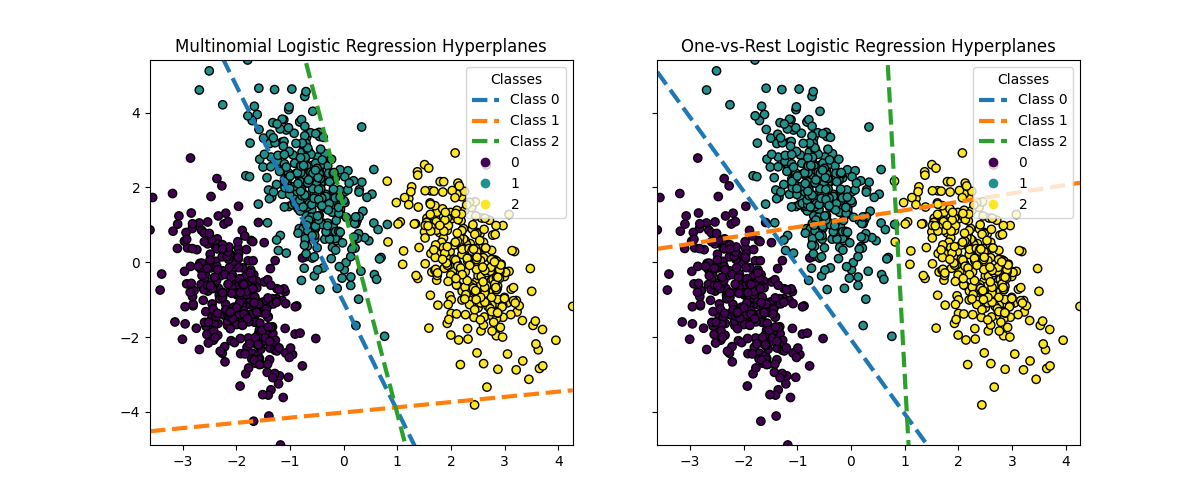
بينما المستويات الفاصلة للفئتين 0 و 2 متشابهة إلى حد ما بين الطريقتين، نلاحظ أن المستوى الفاصل للفئة 1 مختلف بشكل ملحوظ. ينبع هذا الاختلاف من النهج الأساسي للانحدار اللوجستي من النوع واحد مقابل البقية والانحدار اللوجستي متعدد الحدود:
بالنسبة للانحدار اللوجستي من النوع واحد مقابل البقية:
يتم تحديد كل مستوى فاصل بشكل مستقل من خلال اعتبار فئة واحدة مقابل جميع الفئات الأخرى.
بالنسبة للفئة 1، يمثل المستوى الفاصل حد القرار الذي يفصل بشكل أفضل الفئة 1 عن الفئتين 0 و 2 مجتمعتين.
يمكن لهذا النهج الثنائي أن يؤدي إلى حدود قرار أبسط ولكن قد لا يلتقط العلاقات المعقدة بين جميع الفئات في نفس الوقت.
لا يوجد تفسير ممكن للاحتمالات الشرطية للفئات.
بالنسبة للانحدار اللوجستي متعدد الحدود:
يتم تحديد جميع المستويات الفاصلة في نفس الوقت، مع مراعاة العلاقات بين جميع الفئات في نفس الوقت.
الخسارة التي يتم تقليلها بواسطة النموذج هي قاعدة تسجيل صحيحة، مما يعني أن النموذج يتم تحسينه لتقدير الاحتمالات الشرطية للفئات والتي تكون بالتالي ذات معنى.
يمثل كل مستوى فاصل حد القرار حيث يصبح احتمال فئة واحدة أعلى من الفئات الأخرى، بناءً على توزيع الاحتمالات الكلي.
يمكن لهذا النهج أن يلتقط العلاقات الأكثر دقة بين الفئات، مما يؤدي إلى تصنيف أكثر دقة في المشاكل متعددة الفئات.
يبرز الاختلاف في المستويات الفاصلة، خاصة للفئة 1، كيف يمكن لهذه الطرق أن تنتج حدود قرار مختلفة على الرغم من الدقة الكلية المتشابهة.
في الممارسة العملية، يوصى باستخدام الانحدار اللوجستي متعدد الحدود لأنه يقلل من دالة خسارة جيدة الصياغة، مما يؤدي إلى احتمالات أكثر توازناً للفئات وبالتالي نتائج أكثر قابلية للتفسير. عندما يتعلق الأمر بحدود القرار، يجب صياغة دالة فائدة لتحويل احتمالات الفئات إلى كمية ذات معنى للمشكلة المطروحة. يسمح النوع واحد مقابل البقية بحدود قرار مختلفة ولكن لا يسمح بالتحكم الدقيق في المقايضة بين الفئات كما تفعل دالة الفائدة.
Total running time of the script: (0 minutes 0.814 seconds)
Related examples
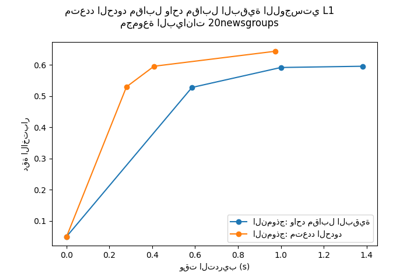
الانحدار اللوجستي المتناثر متعدد الفئات على 20newgroups
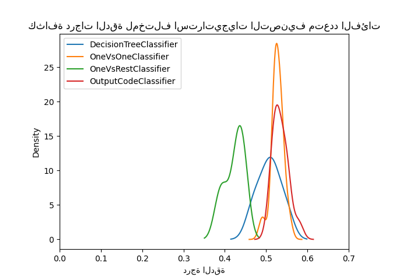
نظرة عامة على الميتا-مقدّرات التدريب متعدد التصنيفات