ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
نموذج لاصو: اختيار النموذج باستخدام معايير AIC-BIC والتحقق المتقاطع#
يركز هذا المثال على اختيار النموذج لنموذج لاصو، وهي نماذج خطية مع عقوبة L1 لمشاكل الانحدار.
في الواقع، يمكن استخدام عدة استراتيجيات لاختيار قيمة معامل التنظيم: من خلال التحقق المتقاطع أو باستخدام معيار المعلومات، مثل AIC أو BIC.
فيما يلي، سنناقش بالتفصيل الاستراتيجيات المختلفة.
# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause
مجموعة البيانات#
في هذا المثال، سنستخدم مجموعة بيانات مرض السكري.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
X.head()
بالإضافة إلى ذلك، سنضيف بعض الميزات العشوائية إلى البيانات الأصلية لتوضيح بشكل أفضل عملية اختيار الميزات التي يقوم بها نموذج لاصو.
import numpy as np
import pandas as pd
rng = np.random.RandomState(42)
n_random_features = 14
X_random = pd.DataFrame(
rng.randn(X.shape[0], n_random_features),
columns=[f"random_{i:02d}" for i in range(n_random_features)],
)
X = pd.concat([X, X_random], axis=1)
# عرض مجموعة فرعية فقط من الأعمدة
X[X.columns[::3]].head()
اختيار نموذج لاصو باستخدام معيار المعلومات#
LassoLarsIC يوفر نموذج لاصو يستخدم معيار
معلومات أكايكي (AIC) أو معيار معلومات بايز (BIC) لاختيار القيمة المثلى لمعامل
التنظيم alpha.
قبل ملاءمة النموذج، سنقوم بتوحيد البيانات باستخدام
StandardScaler. بالإضافة إلى ذلك، سنقوم
بقياس الوقت لملاءمة وضبط معامل alpha لكي نقارن مع استراتيجية التحقق المتقاطع.
سنقوم أولاً بملاءمة نموذج لاصو باستخدام معيار AIC.
import time
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
start_time = time.time()
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
fit_time = time.time() - start_time
سنخزن معيار AIC لكل قيمة من قيم alpha المستخدمة خلال fit.
results = pd.DataFrame(
{
"alphas": lasso_lars_ic[-1].alphas_,
"AIC criterion": lasso_lars_ic[-1].criterion_,
}
).set_index("alphas")
alpha_aic = lasso_lars_ic[-1].alpha_
الآن، سنقوم بنفس التحليل باستخدام معيار BIC.
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
results["BIC criterion"] = lasso_lars_ic[-1].criterion_
alpha_bic = lasso_lars_ic[-1].alpha_
يمكننا التحقق من قيمة alpha التي تؤدي إلى الحد الأدنى من AIC وBIC.
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results.style.apply(highlight_min)
أخيراً، يمكننا رسم قيم AIC وBIC لمختلف قيم alpha. الخطوط العمودية في الرسم البياني تقابل قيمة alpha المختارة لكل معيار. قيمة alpha المختارة تقابل الحد الأدنى من معيار AIC أو BIC.
ax = results.plot()
ax.vlines(
alpha_aic,
results["AIC criterion"].min(),
results["AIC criterion"].max(),
label="alpha: AIC estimate",
linestyles="--",
color="tab:blue",
)
ax.vlines(
alpha_bic,
results["BIC criterion"].min(),
results["BIC criterion"].max(),
label="alpha: BIC estimate",
linestyle="--",
color="tab:orange",
)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel("criterion")
ax.set_xscale("log")
ax.legend()
_ = ax.set_title(
f"Information-criterion for model selection (training time {fit_time:.2f}s)"
)
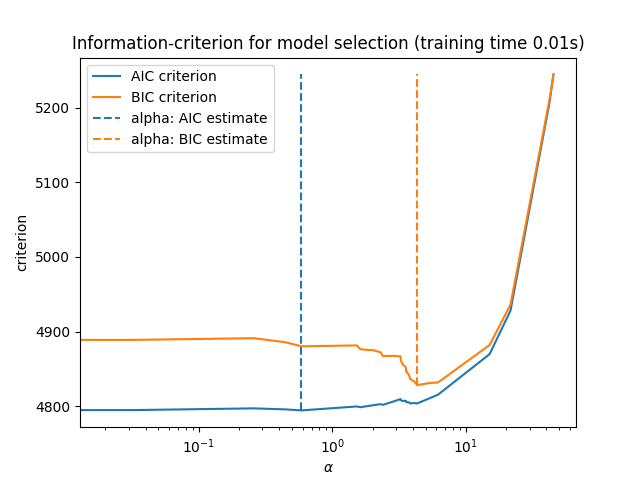
اختيار النموذج باستخدام معيار المعلومات سريع للغاية. يعتمد على
حساب المعيار على مجموعة العينات المقدمة إلى fit. كلا المعيارين
يقدران خطأ تعميم النموذج بناءً على خطأ مجموعة التدريب ويعاقبان هذا الخطأ
المتفائل بشكل مفرط. ومع ذلك، تعتمد هذه العقوبة على تقدير صحيح لدرجات الحرية
وتقلب الضوضاء. يتم اشتقاق كلاهما للعينات الكبيرة (النتائج التقاربية) ويفترض
أن النموذج صحيح، أي أن البيانات يتم توليدها بالفعل بواسطة هذا النموذج.
تميل هذه النماذج أيضًا إلى التعطل عندما تكون المشكلة سيئة التكييف (أكثر من الميزات من العينات). عندها يكون من الضروري توفير تقدير لتقلب الضوضاء.
اختيار نموذج لاصو باستخدام التحقق المتقاطع#
يمكن تنفيذ نموذج لاصو باستخدام محسنات مختلفة: الانحدار المنسق والانحدار بزاوية أقل. تختلف هذه المحسنات فيما يتعلق بسرعة التنفيذ ومصادر الأخطاء العددية.
في سكايت-ليرن، هناك محسنان مختلفان متاحان مع التحقق المتقاطع المدمج:
LassoCV و:class:~sklearn.linear_model.LassoLarsCV
اللذان يحلان المشكلة باستخدام الانحدار المنسق والانحدار بزاوية أقل على
التوالي.
في بقية هذا القسم، سنقدم كلا النهجين. بالنسبة لكلا الخوارزميتين، سنستخدم استراتيجية التحقق المتقاطع 20-fold.
نموذج لاصو باستخدام الانحدار المنسق#
دعنا نبدأ بضبط المعامل باستخدام
LassoCV.
from sklearn.linear_model import LassoCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
import matplotlib.pyplot as plt
ymin, ymax = 2300, 3800
lasso = model[-1]
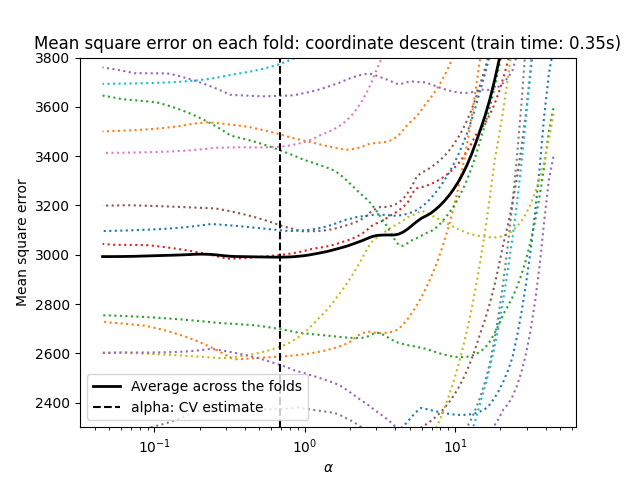
plt.semilogx(lasso.alphas_, lasso.mse_path_, linestyle=":")
plt.plot(
lasso.alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha: CV estimate")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(
f"Mean square error on each fold: coordinate descent (train time: {fit_time:.2f}s)"
)
نموذج لاصو باستخدام الانحدار بزاوية أقل#
دعنا نبدأ بضبط المعامل باستخدام
LassoLarsCV.
from sklearn.linear_model import LassoLarsCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoLarsCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
lasso = model[-1]
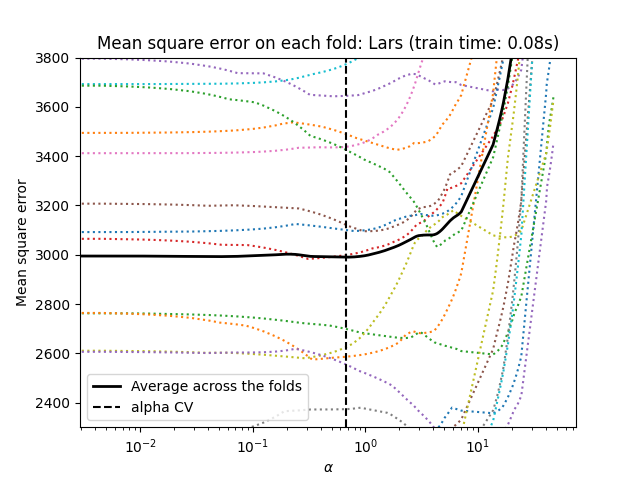
plt.semilogx(lasso.cv_alphas_, lasso.mse_path_, ":")
plt.semilogx(
lasso.cv_alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha CV")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(f"Mean square error on each fold: Lars (train time: {fit_time:.2f}s)")
ملخص نهج التحقق المتقاطع#
كلا الخوارزميتين تعطيان نتائج متشابهة تقريبًا.
يحسب Lars مسار الحل فقط لكل انحناء في المسار. ونتيجة لذلك، فهو فعال للغاية عندما يكون هناك عدد قليل من الانحناءات، وهو الحال إذا كان هناك عدد قليل من الميزات أو العينات. كما أنه قادر على حساب المسار الكامل دون ضبط أي معامل. على العكس، يحسب الانحدار المنسق نقاط المسار على شبكة محددة مسبقًا (هنا نستخدم الافتراضية). وبالتالي فهو أكثر كفاءة إذا كان عدد نقاط الشبكة أصغر من عدد الانحناءات في المسار. يمكن أن تكون هذه الاستراتيجية مثيرة للاهتمام إذا كان عدد الميزات كبيرًا جدًا وكان هناك ما يكفي من العينات ليتم اختيارها في كل طية من طيات التحقق المتقاطع. من حيث الأخطاء العددية، بالنسبة للمتغيرات المترابطة بشدة، سيتراكم Lars المزيد من الأخطاء، بينما سيقوم خوارزمية الانحدار المنسق باختيار المسار فقط على شبكة.
لاحظ كيف تختلف القيمة المثلى لـ alpha لكل طية. يوضح هذا لماذا يعد التحقق المتقاطع المضمن استراتيجية جيدة عند محاولة تقييم أداء طريقة يتم اختيار معامل لها بواسطة التحقق المتقاطع: قد لا يكون هذا الاختيار للمعامل الأمثل للتقييم النهائي على مجموعة اختبار غير مرئية فقط.
الخلاصة#
في هذا البرنامج التعليمي، قدمنا نهجين لاختيار أفضل معامل
alpha: استراتيجية واحدة تجد القيمة المثلى لـ alpha
باستخدام مجموعة التدريب فقط وبعض معايير المعلومات، واستراتيجية أخرى
تعتمد على التحقق المتقاطع.
في هذا المثال، يعمل كلا النهجين بشكل مشابه. اختيار المعامل داخل العينة يظهر حتى فعاليته من حيث الأداء الحسابي. ومع ذلك، يمكن استخدامه فقط عندما يكون عدد العينات كبيرًا بما فيه الكفاية مقارنةً بعدد الميزات.
لهذا السبب، يعد ضبط المعامل باستخدام التحقق المتقاطع استراتيجية آمنة: تعمل في إعدادات مختلفة.
Total running time of the script: (0 minutes 1.165 seconds)
Related examples
التحقق المتقاطع على تمرين مجموعة بيانات مرض السكري