ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تصور سلوك التحقق المتقاطع في سكايلرن#

يعد اختيار كائن التحقق المتقاطع المناسب جزءًا حاسمًا من ملاءمة النموذج بشكل صحيح. هناك العديد من الطرق لتقسيم البيانات إلى مجموعات تدريب واختبار لتجنب الإفراط في تناسب النموذج، وتوحيد عدد المجموعات في مجموعات الاختبار، وما إلى ذلك.

يوضح هذا المثال سلوك العديد من كائنات سكايلرن الشائعة للمقارنة.

# المؤلفون: مطوري سكايلرن
# معرف SPDX-License: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Patch

from sklearn.model_selection import (
    GroupKFold,
    GroupShuffleSplit,
    KFold,
    ShuffleSplit,
    StratifiedGroupKFold,
    StratifiedKFold,
    StratifiedShuffleSplit,
    TimeSeriesSplit,
)

rng = np.random.RandomState(1338)
cmap_data = plt.cm.Paired
cmap_cv = plt.cm.coolwarm
n_splits = 4

تصور بياناتنا#

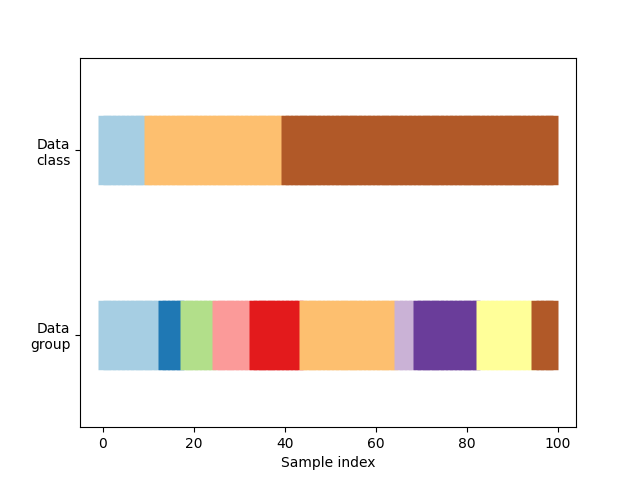
أولاً، يجب أن نفهم بنية بياناتنا. يحتوي على 100 نقطة بيانات إدخال تم إنشاؤها عشوائيًا، و3 فئات مقسمة بشكل غير متساوٍ عبر نقاط البيانات، و10 "مجموعات" مقسمة بالتساوي عبر نقاط البيانات.

كما سنرى، فإن بعض كائنات التحقق المتقاطع تقوم بأشياء محددة مع البيانات المسمى، والبعض الآخر يتصرف بشكل مختلف مع البيانات المجمعة، والبعض الآخر لا تستخدم هذه المعلومات.

للبدء، سنقوم بتصور بياناتنا.

# توليد بيانات الفئة/المجموعة
n_points = 100
X = rng.randn(100, 10)

percentiles_classes = [0.1, 0.3, 0.6]
y = np.hstack([[ii] * int(100 * perc) for ii, perc in enumerate(percentiles_classes)])

# توليد مجموعات غير متساوية
group_prior = rng.dirichlet([2] * 10)
groups = np.repeat(np.arange(10), rng.multinomial(100, group_prior))


def visualize_groups(classes, groups, name):
    # تصور مجموعات مجموعة البيانات
    fig, ax = plt.subplots()
    ax.scatter(
        range(len(groups)),
        [0.5] * len(groups),
        c=groups,
        marker="_",
        lw=50,
        cmap=cmap_data,
    )
    ax.scatter(
        range(len(groups)),
        [3.5] * len(groups),
        c=classes,
        marker="_",
        lw=50,
        cmap=cmap_data,
    )
    ax.set(
        ylim=[-1, 5],
        yticks=[0.5, 3.5],
        yticklabels=["Data\ngroup", "Data\nclass"],
        xlabel="Sample index",
    )


visualize_groups(y, groups, "no groups")

تحديد وظيفة لتصور سلوك التحقق المتقاطع#

سنقوم بتعريف وظيفة تسمح لنا بتصور سلوك كل كائن تحقق متقاطع. سنقوم بأداء 4 انقسامات للبيانات. في كل تقسيم، سنقوم بتصور المؤشرات المختارة لمجموعة التدريب (باللون الأزرق) ومجموعة الاختبار (باللون الأحمر).

def plot_cv_indices(cv, X, y, group, ax, n_splits, lw=10):
    """إنشاء رسم بياني عينة لمؤشرات كائن التحقق المتقاطع."""
    use_groups = "Group" in type(cv).__name__
    groups = group if use_groups else None
    # توليد التصورات التدريب/الاختبار لكل تقسيم CV
    for ii, (tr, tt) in enumerate(cv.split(X=X, y=y, groups=groups)):
        # ملء المؤشرات بمجموعات التدريب/الاختبار
        indices = np.array([np.nan] * len(X))
        indices[tt] = 1
        indices[tr] = 0

        # تصور النتائج
        ax.scatter(
            range(len(indices)),
            [ii + 0.5] * len(indices),
            c=indices,
            marker="_",
            lw=lw,
            cmap=cmap_cv,
            vmin=-0.2,
            vmax=1.2,
        )

    # رسم فئات البيانات والمجموعات في النهاية
    ax.scatter(
        range(len(X)), [ii + 1.5] * len(X), c=y, marker="_", lw=lw, cmap=cmap_data
    )

    ax.scatter(
        range(len(X)), [ii + 2.5] * len(X), c=group, marker="_", lw=lw, cmap=cmap_data
    )

    # التنسيق
    yticklabels = list(range(n_splits)) + ["class", "group"]
    ax.set(
        yticks=np.arange(n_splits + 2) + 0.5,
        yticklabels=yticklabels,
        xlabel="Sample index",
        ylabel="CV iteration",
        ylim=[n_splits + 2.2, -0.2],
        xlim=[0, 100],
    )
    ax.set_title("{}".format(type(cv).__name__), fontsize=15)
    return ax

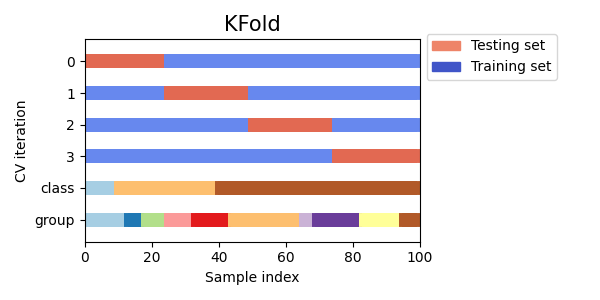
دعونا نرى كيف يبدو الأمر بالنسبة لكائن KFold كائن التحقق المتقاطع:

fig, ax = plt.subplots()
cv = KFold(n_splits)
plot_cv_indices(cv, X, y, groups, ax, n_splits)

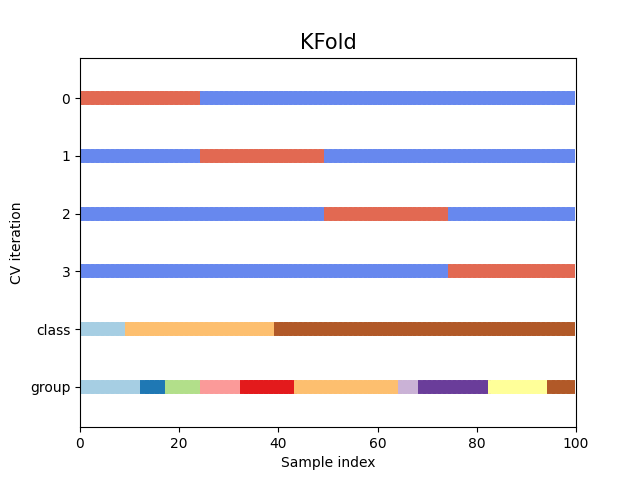
<Axes: title={'center': 'KFold'}, xlabel='Sample index', ylabel='CV iteration'>

كما ترى، بشكل افتراضي، لا يأخذ منشئ التقسيم المتقاطع KFold في الاعتبار فئة نقطة البيانات أو المجموعة. يمكننا تغيير هذا باستخدام أي مما يلي:

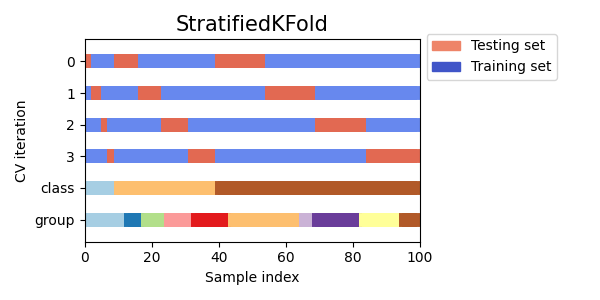
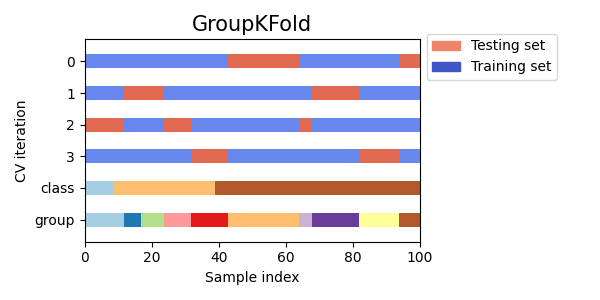
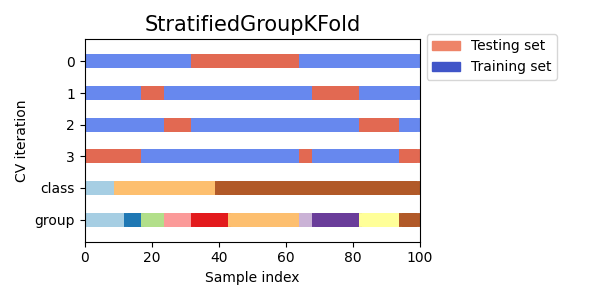
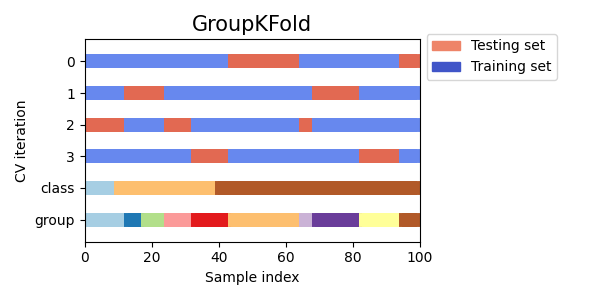
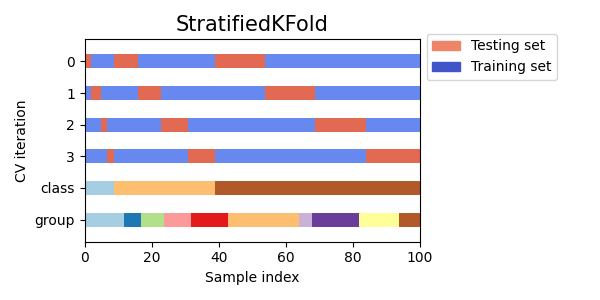
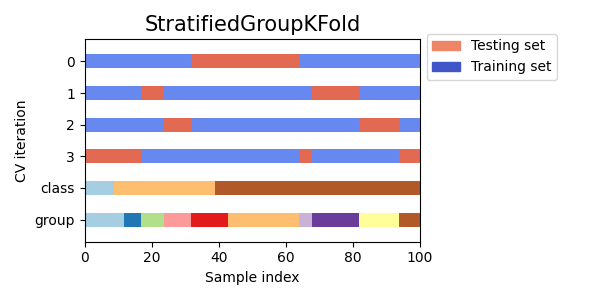
StratifiedKFold للحفاظ على نسبة العينات لكل فئة.
GroupKFold لضمان عدم ظهور نفس المجموعة في طيتين مختلفتين.
StratifiedGroupKFold للحفاظ على قيد GroupKFold مع محاولة إرجاع الطيات المفهرسة.

cvs = [StratifiedKFold, GroupKFold, StratifiedGroupKFold]

for cv in cvs:
    fig, ax = plt.subplots(figsize=(6, 3))
    plot_cv_indices(cv(n_splits), X, y, groups, ax, n_splits)
    ax.legend(
        [Patch(color=cmap_cv(0.8)), Patch(color=cmap_cv(0.02))],
        ["Testing set", "Training set"],
        loc=(1.02, 0.8),
    )
    # ضبط الأسطورة
    plt.tight_layout()
    fig.subplots_adjust(right=0.7)

بعد ذلك، سنقوم بتصور هذا السلوك لعدد من مؤشرات CV.

تصور مؤشرات التحقق المتقاطع للعديد من كائنات CV#

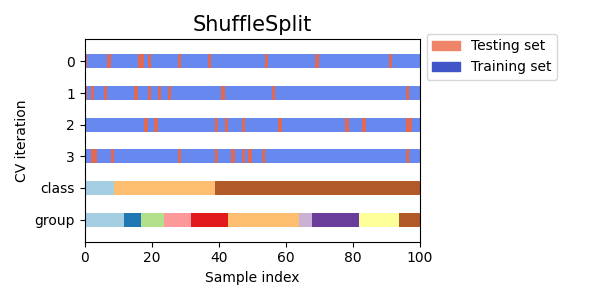
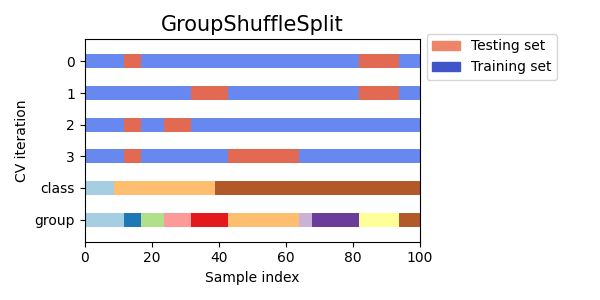
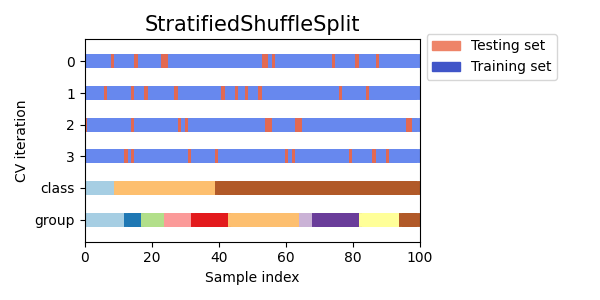
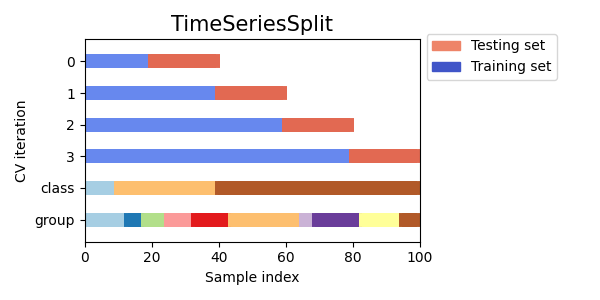
دعونا نقارن بصريًا سلوك التحقق المتقاطع للعديد من كائنات التحقق المتقاطع في سكايلرن. أدناه، سنقوم بالحلقة عبر العديد من كائنات التحقق المتقاطع الشائعة، وتصوير سلوك كل منها.

لاحظ كيف يستخدم البعض معلومات المجموعة/الفئة بينما لا يستخدمها الآخرون.

cvs = [
    KFold,
    GroupKFold,
    ShuffleSplit,
    StratifiedKFold,
    StratifiedGroupKFold,
    GroupShuffleSplit,
    StratifiedShuffleSplit,
    TimeSeriesSplit,
]


for cv in cvs:
    this_cv = cv(n_splits=n_splits)
    fig, ax = plt.subplots(figsize=(6, 3))
    plot_cv_indices(this_cv, X, y, groups, ax, n_splits)

    ax.legend(
        [Patch(color=cmap_cv(0.8)), Patch(color=cmap_cv(0.02))],
        ["Testing set", "Training set"],
        loc=(1.02, 0.8),
    )
    # ضبط الأسطورة
    plt.tight_layout()
    fig.subplots_adjust(right=0.7)
plt.show()