ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

# ======================================================== # المنحنيات المناسبة باستخدام الانحدار الخليط الخليط # ========================================================

# يحسب الانحدار الخليط الخليط للمنحنيات التوافقية.

# راجع انحدار ريدج البايزي لمزيد من المعلومات حول المنحني.

# بشكل عام، عند ملاءمة منحنى باستخدام متعدد الحدود بواسطة الانحدار الخليط الخليط، قد يكون اختيار القيم الأولية لمعاملات التنظيم (alpha، lambda) مهمًا. # هذا لأن معاملات التنظيم يتم تحديدها بواسطة إجراء تكراري يعتمد على القيم الأولية.

# في هذا المثال، يتم تقريب المنحنى التوافقي بواسطة متعدد الحدود باستخدام أزواج مختلفة من القيم الأولية.

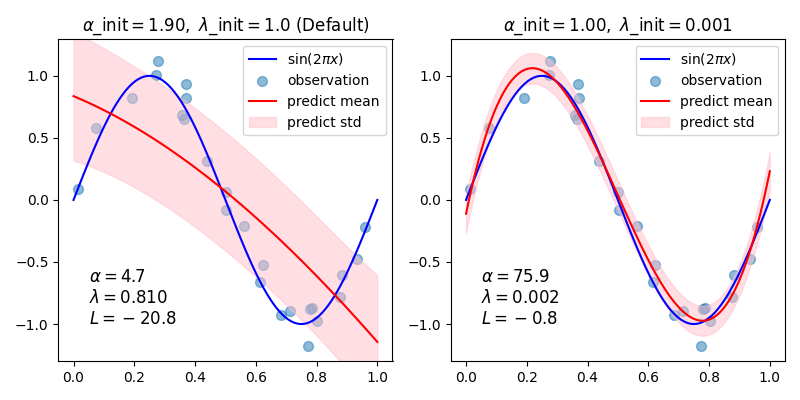
# عند البدء من القيم الافتراضية (alpha_init = 1.90, lambda_init = 1.)، يكون الانحياز للمنحنى الناتج كبيرًا، والتباين صغيرًا. # لذلك، يجب أن تكون lambda_init صغيرة نسبيًا (1.e-3) لتقليل الانحياز.

# أيضًا، من خلال تقييم الاحتمال الهامشي اللوغاريتمي (L) لهذه النماذج، يمكننا تحديد أيها أفضل. # يمكن الاستنتاج أن النموذج ذو L الأكبر أكثر احتمالًا.

توليد بيانات توافقية مع الضوضاء#

import numpy as np


def func(x):
    return np.sin(2 * np.pi * x)


size = 25
rng = np.random.RandomState(1234)
x_train = rng.uniform(0.0, 1.0, size)
y_train = func(x_train) + rng.normal(scale=0.1, size=size)
x_test = np.linspace(0.0, 1.0, 100)

الملاءمة بواسطة متعدد الحدود من الدرجة الثالثة#

from sklearn.linear_model import BayesianRidge

n_order = 3
X_train = np.vander(x_train, n_order + 1, increasing=True)
X_test = np.vander(x_test, n_order + 1, increasing=True)
reg = BayesianRidge(tol=1e-6, fit_intercept=False, compute_score=True)

رسم المنحنى الحقيقي والمتوقع مع الاحتمال الهامشي اللوغاريتمي (L)#

import matplotlib.pyplot as plt

fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for i, ax in enumerate(axes):
    # الانحدار الخليط الخليط مع أزواج مختلفة من القيم الأولية
    if i == 0:
        init = [1 / np.var(y_train), 1.0]  # القيم الافتراضية
    elif i == 1:
        init = [1.0, 1e-3]
        reg.set_params(alpha_init=init[0], lambda_init=init[1])
    reg.fit(X_train, y_train)
    ymean, ystd = reg.predict(X_test, return_std=True)

    ax.plot(x_test, func(x_test), color="blue", label="sin($2\\pi x$)")
    ax.scatter(x_train, y_train, s=50, alpha=0.5, label="observation")
    ax.plot(x_test, ymean, color="red", label="predict mean")
    ax.fill_between(
        x_test, ymean - ystd, ymean + ystd, color="pink", alpha=0.5, label="predict std"
    )
    ax.set_ylim(-1.3, 1.3)
    ax.legend()
    title = "$\\alpha$_init$={:.2f},\\ \\lambda$_init$={}$".format(init[0], init[1])
    if i == 0:
        title += " (Default)"
    ax.set_title(title, fontsize=12)
    text = "$\\alpha={:.1f}$\n$\\lambda={:.3f}$\n$L={:.1f}$".format(
        reg.alpha_, reg.lambda_, reg.scores_[-1]
    )
    ax.text(0.05, -1.0, text, fontsize=12)

plt.tight_layout()
plt.show()