ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

مقارنة بين اختبار F والمعلومات المتبادلة#

يوضح هذا المثال الاختلافات بين إحصائيات اختبار F أحادي المتغير والمعلومات المتبادلة.

نحن نعتبر 3 ميزات x_1 و x_2 و x_3 موزعة بشكل منتظم على [0، 1]، الهدف يعتمد عليها على النحو التالي:

y = x_1 + sin(6 * pi * x_2) + 0.1 * N(0, 1)، أي أن الميزة الثالثة غير ذات صلة تمامًا.

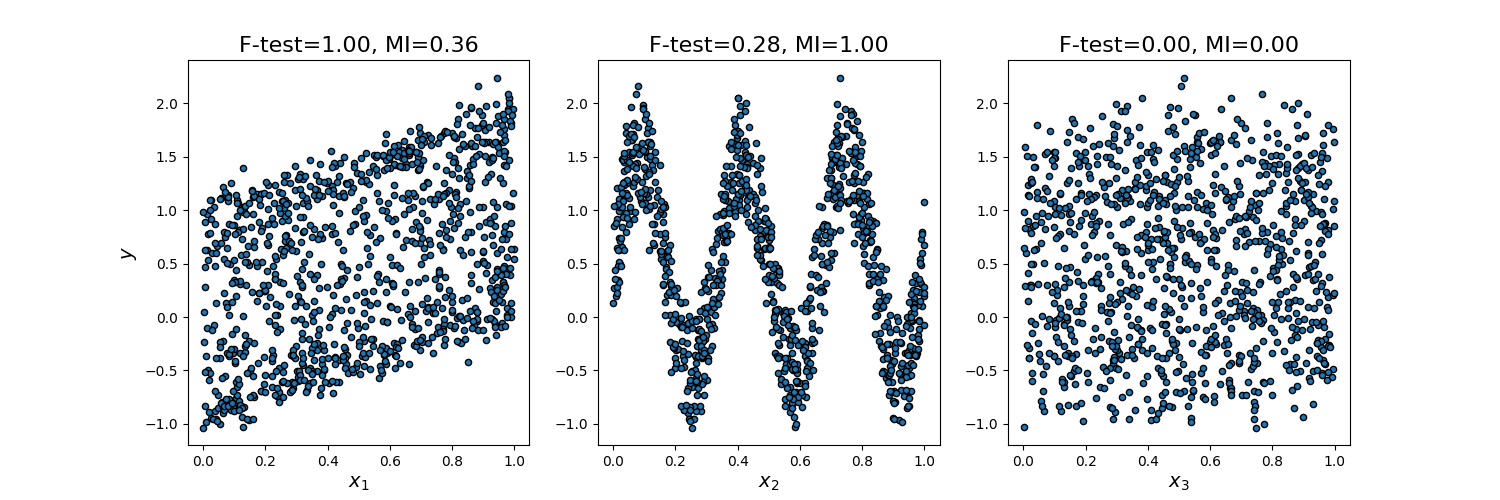
يعرض الكود أدناه اعتماد y مقابل x_i الفردية والقيم الطبيعية لإحصائيات اختبار F أحادي المتغير والمعلومات المتبادلة.

نظرًا لأن اختبار F يلتقط فقط التبعية الخطية، فإنه يصنف x_1 على أنها الميزة الأكثر تمييزًا. من ناحية أخرى، يمكن للمعلومات المتبادلة التقاط أي نوع من التبعية بين المتغيرات وتصنف x_2 على أنها الميزة الأكثر تمييزًا، مما يتفق على الأرجح بشكل أفضل مع إدراكنا الحدسي لهذا المثال. كلا الطريقتين تحدد x_3 بشكل صحيح على أنها غير ذات صلة.

F-test=1.00, MI=0.36, F-test=0.28, MI=1.00, F-test=0.00, MI=0.00

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.feature_selection import f_regression, mutual_info_regression

np.random.seed(0)
X = np.random.rand(1000, 3)
y = X[:, 0] + np.sin(6 * np.pi * X[:, 1]) + 0.1 * np.random.randn(1000)

f_test, _ = f_regression(X, y)
f_test /= np.max(f_test)

mi = mutual_info_regression(X, y)
mi /= np.max(mi)

plt.figure(figsize=(15, 5))
for i in range(3):
    plt.subplot(1, 3, i + 1)
    plt.scatter(X[:, i], y, edgecolor="black", s=20)
    plt.xlabel("$x_{}$".format(i + 1), fontsize=14)
    if i == 0:
        plt.ylabel("$y$", fontsize=14)
    plt.title("F-test={:.2f}, MI={:.2f}".format(f_test[i], mi[i]), fontsize=16)
plt.show()