ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

شجرة قرارات معززة متعددة الفئات#

هذا المثال يوضح كيف يمكن لتقنية التعزيز (Boosting) أن تحسن دقة التنبؤ في مشكلة تصنيف متعددة التصنيفات. وهو يعيد إنتاج تجربة مشابهة لما هو موضح في الشكل 1 في بحث Zhu et al [1].

المبدأ الأساسي لتقنية AdaBoost (Adaptive Boosting) هو ملاءمة تسلسل من المتعلمين الضعفاء (مثل شجرة القرارات) على نسخ معادة العينة من البيانات. يحمل كل عينة وزنًا يتم تعديله بعد كل خطوة تدريب، بحيث يتم تعيين أوزان أعلى للعينات المصنفة بشكل خاطئ. تأخذ عملية إعادة العينة بعين الاعتبار الأوزان المعينة لكل عينة. العينات ذات الأوزان الأعلى لديها فرصة أكبر للاختيار عدة مرات في مجموعة البيانات الجديدة، بينما العينات ذات الأوزان الأقل من المرجح أن يتم اختيارها. وهذا يضمن أن التركيز في الحلقات اللاحقة من الخوارزمية يكون على العينات التي يصعب تصنيفها.

المراجع

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

إنشاء مجموعة البيانات#

يتم إنشاء مجموعة بيانات التصنيف عن طريق أخذ توزيع طبيعي عشري الأبعاد (\(x\) in \(R^{10}\)) وتحديد ثلاث فئات مفصولة بكرات عشرية الأبعاد متداخلة ومتمركزة بحيث يكون هناك أعداد متساوية تقريبًا من العينات في كل فئة (الكميات المئوية لتوزيع \(\chi^2\)).

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.dummy import DummyClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_gaussian_quantiles

X, y = make_gaussian_quantiles(
    n_samples=2_000, n_features=10, n_classes=3, random_state=1
)

نقسم مجموعة البيانات إلى مجموعتين: 70% من العينات تستخدم للتدريب و30% المتبقية للاختبار.

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=0.7, random_state=42
)

تدريب `AdaBoostClassifier`#

نقوم بتدريب AdaBoostClassifier. يستخدم هذا التقدير تقنية التعزيز (Boosting) لتحسين دقة التصنيف. التعزيز هي طريقة مصممة لتدريب المتعلمين الضعفاء (أي estimator) الذين يتعلمون من أخطاء أسلافهم.

هنا، نحدد المتعلم الضعيف كـ DecisionTreeClassifier ونحدد العدد الأقصى للأوراق إلى 8. في الإعداد الحقيقي، يجب ضبط هذا المعامل. نضبطه على قيمة منخفضة إلى حد ما للحد من وقت تشغيل المثال.

يستخدم خوارزمية SAMME المدمجة في AdaBoostClassifier التنبؤات الصحيحة أو الخاطئة التي يقوم بها المتعلم الضعيف الحالي لتحديث أوزان العينات المستخدمة لتدريب المتعلمين الضعفاء المتتاليين. أيضًا، يتم حساب وزن المتعلم الضعيف نفسه بناءً على دقته في تصنيف الأمثلة التدريبية. يحدد وزن المتعلم الضعيف تأثيره على التنبؤ النهائي للمجموعة.

weak_learner = DecisionTreeClassifier(max_leaf_nodes=8)
n_estimators = 300

adaboost_clf = AdaBoostClassifier(
    estimator=weak_learner,
    n_estimators=n_estimators,
    random_state=42,
).fit(X_train, y_train)
adaboost_clf = AdaBoostClassifier(
    estimator=weak_learner,
    n_estimators=n_estimators,
    random_state=42,
).fit(X_train, y_train)

التحليل#

تقارب `AdaBoostClassifier`#

لإظهار فعالية التعزيز في تحسين الدقة، نقوم بتقييم خطأ التصنيف الخاطئ للأشجار المعززة مقارنة بنقطتين مرجعيتين. النتيجة المرجعية الأولى هي misclassification_error التي تم الحصول عليها من متعلم ضعيف واحد (أي DecisionTreeClassifier)، والتي تخدم كنقطة مرجعية. النتيجة المرجعية الثانية يتم الحصول عليها من DummyClassifier، والذي يتنبأ بالفئة الأكثر شيوعًا في مجموعة البيانات.

dummy_clf = DummyClassifier()


def misclassification_error(y_true, y_pred):
    return 1 - accuracy_score(y_true, y_pred)


weak_learners_misclassification_error = misclassification_error(
    y_test, weak_learner.fit(X_train, y_train).predict(X_test)
)

dummy_classifiers_misclassification_error = misclassification_error(
    y_test, dummy_clf.fit(X_train, y_train).predict(X_test)
)

print(
    "DecisionTreeClassifier's misclassification_error: "
    f"{weak_learners_misclassification_error:.3f}"
)
print(
    "DummyClassifier's misclassification_error: "
    f"{dummy_classifiers_misclassification_error:.3f}"
)

DecisionTreeClassifier's misclassification_error: 0.475
DummyClassifier's misclassification_error: 0.692

بعد تدريب نموذج DecisionTreeClassifier، يتجاوز الخطأ القيمة المتوقعة التي كان من المفترض الحصول عليها من خلال تخمين تسمية الفئة الأكثر شيوعًا، كما يفعل DummyClassifier.

الآن، نقوم بحساب misclassification_error، أي 1 - accuracy، للنموذج الإضافي (DecisionTreeClassifier) في كل حلقات التعزيز على مجموعة الاختبار لتقييم أدائه.

نستخدم staged_predict الذي يقوم بعدد من الحلقات يساوي عدد التقديرات المجهزة (أي المقابلة لـ n_estimators). في الحلقة n، تستخدم تنبؤات AdaBoost فقط n من المتعلمين الضعفاء الأوائل. نقارن هذه التنبؤات مع التنبؤات الصحيحة y_test وبالتالي نستنتج فائدة (أو عدم فائدة) إضافة متعلم ضعيف جديد إلى السلسلة.

نرسم خطأ التصنيف الخاطئ للمراحل المختلفة:

boosting_errors = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "AdaBoost": [
            misclassification_error(y_test, y_pred)
            for y_pred in adaboost_clf.staged_predict(X_test)
        ],
    }
).set_index("Number of trees")
ax = boosting_errors.plot()
ax.set_ylabel("Misclassification error on test set")
ax.set_title("Convergence of AdaBoost algorithm")

plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [weak_learners_misclassification_error, weak_learners_misclassification_error],
    color="tab:orange",
    linestyle="dashed",
)
plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [
        dummy_classifiers_misclassification_error,
        dummy_classifiers_misclassification_error,
    ],
    color="c",
    linestyle="dotted",
)
plt.legend(["AdaBoost", "DecisionTreeClassifier", "DummyClassifier"], loc=1)
plt.show()

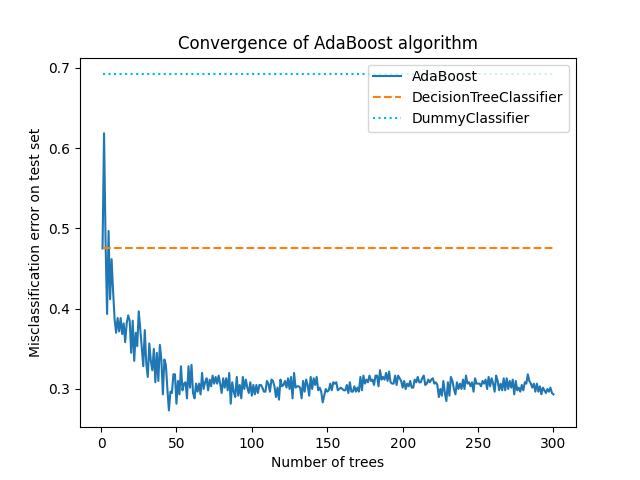
يوضح الرسم البياني خطأ التصنيف الخاطئ على مجموعة الاختبار بعد كل حلقات التعزيز. نرى أن خطأ الأشجار المعززة يتقارب إلى خطأ حوالي 0.3 بعد 50 حلقات، مما يشير إلى دقة أعلى بشكل ملحوظ مقارنة بشجرة واحدة، كما يوضح الخط المتقطع في الرسم البياني.

يتذبذب خطأ التصنيف الخاطئ لأن خوارزمية SAMME تستخدم المخرجات المنفصلة للمتعلمين الضعفاء لتدريب النموذج المعزز.

يتأثر تقارب AdaBoostClassifier بشكل أساسي بمعدل التعلم (أي learning_rate)، وعدد المتعلمين الضعفاء المستخدمين (n_estimators)، وقدرة التعبير للمتعلمين الضعفاء (مثل max_leaf_nodes).

أخطاء وأوزان المتعلمين الضعفاء#

كما ذكرنا سابقًا، AdaBoost هو نموذج إضافي مرحلي للأمام. الآن، نركز على فهم العلاقة بين الأوزان المنسوبة للمتعلمين الضعفاء وأدائهم الإحصائي.

نستخدم سمات AdaBoostClassifier المجهزة estimator_errors_ و`estimator_weights_` لاستكشاف هذه العلاقة.

weak_learners_info = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "Errors": adaboost_clf.estimator_errors_,
        "Weights": adaboost_clf.estimator_weights_,
    }
).set_index("Number of trees")

axs = weak_learners_info.plot(
    subplots=True, layout=(1, 2), figsize=(10, 4), legend=False, color="tab:blue"
)
axs[0, 0].set_ylabel("Train error")
axs[0, 0].set_title("Weak learner's training error")
axs[0, 1].set_ylabel("Weight")
axs[0, 1].set_title("Weak learner's weight")
fig = axs[0, 0].get_figure()
fig.suptitle("Weak learner's errors and weights for the AdaBoostClassifier")
fig.tight_layout()

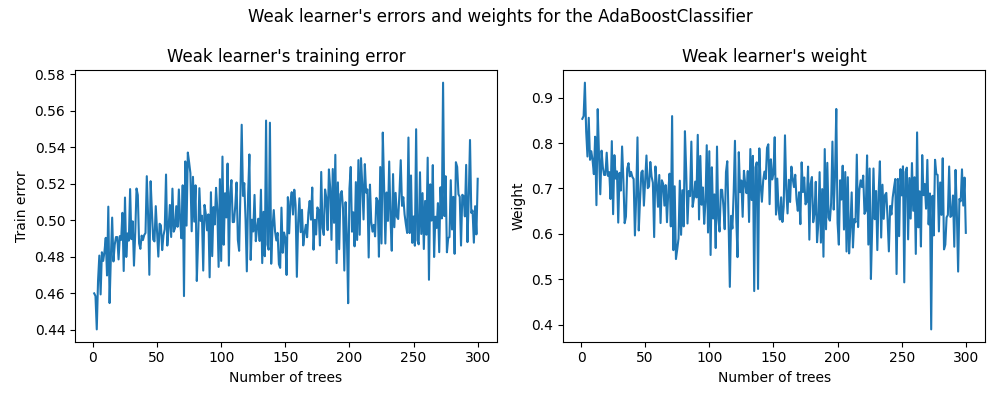
Weak learner's errors and weights for the AdaBoostClassifier, Weak learner's training error, Weak learner's weight

في الرسم البياني الأيسر، نعرض خطأ كل متعلم ضعيف على مجموعة التدريب المعاد وزنها في كل حلقات التعزيز. في الرسم البياني الأيمن، نعرض الأوزان المرتبطة بكل متعلم ضعيف والتي تستخدم لاحقًا لإجراء تنبؤات النموذج الإضافي النهائي.

نرى أن خطأ المتعلم الضعيف هو عكس الأوزان. هذا يعني أن نموذجنا الإضافي سيثق أكثر بمتعلم ضعيف يقوم بأخطاء أصغر (على مجموعة التدريب) عن طريق زيادة تأثيره على القرار النهائي. في الواقع، هذه هي صيغة تحديث أوزان التقديرات الأساسية بعد كل حلقات في AdaBoost.

ملاحظة أخرى مثيرة للاهتمام هي أن المتعلمين الضعفاء الأوائل للنموذج يقومون بأخطاء أقل من المتعلمين الضعفاء اللاحقين في سلسلة التعزيز.

الحدس وراء هذه الملاحظة هو التالي: بسبب إعادة وزن العينات، يتم إجبار المتعلمين اللاحقين على محاولة تصنيف العينات الأكثر صعوبة أو ضوضاء وتجاهل العينات المصنفة بالفعل بشكل جيد. لذلك، سيزداد الخطأ الإجمالي على مجموعة التدريب. ولهذا السبب يتم بناء أوزان المتعلم الضعيف لموازنة المتعلمين الضعفاء ذوي الأداء الأسوأ.

Total running time of the script: (0 minutes 8.630 seconds)