ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تعديل الفرصة في تقييم أداء التجميع#

يستكشف هذا الدفتر تأثير التصنيف العشوائي الموزع بشكل موحد على سلوك بعض مقاييس تقييم التجميع. لهذا الغرض، يتم حساب المقاييس بعدد ثابت من العينات ودالة لعدد التجمعات التي يعينها المقدر. وينقسم المثال إلى تجربتين:

تجربة أولى مع "علامات الحقيقة الأرضية" الثابتة (وبالتالي عدد ثابت من الفئات) و"علامات متوقعة" عشوائية؛
تجربة ثانية مع "علامات الحقيقة الأرضية" المتغيرة، "علامات متوقعة" عشوائية. تحتوي "العلامات المتوقعة" على نفس عدد الفئات والتجمعات مثل "علامات الحقيقة الأرضية".

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

تحديد قائمة المقاييس لتقييمها#

خوارزميات التجميع هي أساليب تعلم غير خاضعة للإشراف بشكل أساسي. ومع ذلك، نظرًا لأننا نعين علامات الفئات للتجمعات الاصطناعية في هذا المثال، فمن الممكن استخدام مقاييس التقييم التي تستفيد من هذه معلومات "الإشراف" الحقيقة الأرضية لقياس جودة التجمعات الناتجة المجموعات. أمثلة على هذه المقاييس هي ما يلي:

V-measure، المتوسط التوافقي للاكتمال والتماثل؛
Rand index، الذي يقيس مدى تكرار أزواج نقاط البيانات التي يتم تجميعها باستمرار وفقًا لنتيجة خوارزمية التجميع وتعيين فئة الحقيقة الأرضية؛
مؤشر Rand المعدل (ARI)، وهو مؤشر Rand المعدل بحيث يكون تعيين التجميع العشوائي لديه ARI من 0.0 في التوقع؛
معلومات متبادلة (MI) هي مقياس نظري للمعلومات يحدد مدى الاعتماد التسميات. لاحظ أن القيمة القصوى لـ MI للتسميات المثالية تعتمد على عدد التجمعات والعينات؛
معلومات متبادلة طبيعية (NMI)، معلومات متبادلة محددة بين 0 (لا توجد معلومات متبادلة) في حد عدد كبير من نقاط البيانات و 1 (تعيينات التسميات المطابقة تمامًا، حتى ترتيب التسميات). لا يتم تعديله للفرصة: ثم إذا لم يكن عدد نقاط البيانات المجمعة كبيرًا بما يكفي، فإن القيم المتوقعة لـ MI أو NMI للتسميات العشوائية يمكن أن تكون كبيرة بشكل كبير وغير صفرية؛
معلومات متبادلة معدلة (AMI)، معلومات متبادلة معدلة. على غرار ARI، فإن تعيين التجميع العشوائي لديه AMI من 0.0 في التوقع.

للحصول على مزيد من المعلومات، راجع وحدة التقييم :ref: clustering_evaluation.

from sklearn import metrics

score_funcs = [
    ("V-measure", metrics.v_measure_score),
    ("Rand index", metrics.rand_score),
    ("ARI", metrics.adjusted_rand_score),
    ("MI", metrics.mutual_info_score),
    ("NMI", metrics.normalized_mutual_info_score),
    ("AMI", metrics.adjusted_mutual_info_score),
]

التجربة الأولى: علامات الحقيقة الأرضية الثابتة وعدد متزايد من التجمعات#

نحن نحدد أولاً دالة تخلق التصنيف العشوائي الموزع بشكل موحد.

import numpy as np

rng = np.random.RandomState(0)

def random_labels(n_samples, n_classes):
    return rng.randint(low=0, high=n_classes, size=n_samples)

ستستخدم دالة أخرى دالة random_labels لإنشاء مجموعة ثابتة من علامات الحقيقة الأرضية (labels_a) الموزعة في n_classes ثم تسجيل عدة مجموعات من العلامات "المتوقعة" عشوائيًا (labels_b) لتقييم تقلب مقياس معين عند n_clusters معين.

def fixed_classes_uniform_labelings_scores(
    score_func, n_samples, n_clusters_range, n_classes, n_runs=5
):
    scores = np.zeros((len(n_clusters_range), n_runs))
    labels_a = random_labels(n_samples=n_samples, n_classes=n_classes)
    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

في هذا المثال الأول، نحدد عدد الفئات (العدد الحقيقي للتجمعات) إلى n_classes=10. يختلف عدد التجمعات عبر القيم المقدمة بواسطة n_clusters_range.

import matplotlib.pyplot as plt
import seaborn as sns

n_samples = 1000
n_classes = 10
n_clusters_range = np.linspace(2, 100, 10).astype(int)
plots = []
names = []

sns.color_palette("colorblind")
plt.figure(1)

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = fixed_classes_uniform_labelings_scores(
        score_func, n_samples, n_clusters_range, n_classes=n_classes
    )
    plots.append(
        plt.errorbar(
            n_clusters_range,
            scores.mean(axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=1,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "Clustering measures for random uniform labeling\n"
    f"against reference assignment with {n_classes} classes"
)
plt.xlabel(f"Number of clusters (Number of samples is fixed to {n_samples})")
plt.ylabel("Score value")
plt.ylim(bottom=-0.05, top=1.05)
plt.legend(plots, names, bbox_to_anchor=(0.5, 0.5))
plt.show()

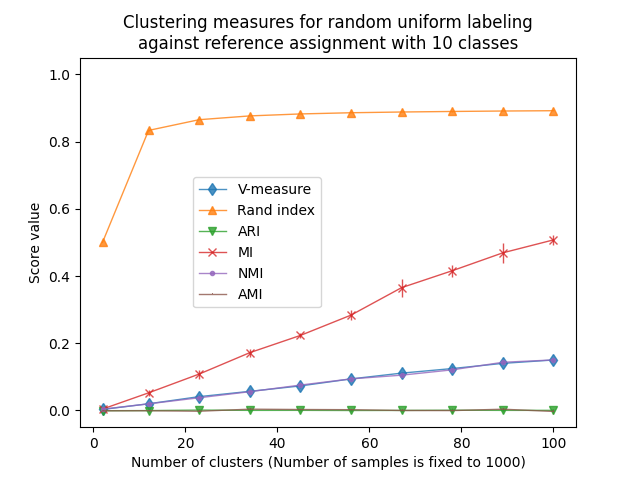
Clustering measures for random uniform labeling against reference assignment with 10 classes

يتشبع مؤشر Rand لـ n_clusters > n_classes. المقاييس الأخرى غير المعدلة مثل V-Measure التي تظهر اعتمادًا خطيًا بين عدد التجمعات وعدد العينات.

مقياس معدلة للفرصة، مثل ARI وAMI، تعرض بعض التباين العشوائي حول متوسط النتيجة 0.0، بغض النظر عن عدد العينات والتجمعات.

التجربة الثانية: عدد متغير من الفئات والتجمعات#

في هذا القسم، نحدد دالة مماثلة تستخدم عدة مقاييس لتسجيل 2 تسميات عشوائية موزعة بشكل موحد. في هذه الحالة، يتم مطابقة عدد الفئات وعدد التجمعات المعينة لكل قيمة ممكنة في n_clusters_range.

def uniform_labelings_scores(score_func, n_samples, n_clusters_range, n_runs=5):
    scores = np.zeros((len(n_clusters_range), n_runs))

    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_a = random_labels(n_samples=n_samples, n_classes=n_clusters)
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

في هذه الحالة، نستخدم n_samples=100 لإظهار تأثير وجود عدد من التجمعات مماثلة أو متساوية لعدد العينات.

n_samples = 100
n_clusters_range = np.linspace(2, n_samples, 10).astype(int)

plt.figure(2)

المخططات = []
الأسماء = []

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = uniform_labelings_scores(score_func, n_samples, n_clusters_range)
    plots.append(
        plt.errorbar(
            n_clusters_range,
            np.median(scores, axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=2,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "مقاييس التجميع لتسميتين عشوائيتين موحدتين\nمع عدد متساوٍ من التجمعات"
)
plt.xlabel(f"عدد التجمعات (عدد العينات ثابت عند {n_samples})")
plt.ylabel("قيمة النتيجة")
plt.legend(plots, names)
plt.ylim(bottom=-0.05, top=1.05)
plt.show()

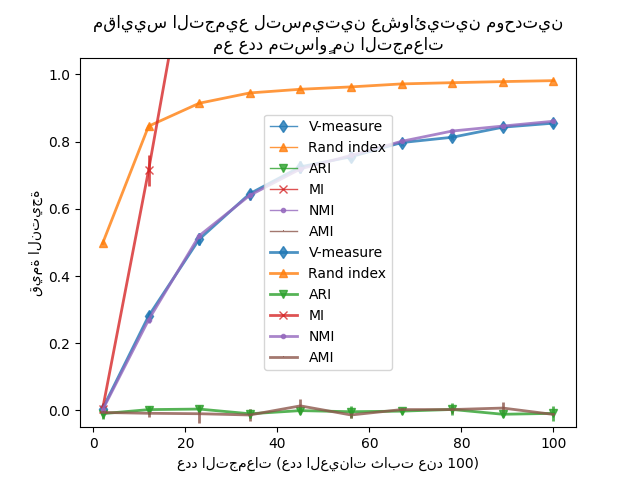
مقاييس التجميع لتسميتين عشوائيتين موحدتين مع عدد متساوٍ من التجمعات

نلاحظ نتائج مماثلة للتجربة الأولى: المقاييس المعدلة للفرصة تظل ثابتة بالقرب من الصفر بينما تميل المقاييس الأخرى إلى أن تصبح أكبر مع التسميات الدقيقة. متوسط V-measure للتسمية العشوائية يزيد بشكل كبير حيث يكون عدد التجمعات أقرب إلى العدد الإجمالي العينات المستخدمة لحساب المقياس. علاوة على ذلك، فإن المعلومات المتبادلة الخام غير محدودة من الأعلى ونطاقها يعتمد على أبعاد مشكلة التجميع وتكافؤ فئات الحقيقة الأرضية. هذا هو السبب في المنحنى يخرج من المخطط.

يمكن استخدام المقاييس المعدلة فقط بأمان كمؤشر توافق لتقييم استقرار متوسط خوارزميات التجميع لقيمة معينة من k على عينات فرعية متداخلة مختلفة من مجموعة البيانات.

يمكن أن تكون مقاييس تقييم التجميع غير المعدلة مضللة لأنها إخراج قيم كبيرة للتسميات الدقيقة، يمكن للمرء أن يقود التفكير أن التسمية قد أسرت مجموعات ذات معنى بينما يمكن أن تكون عشوائية تمامًا. على وجه الخصوص، لا ينبغي استخدام مثل هذه المقاييس غير المعدلة لمقارنة نتائج خوارزميات التجميع المختلفة التي تخرج عددًا مختلفًا التجمعات.

Total running time of the script: (0 minutes 1.331 seconds)