ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
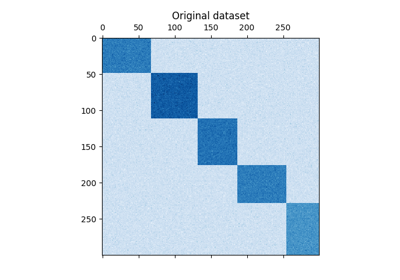
# =========================================== # التجميع الطيفي لتجزئة الصور # ===========================================
في هذا المثال، يتم توليد صورة بدوائر متصلة ويتم استخدام التجميع الطيفي لفصل الدوائر.
في هذه الإعدادات، يحل نهج التجميع الطيفي المشكلة المعروفة باسم "القطع الرسومية المعيارية": حيث يتم النظر إلى الصورة على أنها رسم بياني للبكسلات المتصلة، وتتمثل خوارزمية التجميع الطيفي في اختيار القطع الرسومية التي تحدد المناطق مع تقليل نسبة التدرج على طول القطع وحجم المنطقة.
وبما أن الخوارزمية تحاول موازنة الحجم (أي موازنة أحجام المناطق)، إذا أخذنا دوائر بأحجام مختلفة، فإن التجزئة تفشل.
بالإضافة إلى ذلك، نظرًا لعدم وجود معلومات مفيدة في شدة الصورة أو تدرجها، فإننا نختار إجراء التجميع الطيفي على رسم بياني يتم إعلامه بشكل ضعيف فقط بالتدرج. وهذا قريب من إجراء تقسيم فورونوي للرسم البياني.
بالإضافة إلى ذلك، نستخدم قناع الأجسام لتقييد الرسم البياني إلى مخطط الأجسام. في هذا المثال، نحن مهتمون بفصل الأجسام عن بعضها البعض، وليس عن الخلفية.
# المؤلفون: مطوري سكايت-ليرن
# معرف رخصة SPDX: BSD-3-Clause
توليد البيانات#
from sklearn.cluster import spectral_clustering
import matplotlib.pyplot as plt
from sklearn.feature_extraction import image
import numpy as np
l = 100
x, y = np.indices((l, l))
center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)
radius1, radius2, radius3, radius4 = 16, 14, 15, 14
circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1**2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2**2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3**2
circle4 = (x - center4[0]) ** 2 + (y - center4[1]) ** 2 < radius4**2
رسم أربعة دوائر#
img = circle1 + circle2 + circle3 + circle4
# نستخدم قناعًا يحد من المقدمة: المشكلة التي نهتم بها هنا ليست فصل الأجسام عن الخلفية،
# ولكن فصلها عن بعضها البعض.
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
تحويل الصورة إلى رسم بياني مع قيمة التدرج على الحواف.
graph = image.img_to_graph(img, mask=mask)
خذ دالة متناقصة من التدرج مما يؤدي إلى تجزئة قريبة من تقسيم فورونوي
graph.data = np.exp(-graph.data / graph.data.std())
هنا نقوم بالتجميع الطيفي باستخدام محلح arpack لأن amg غير مستقر رقميا في هذا المثال. ثم نقوم برسم النتائج.
labels = spectral_clustering(graph, n_clusters=4, eigen_solver="arpack")
label_im = np.full(mask.shape, -1.0)
label_im[mask] = labels
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
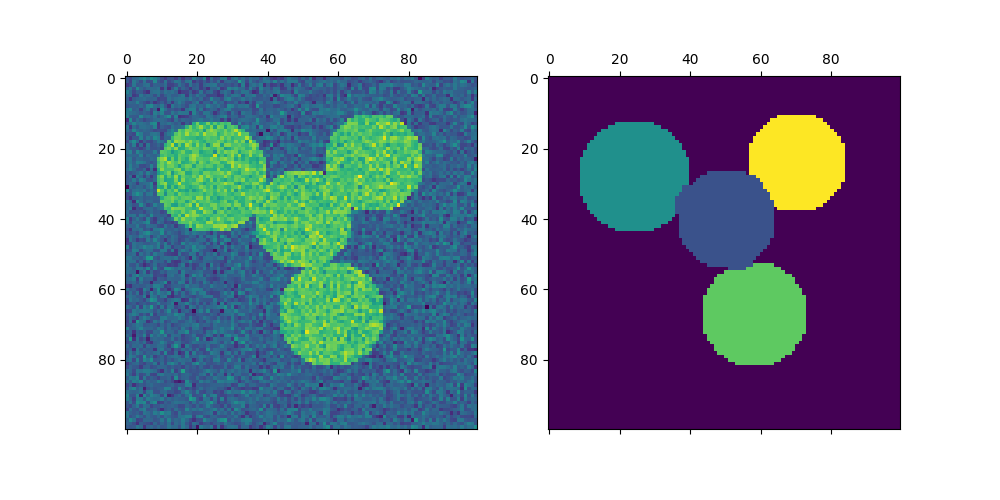
axs[0].matshow(img)
axs[1].matshow(label_im)
plt.show()
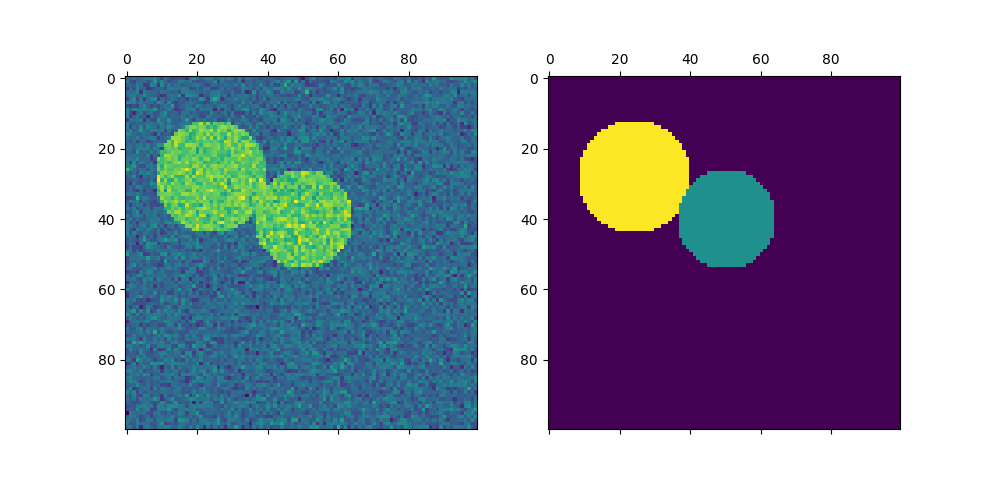
رسم دائرتين#
هنا نكرر العملية أعلاه ولكن نأخذ في الاعتبار الدائرتين الأوليين فقط قمنا بتوليدهما. لاحظ أن هذا يؤدي إلى فصل أنظف بين الدوائر حيث يسهل موازنة أحجام المناطق في هذه الحالة.
img = circle1 + circle2
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
labels = spectral_clustering(graph, n_clusters=2, eigen_solver="arpack")
label_im = np.full(mask.shape, -1.0)
label_im[mask] = labels
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
axs[0].matshow(img)
axs[1].matshow(label_im)
plt.show()
Total running time of the script: (0 minutes 0.803 seconds)
Related examples
sphx_glr_auto_examples_applications_plot_tomography_l1_reconstruction.py