ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
# التجميع التجميعي مع مقاييس مختلفة#
توضح تأثير مقاييس مختلفة على التجميع الهرمي.
تم تصميم المثال لإظهار تأثير اختيار مقاييس مختلفة. يتم تطبيقه على الموجات، والتي يمكن اعتبارها متجهًا عالي الأبعاد. في الواقع، يكون الفرق بين المقاييس أكثر وضوحًا في الأبعاد العالية (خاصة بالنسبة للمقاييس الإقليدية والمدينة).
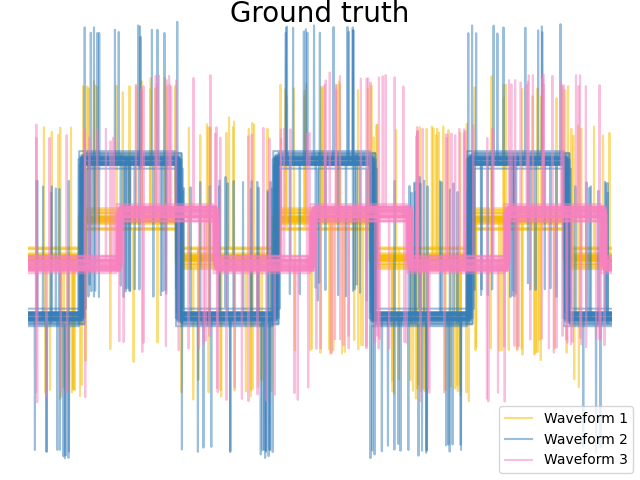
نحن نولد البيانات من ثلاث مجموعات من الموجات. اثنان من الموجات (الموجة 1 والموجة 2) متناسبان مع بعضهما البعض. المسافة المثلثية ثابتة بالنسبة لقياس البيانات، ونتيجة لذلك، لا يمكنها التمييز بين هاتين الموجتين. وبالتالي، حتى بدون ضوضاء، فإن التجميع باستخدام هذه المسافة لن يفصل الموجة 1 والموجة 2.
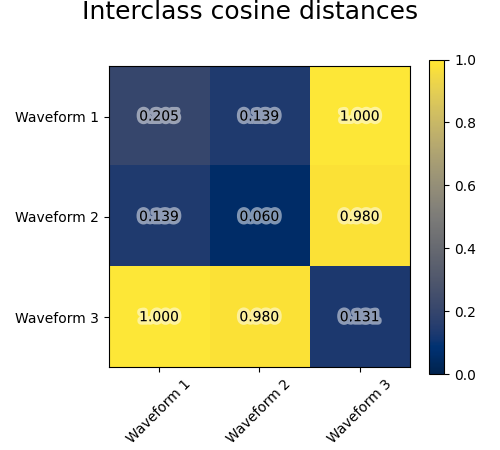
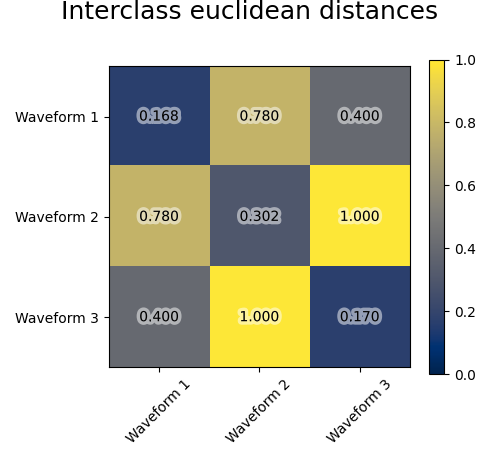
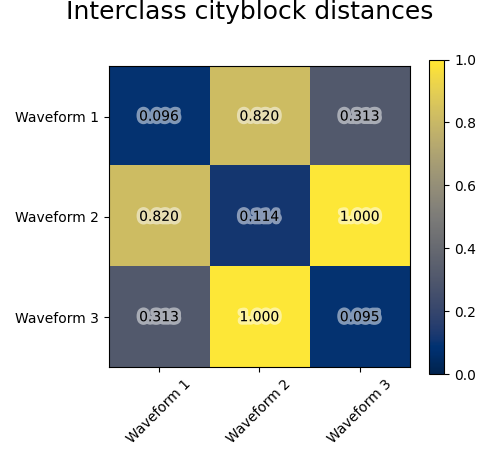
نضيف ضوضاء الملاحظة إلى هذه الموجات. نولد ضوضاء نادرة جدًا: تحتوي 6% فقط من نقاط الوقت على ضوضاء. ونتيجة لذلك، فإن المعيار l1 لهذه الضوضاء (أي مسافة "المدينة") أصغر بكثير من المعيار l2 ("المسافة الإقليدية"). يمكن ملاحظة ذلك على مصفوفات المسافة بين الفئات: القيم على القطر، التي تميز انتشار الفئة، أكبر بكثير للمسافة الإقليدية من مسافة المدينة.
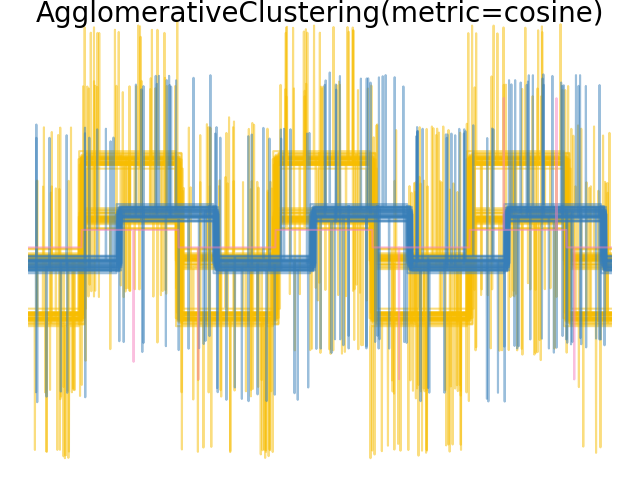
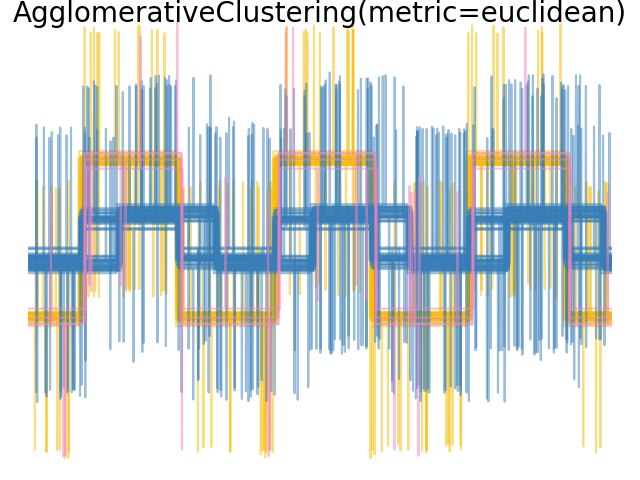
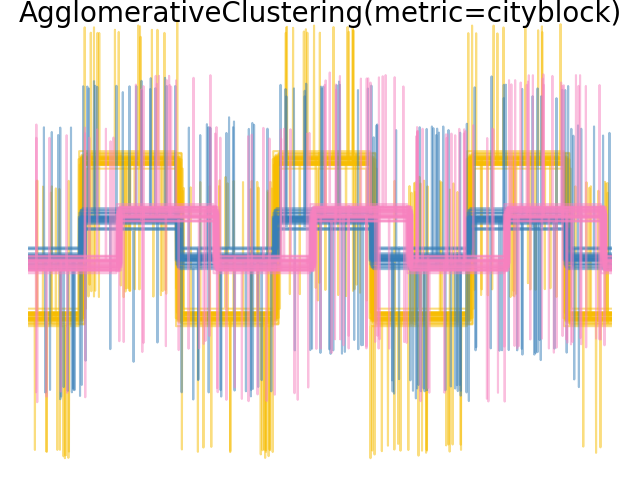
عندما نطبق التجميع على البيانات، نجد أن التجميع يعكس ما كان في مصفوفات المسافة. في الواقع، بالنسبة للمسافة الإقليدية، فإن الفئات غير منفصلة جيدًا بسبب الضوضاء، وبالتالي فإن التجميع لا يفصل الموجات. بالنسبة للمسافة بين المدن، يكون الفصل جيدًا ويتم استرداد فئات الموجات. أخيرًا، لا تفصل المسافة المثلثية على الإطلاق الموجة 1 والموجة 2، وبالتالي فإن التجميع يضعها في نفس المجموعة.
# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause
import matplotlib.patheffects as PathEffects
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distances
np.random.seed(0)
# توليد بيانات الموجة
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)
def sqr(x):
return np.sign(np.cos(x))
X = list()
y = list()
for i, (phi, a) in enumerate([(0.5, 0.15), (0.5, 0.6), (0.3, 0.2)]):
for _ in range(30):
phase_noise = 0.01 * np.random.normal()
amplitude_noise = 0.04 * np.random.normal()
additional_noise = 1 - 2 * np.random.rand(n_features)
# جعل الضوضاء نادرة
additional_noise[np.abs(additional_noise) < 0.997] = 0
X.append(
12
* (
(a + amplitude_noise) * (sqr(6 * (t + phi + phase_noise)))
+ additional_noise
)
)
y.append(i)
X = np.array(X)
y = np.array(y)
n_clusters = 3
labels = ("Waveform 1", "Waveform 2", "Waveform 3")
colors = ["#f7bd01", "#377eb8", "#f781bf"]
# رسم التصنيف الحقيقي
plt.figure()
plt.axes([0, 0, 1, 1])
for l, color, n in zip(range(n_clusters), colors, labels):
lines = plt.plot(X[y == l].T, c=color, alpha=0.5)
lines[0].set_label(n)
plt.legend(loc="best")
plt.axis("tight")
plt.axis("off")
plt.suptitle("Ground truth", size=20, y=1)
# رسم المسافات
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
avg_dist = np.zeros((n_clusters, n_clusters))
plt.figure(figsize=(5, 4.5))
for i in range(n_clusters):
for j in range(n_clusters):
avg_dist[i, j] = pairwise_distances(
X[y == i], X[y == j], metric=metric
).mean()
avg_dist /= avg_dist.max()
for i in range(n_clusters):
for j in range(n_clusters):
t = plt.text(
i,
j,
"%5.3f" % avg_dist[i, j],
verticalalignment="center",
horizontalalignment="center",
)
t.set_path_effects(
[PathEffects.withStroke(
linewidth=5, foreground="w", alpha=0.5)]
)
plt.imshow(avg_dist, interpolation="nearest", cmap="cividis", vmin=0)
plt.xticks(range(n_clusters), labels, rotation=45)
plt.yticks(range(n_clusters), labels)
plt.colorbar()
plt.suptitle("Interclass %s distances" % metric, size=18, y=1)
plt.tight_layout()
# رسم نتائج التجميع
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
model = AgglomerativeClustering(
n_clusters=n_clusters, linkage="average", metric=metric
)
model.fit(X)
plt.figure()
plt.axes([0, 0, 1, 1])
for l, color in zip(np.arange(model.n_clusters), colors):
plt.plot(X[model.labels_ == l].T, c=color, alpha=0.5)
plt.axis("tight")
plt.axis("off")
plt.suptitle("AgglomerativeClustering(metric=%s)" % metric, size=20, y=1)
plt.show()
Total running time of the script: (0 minutes 1.207 seconds)
Related examples
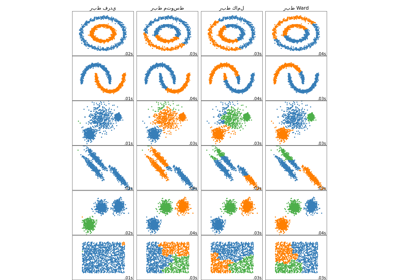
مقارنة طرق الربط الهرمي المختلفة على مجموعات بيانات تجريبية