ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

معايرة احتمالات المصنفات#

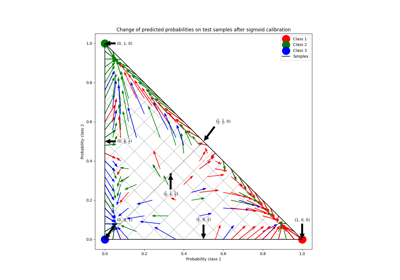
عند إجراء التصنيف، غالبًا ما تريد التنبؤ ليس فقط بتسمية الفئة، ولكن أيضًا الاحتمالية المرتبطة بها. هذه الاحتمالية تعطيك نوعًا من الثقة في التنبؤ. ومع ذلك، لا توفر جميع المصنفات احتمالات معايرة جيدًا، بعضها مفرط الثقة في حين أن البعض الآخر غير واثق. لذلك، غالبًا ما تكون معايرة الاحتمالات المتوقعة مرغوبة كعملية ما بعد المعالجة. يوضح هذا المثال طريقتان مختلفتان لهذه المعايرة ويقيم جودة الاحتمالات المعادة باستخدام درجة Brier (انظر https://en.wikipedia.org/wiki/Brier_score).

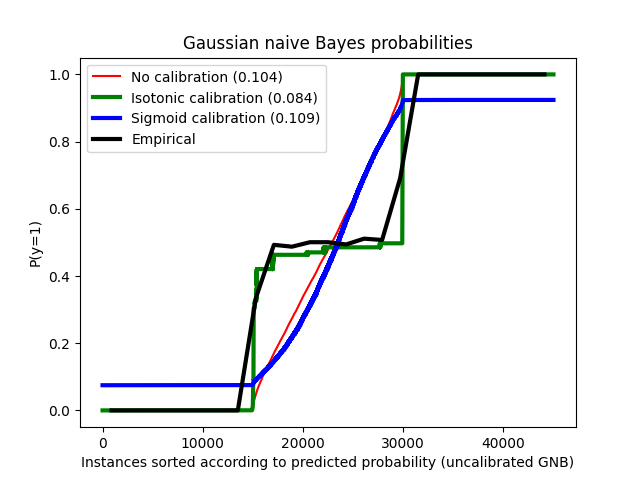
يتم مقارنة الاحتمالية المقدرة باستخدام مصنف خوارزمية بايز الساذجة الغاوسية دون معايرة، مع معايرة سيجمويد، ومع معايرة غير معلمية إيزوتونية. يمكن ملاحظة أن النموذج غير المعلمي فقط هو قادر على توفير معايرة احتمالية تعيد احتمالات قريبة من المتوقع 0.5 لمعظم العينات التي تنتمي إلى المجموعة الوسطى مع تسميات متغايرة. يؤدي هذا إلى تحسن كبير في درجة Brier.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

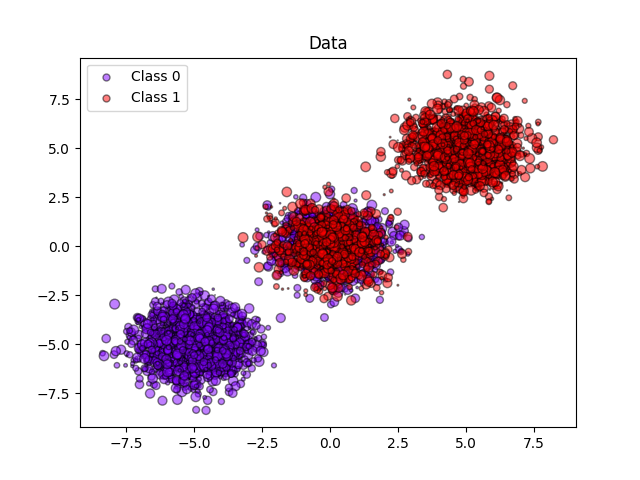
إنشاء مجموعة بيانات اصطناعية#

from matplotlib import cm
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import brier_score_loss
from sklearn.calibration import CalibratedClassifierCV
import numpy as np

from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split

n_samples = 50000
n_bins = 3  # استخدم 3 صناديق لمعايرة المنحنى حيث لدينا 3 مجموعات هنا

# إنشاء 3 مجموعات مع فئتين حيث تحتوي المجموعة الثانية على
# نصف العينات الإيجابية ونصف العينات السلبية. الاحتمالية في هذه
# المجموعة هي 0.5.
centers = [(-5, -5), (0, 0), (5, 5)]
X, y = make_blobs(n_samples=n_samples, centers=centers,
                  shuffle=False, random_state=42)

y[: n_samples // 2] = 0
y[n_samples // 2:] = 1
sample_weight = np.random.RandomState(42).rand(y.shape[0])

# تقسيم البيانات إلى مجموعات التدريب والاختبار للمعايرة
X_train, X_test, y_train, y_test, sw_train, sw_test = train_test_split(
    X, y, sample_weight, test_size=0.9, random_state=42
)

خوارزمية بايز الساذجة الغاوسية#

# بدون معايرة
clf = GaussianNB()
# خوارزمية بايز الساذجة الغاوسية نفسها لا تدعم الأوزان العشوائية
clf.fit(X_train, y_train)
prob_pos_clf = clf.predict_proba(X_test)[:, 1]

# مع معايرة إيزوتونية
clf_isotonic = CalibratedClassifierCV(clf, cv=2, method="isotonic")
clf_isotonic.fit(X_train, y_train, sample_weight=sw_train)
prob_pos_isotonic = clf_isotonic.predict_proba(X_test)[:, 1]

# مع معايرة سيجمويد
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method="sigmoid")
clf_sigmoid.fit(X_train, y_train, sample_weight=sw_train)
prob_pos_sigmoid = clf_sigmoid.predict_proba(X_test)[:, 1]

print("Brier score losses: (the smaller the better)")

clf_score = brier_score_loss(y_test, prob_pos_clf, sample_weight=sw_test)
print("No calibration: %1.3f" % clf_score)

clf_isotonic_score = brier_score_loss(
    y_test, prob_pos_isotonic, sample_weight=sw_test)
print("With isotonic calibration: %1.3f" % clf_isotonic_score)

clf_sigmoid_score = brier_score_loss(
    y_test, prob_pos_sigmoid, sample_weight=sw_test)
print("With sigmoid calibration: %1.3f" % clf_sigmoid_score)

Brier score losses: (the smaller the better)
No calibration: 0.104
With isotonic calibration: 0.084
With sigmoid calibration: 0.109

رسم البيانات والاحتمالات المتوقعة#

plt.figure()
y_unique = np.unique(y)
colors = cm.rainbow(np.linspace(0.0, 1.0, y_unique.size))
for this_y, color in zip(y_unique, colors):
    this_X = X_train[y_train == this_y]
    this_sw = sw_train[y_train == this_y]
    plt.scatter(
        this_X[:, 0],
        this_X[:, 1],
        s=this_sw * 50,
        c=color[np.newaxis, :],
        alpha=0.5,
        edgecolor="k",
        label="Class %s" % this_y,
    )
plt.legend(loc="best")
plt.title("Data")

plt.figure()

order = np.lexsort((prob_pos_clf,))
plt.plot(prob_pos_clf[order], "r", label="No calibration (%1.3f)" % clf_score)
plt.plot(
    prob_pos_isotonic[order],
    "g",
    linewidth=3,
    label="Isotonic calibration (%1.3f)" % clf_isotonic_score,
)
plt.plot(
    prob_pos_sigmoid[order],
    "b",
    linewidth=3,
    label="Sigmoid calibration (%1.3f)" % clf_sigmoid_score,
)
plt.plot(
    np.linspace(0, y_test.size, 51)[1::2],
    y_test[order].reshape(25, -1).mean(1),
    "k",
    linewidth=3,
    label=r"Empirical",
)
plt.ylim([-0.05, 1.05])
plt.xlabel("Instances sorted according to predicted probability (uncalibrated GNB)")
plt.ylabel("P(y=1)")
plt.legend(loc="upper left")
plt.title("Gaussian naive Bayes probabilities")

plt.show()