ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
الحد من الأبعاد باستخدام تحليل مكونات الجوار#
مثال على استخدام تحليل مكونات الجوار للحد من الأبعاد.
يقارن هذا المثال بين طرق مختلفة للحد من الأبعاد (الخطية) تطبق على مجموعة بيانات الأرقام. تحتوي مجموعة البيانات هذه على صور للأرقام من 0 إلى 9 مع حوالي 180 عينة من كل فئة. كل صورة لها أبعاد 8x8 = 64، ويتم تقليلها إلى نقطة بيانات ثنائية الأبعاد.
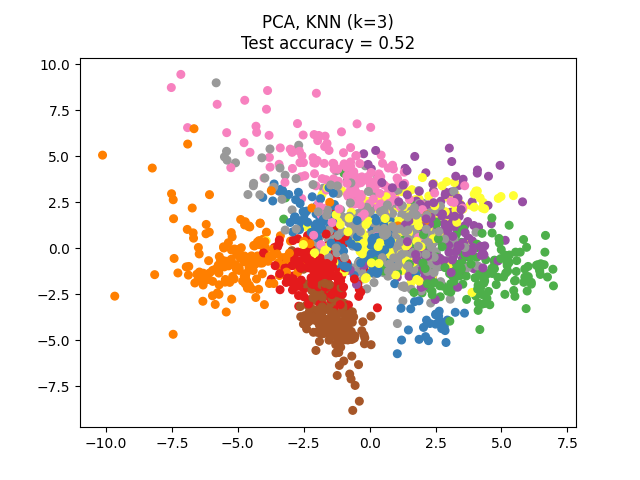
يحدد تحليل المكونات الرئيسية (PCA) المطبق على هذه البيانات مجموعة من السمات (المكونات الرئيسية، أو الاتجاهات في فضاء الميزات) التي تحسب معظم التباين في البيانات. هنا نرسم العينات المختلفة على أول مكونين رئيسيين.
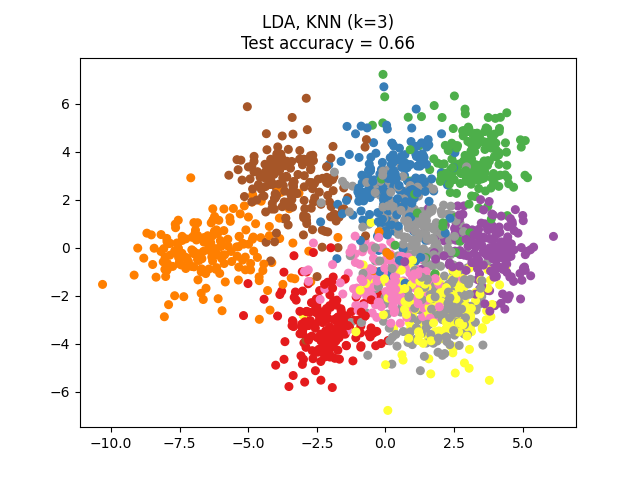
يحاول تحليل التمييز الخطي (LDA) تحديد السمات التي تحسب معظم التباين بين الفئات. على وجه الخصوص، LDA، على عكس PCA، هي طريقة مشرفة، تستخدم تسميات الفئات المعروفة.
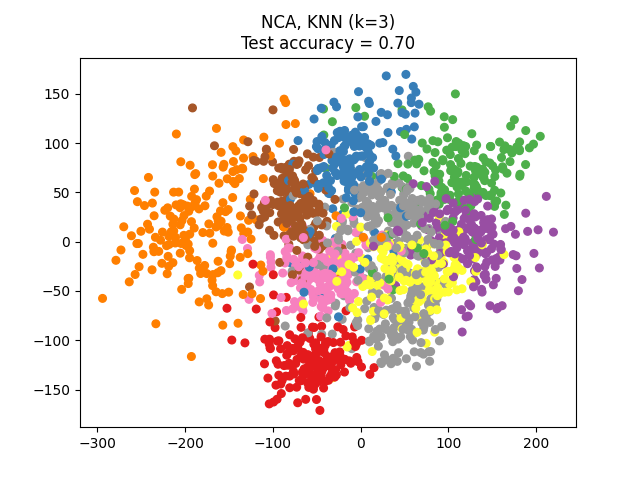
يحاول تحليل مكونات الجوار (NCA) إيجاد فضاء ميزات بحيث يعطي خوارزمية أقرب جار احتمالية أفضل دقة. مثل LDA، إنها طريقة مشرفة.
يمكن للمرء أن يرى أن NCA يفرض تجميعًا للبيانات له معنى بصريًا على الرغم من التخفيض الكبير في البعد.
# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier, NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
n_neighbors = 3
random_state = 0
# تحميل مجموعة بيانات الأرقام
X, y = datasets.load_digits(return_X_y=True)
# تقسيم البيانات إلى مجموعتين تدريب واختبار
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, stratify=y, random_state=random_state
)
dim = len(X[0])
n_classes = len(np.unique(y))
# تقليل البعد إلى 2 باستخدام PCA
pca = make_pipeline(StandardScaler(), PCA(n_components=2, random_state=random_state))
# تقليل البعد إلى 2 باستخدام LinearDiscriminantAnalysis
lda = make_pipeline(StandardScaler(), LinearDiscriminantAnalysis(n_components=2))
# تقليل البعد إلى 2 باستخدام NeighborhoodComponentAnalysis
nca = make_pipeline(
StandardScaler(),
NeighborhoodComponentsAnalysis(n_components=2, random_state=random_state),
)
# استخدام مصنف أقرب جار لتقييم الطرق
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
# إنشاء قائمة بالطرق التي سيتم مقارنتها
dim_reduction_methods = [("PCA", pca), ("LDA", lda), ("NCA", nca)]
# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
plt.figure()
# plt.subplot(1, 3, i + 1, aspect=1)
# ملاءمة نموذج الطريقة
model.fit(X_train, y_train)
# ملاءمة مصنف أقرب جار على مجموعة التدريب المضمنة
knn.fit(model.transform(X_train), y_train)
# حساب دقة أقرب جار على مجموعة الاختبار المضمنة
acc_knn = knn.score(model.transform(X_test), y_test)
# تضمين مجموعة البيانات في بعدين باستخدام النموذج الملائم
X_embedded = model.transform(X)
# رسم النقاط المضمنة وإظهار درجة التقييم
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap="Set1")
plt.title(
"{}, KNN (k={})\nTest accuracy = {:.2f}".format(name, n_neighbors, acc_knn)
)
plt.show()
Total running time of the script: (0 minutes 2.698 seconds)
Related examples
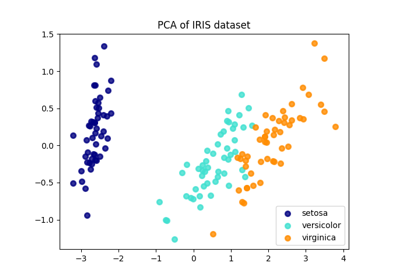
مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA

تعلم متعدد الشعب على الأرقام المكتوبة بخط اليد: التضمين الخطي المحلي، Isomap...
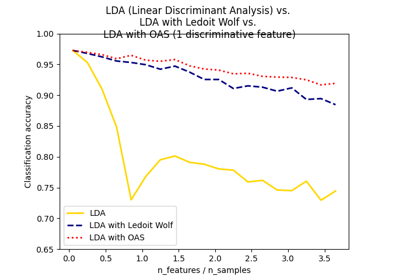
Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification