ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
معايرة الاحتمالات لتصنيف ثلاثي الفئات#
يوضح هذا المثال كيف أن معايرة سيجمويد calibration تغير الاحتمالات المتوقعة لمشكلة تصنيف ثلاثي الفئات. يتم توضيح المضلع الثنائي القياسي، حيث تتوافق الزوايا الثلاثة مع الفئات الثلاث. تشير الأسهم من متجهات الاحتمالات المتوقعة بواسطة مصنف غير معاير إلى متجهات الاحتمالات المتوقعة بواسطة نفس المصنف بعد معايرة سيجمويد على مجموعة بيانات التحقق. تشير الألوان إلى الفئة الحقيقية للعينة (الأحمر: الفئة 1، الأخضر: الفئة 2، الأزرق: الفئة 3).
البيانات#
أدناه، نقوم بإنشاء مجموعة بيانات تصنيف مع 2000 عينة، ميزتين و3 فئات مستهدفة. ثم نقوم بتقسيم البيانات على النحو التالي:
train: 600 عينة (لتدريب المصنف)
valid: 400 عينة (لمعايرة الاحتمالات المتوقعة)
test: 1000 عينة
لاحظ أننا نقوم أيضًا بإنشاء X_train_valid و y_train_valid، والتي تتكون
من كل من مجموعات البيانات الفرعية للتدريب والتحقق. يتم استخدام هذا عندما نريد فقط تدريب
المصنف ولكن لا نريد معايرة الاحتمالات المتوقعة.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
from sklearn.metrics import log_loss
import matplotlib.pyplot as plt
from sklearn.calibration import CalibratedClassifierCV
from sklearn.ensemble import RandomForestClassifier
import numpy as np
from sklearn.datasets import make_blobs
np.random.seed(0)
X, y = make_blobs(
n_samples=2000, n_features=2, centers=3, random_state=42, cluster_std=5.0
)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:1000], y[600:1000]
X_train_valid, y_train_valid = X[:1000], y[:1000]
X_test, y_test = X[1000:], y[1000:]
الملاءمة والمعايرة#
أولاً، سنقوم بتدريب RandomForestClassifier
مع 25 مصنفات أساسية (أشجار) على بيانات التدريب والتحقق
المدمجة (1000 عينة). هذا هو المصنف غير المعاير.
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
لتدريب المصنف المعاير، نبدأ بنفس
RandomForestClassifier ولكن نقوم بتدريبه باستخدام فقط
مجموعة البيانات الفرعية للتدريب (600 عينة) ثم المعايرة، مع method='sigmoid'،
باستخدام مجموعة البيانات الفرعية للتحقق (400 عينة) في عملية من مرحلتين.
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
cal_clf = CalibratedClassifierCV(clf, method="sigmoid", cv="prefit")
cal_clf.fit(X_valid, y_valid)
مقارنة الاحتمالات#
أدناه نرسم مضلع ثنائي مع أسهم توضح التغيير في الاحتمالات المتوقعة لعينات الاختبار.
plt.figure(figsize=(10, 10))
colors = ["r", "g", "b"]
clf_probs = clf.predict_proba(X_test)
cal_clf_probs = cal_clf.predict_proba(X_test)
# رسم الأسهم
for i in range(clf_probs.shape[0]):
plt.arrow(
clf_probs[i, 0],
clf_probs[i, 1],
cal_clf_probs[i, 0] - clf_probs[i, 0],
cal_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]],
head_width=1e-2,
)
# رسم التوقعات المثالية، عند كل زاوية
plt.plot([1.0], [0.0], "ro", ms=20, label="Class 1")
plt.plot([0.0], [1.0], "go", ms=20, label="Class 2")
plt.plot([0.0], [0.0], "bo", ms=20, label="Class 3")
# رسم حدود المضلع الثنائي
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
# إضافة تعليقات توضيحية للنقاط 6 نقاط حول المضلع الثنائي، ونقطة المنتصف داخل المضلع الثنائي
plt.annotate(
r"($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)",
xy=(1.0 / 3, 1.0 / 3),
xytext=(1.0 / 3, 0.23),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.plot([1.0 / 3], [1.0 / 3], "ko", ms=5)
plt.annotate(
r"($\frac{1}{2}$, $0$, $\frac{1}{2}$)",
xy=(0.5, 0.0),
xytext=(0.5, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $\frac{1}{2}$, $\frac{1}{2}$)",
xy=(0.0, 0.5),
xytext=(0.1, 0.5),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($\frac{1}{2}$, $\frac{1}{2}$, $0$)",
xy=(0.5, 0.5),
xytext=(0.6, 0.6),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $0$, $1$)",
xy=(0, 0),
xytext=(0.1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($1$, $0$, $0$)",
xy=(1, 0),
xytext=(1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $1$, $0$)",
xy=(0, 1),
xytext=(0.1, 1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
# إضافة شبكة
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title(
"Change of predicted probabilities on test samples after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
_ = plt.legend(loc="best")
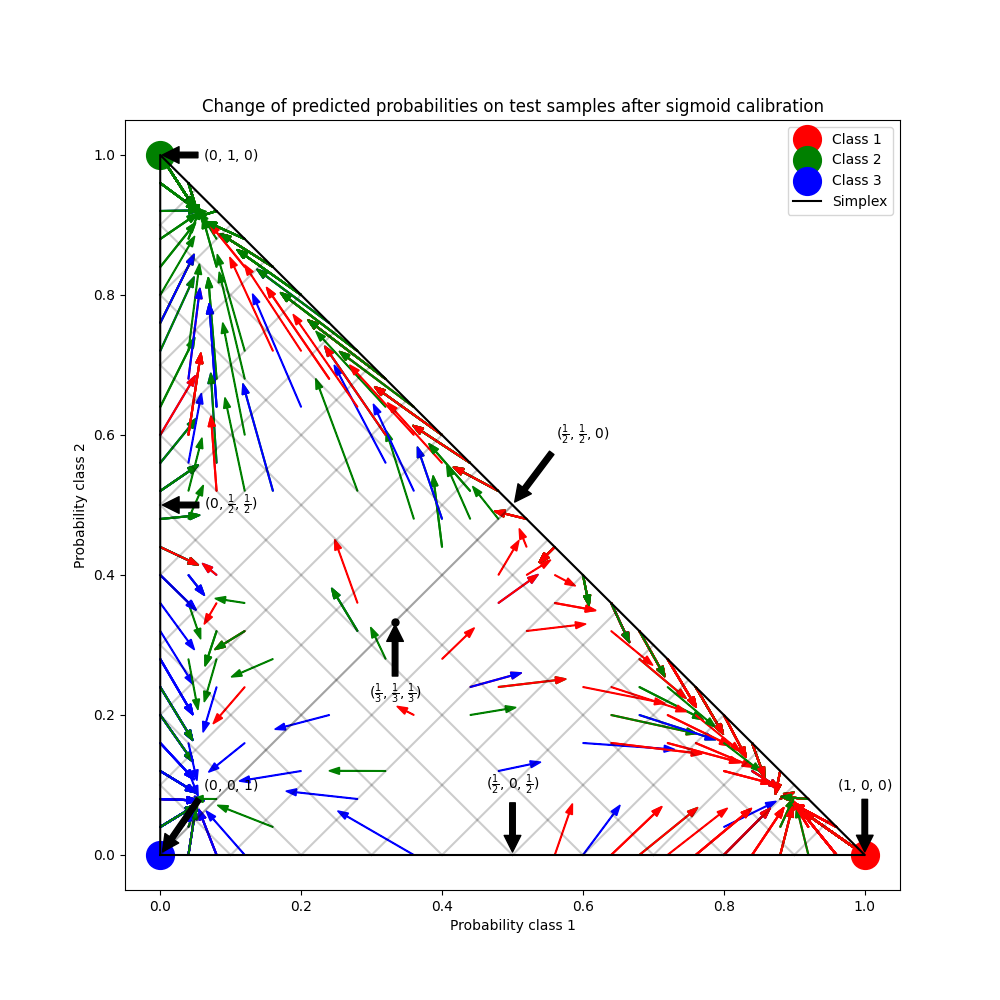
في الشكل أعلاه، تمثل كل زاوية من زوايا المضلع الثنائي فئة متوقعة بشكل مثالي (على سبيل المثال، 1، 0، 0). نقطة المنتصف داخل المضلع الثنائي تمثل توقع الفئات الثلاث باحتمالية متساوية (أي، 1/3، 1/3، 1/3). يبدأ كل سهم من الاحتمالات غير المعايرة وينتهي برأس السهم عند الاحتمالية المعايرة. يمثل لون السهم الفئة الحقيقية لتلك العينة الاختبار.
المصنف غير المعاير مفرط الثقة في تنبؤاته ويتكبد log loss كبير. يتكبد المصنف المعاير log loss أقل بسبب عاملين. أولاً، لاحظ في الشكل أعلاه أن الأسهم تشير بشكل عام بعيدًا عن حواف المضلع الثنائي، حيث احتمال فئة واحدة هو 0. ثانيًا، نسبة كبيرة من الأسهم تشير إلى الفئة الحقيقية، على سبيل المثال، الأسهم الخضراء (العينات التي الفئة الحقيقية هي 'green') تشير بشكل عام إلى الزاوية الخضراء. يؤدي هذا إلى تنبؤات أقل ثقة، 0 احتمالية متوقعة وفي نفس الوقت زيادة في الاحتمالات المتوقعة للفئة الصحيحة. وبالتالي، ينتج المصنف المعاير احتمالات متوقعة أكثر دقة التي تتكبد log loss أقل
يمكننا إظهار هذا بشكل موضوعي من خلال مقارنة log loss
للمصنف غير المعاير والمعاير على تنبؤات 1000
عينات الاختبار. لاحظ أن البديل كان سيكون زيادة عدد
المصنفات الأساسية (الأشجار) لـ
RandomForestClassifier والتي كانت ستؤدي
إلى انخفاض مماثل في log loss.
Log-loss of
* uncalibrated classifier: 1.327
* calibrated classifier: 0.549
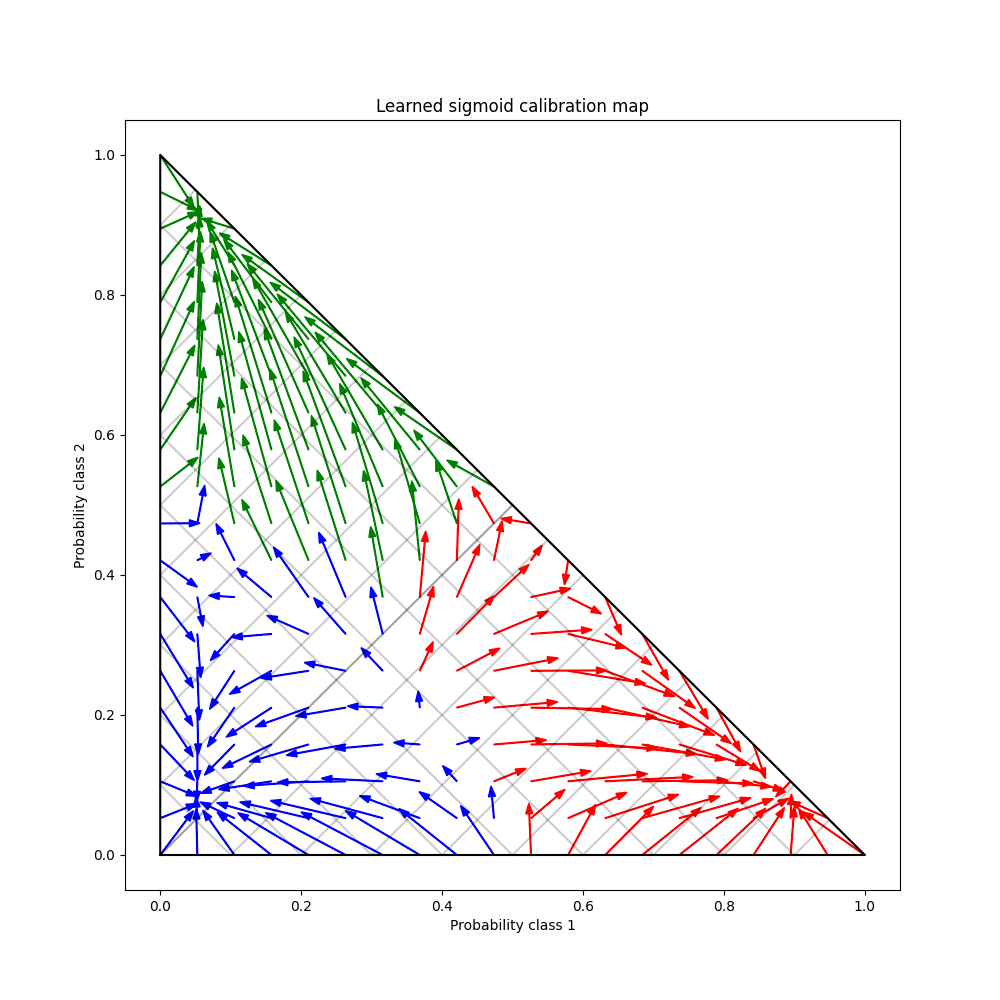
أخيرًا نقوم بإنشاء شبكة من الاحتمالات غير المعايرة المحتملة عبر المضلع الثنائي، ونحسب الاحتمالات المعايرة ونرسم أسهم لكل منها. يتم تلوين الأسهم وفقًا لأعلى الاحتمالية غير المعايرة. يوضح هذا خريطة المعايرة التي تم تعلمها:
plt.figure(figsize=(10, 10))
# إنشاء شبكة من قيم الاحتمالية
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
# استخدام المصنفات الثلاثة لمعايرة الفئات لحساب الاحتمالات المعايرة
calibrated_classifier = cal_clf.calibrated_classifiers_[0]
prediction = np.vstack(
[
calibrator.predict(this_p)
for calibrator, this_p in zip(calibrated_classifier.calibrators, p.T)
]
).T
# إعادة تطبيع التنبؤات المعايرة للتأكد من أنها تبقى داخل
# المضلع الثنائي. تتم نفس خطوة إعادة التطبيع داخليًا بواسطة
# طريقة التنبؤ لـ CalibratedClassifierCV على مشاكل متعددة الفئات.
prediction /= prediction.sum(axis=1)[:, None]
# رسم التغييرات في الاحتمالات المتوقعة التي تسببها المصنفات المعايرة
for i in range(prediction.shape[0]):
plt.arrow(
p[i, 0],
p[i, 1],
prediction[i, 0] - p[i, 0],
prediction[i, 1] - p[i, 1],
head_width=1e-2,
color=colors[np.argmax(p[i])],
)
# رسم حدود المضلع الثنائي
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Learned sigmoid calibration map")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
Total running time of the script: (0 minutes 1.806 seconds)
Related examples