ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
المتجه الذاتي الرئيسي لويكيبيديا#
هناك طريقة كلاسيكية لتأكيد الأهمية النسبية للرؤوس في الرسم البياني هو حساب المتجه الذاتي الرئيسي لمصفوفة المجاورة حتى يتم تعيين قيم مكونات المتجه الذاتي الأول لكل رأس كدرجة مركزية: https://en.wikipedia.org/wiki/Eigenvector_centrality. على رسم بياني للصفحات والروابط تسمى هذه القيم بتصنيفات PageRank من قبل Google.
هدف هذا المثال هو تحليل الرسم البياني للروابط داخل مقالات ويكيبيديا لتصنيف المقالات حسب الأهمية النسبية وفقا لهذه المركزية المتجهة الذاتية.
الطريقة التقليدية لحساب المتجه الذاتي الرئيسي هي استخدام طريقة تكرار القوة. هنا يتم إنجاز الحساب بفضل خوارزمية SVD العشوائية لمارتينسون المطبقة في scikit-learn.
يتم جلب بيانات الرسم البياني من إغراق DBpedia. DBpedia هي استخراج لبيانات ويكيبيديا الهيكلية الكامنة.
Download data, if not already on disk#
redirects_url = "http://downloads.dbpedia.org/3.5.1/en/redirects_en.nt.bz2"
redirects_filename = redirects_url.rsplit("/", 1)[1]
page_links_url = "http://downloads.dbpedia.org/3.5.1/en/page_links_en.nt.bz2"
page_links_filename = page_links_url.rsplit("/", 1)[1]
resources = [
(redirects_url, redirects_filename),
(page_links_url, page_links_filename),
]
for url, filename in resources:
if not os.path.exists(filename):
print("Downloading data from '%s', please wait..." % url)
opener = urlopen(url)
with open(filename, "wb") as f:
f.write(opener.read())
print()
تحميل ملفات إعادة التوجيه#
def index(redirects, index_map, k):
"""Find the index of an article name after redirect resolution"""
k = redirects.get(k, k)
return index_map.setdefault(k, len(index_map))
DBPEDIA_RESOURCE_PREFIX_LEN = len("http://dbpedia.org/resource/")
SHORTNAME_SLICE = slice(DBPEDIA_RESOURCE_PREFIX_LEN + 1, -1)
def short_name(nt_uri):
"""Remove the < and > URI markers and the common URI prefix"""
return nt_uri[SHORTNAME_SLICE]
def get_redirects(redirects_filename):
"""Parse the redirections and build a transitively closed map out of it"""
redirects = {}
print("Parsing the NT redirect file")
for l, line in enumerate(BZ2File(redirects_filename)):
split = line.split()
if len(split) != 4:
print("ignoring malformed line: " + line)
continue
redirects[short_name(split[0])] = short_name(split[2])
if l % 1000000 == 0:
print("[%s] line: %08d" % (datetime.now().isoformat(), l))
# compute the transitive closure
print("Computing the transitive closure of the redirect relation")
for l, source in enumerate(redirects.keys()):
transitive_target = None
target = redirects[source]
seen = {source}
while True:
transitive_target = target
target = redirects.get(target)
if target is None or target in seen:
break
seen.add(target)
redirects[source] = transitive_target
if l % 1000000 == 0:
print("[%s] line: %08d" % (datetime.now().isoformat(), l))
return redirects
حساب مصفوفة المجاورة#
def get_adjacency_matrix(redirects_filename, page_links_filename, limit=None):
"""Extract the adjacency graph as a scipy sparse matrix
Redirects are resolved first.
Redirects are resolved first.
Returns X, the scipy sparse adjacency matrix, redirects as python
dict from article names to article names and index_map a python dict
from article names to python int (article indexes).
"""
print("Computing the redirect map")
redirects = get_redirects(redirects_filename)
print("Computing the integer index map")
index_map = dict()
links = list()
for l, line in enumerate(BZ2File(page_links_filename)):
split = line.split()
if len(split) != 4:
print("ignoring malformed line: " + line)
continue
i = index(redirects, index_map, short_name(split[0]))
j = index(redirects, index_map, short_name(split[2]))
links.append((i, j))
if l % 1000000 == 0:
print("[%s] line: %08d" % (datetime.now().isoformat(), l))
if limit is not None and l >= limit - 1:
break
print("Computing the adjacency matrix")
X = sparse.lil_matrix((len(index_map), len(index_map)), dtype=np.float32)
for i, j in links:
X[i, j] = 1.0
del links
print("Converting to CSR representation")
X = X.tocsr()
print("CSR conversion done")
return X, redirects, index_map
# التوقف بعد 5M من الروابط لجعل العمل ممكنا في RAM
X, redirects, index_map = get_adjacency_matrix(
redirects_filename, page_links_filename, limit=5000000
)
names = {i: name for name, i in index_map.items()}
حساب المتجه المنفرد الرئيسي باستخدام SVD العشوائية#
print("Computing the principal singular vectors using randomized_svd")
t0 = time()
U, s, V = randomized_svd(X, 5, n_iter=3)
print("done in %0.3fs" % (time() - t0))
# طباعة أسماء أقوى مكونات ويكيبيديا ذات الصلة للمتجه المنفرد الرئيسي
# والتي يجب أن تكون مشابهة لأعلى متجه ذاتي
print("Top wikipedia pages according to principal singular vectors")
pprint([names[i] for i in np.abs(U.T[0]).argsort()[-10:]])
pprint([names[i] for i in np.abs(V[0]).argsort()[-10:]])
حساب درجات المركزية#
def centrality_scores(X, alpha=0.85, max_iter=100, tol=1e-10):
"""Power iteration computation of the principal eigenvector
This method is also known as Google PageRank and the implementation
is based on the one from the NetworkX project (BSD licensed too)
with copyrights by:
Aric Hagberg <hagberg@lanl.gov>
Dan Schult <dschult@colgate.edu>
Pieter Swart <swart@lanl.gov>
"""
n = X.shape[0]
X = X.copy()
incoming_counts = np.asarray(X.sum(axis=1)).ravel()
print("Normalizing the graph")
for i in incoming_counts.nonzero()[0]:
X.data[X.indptr[i] : X.indptr[i + 1]] *= 1.0 / incoming_counts[i]
dangle = np.asarray(np.where(np.isclose(X.sum(axis=1), 0), 1.0 / n, 0)).ravel()
scores = np.full(n, 1.0 / n, dtype=np.float32) # initial guess
for i in range(max_iter):
print("power iteration #%d" % i)
prev_scores = scores
scores = (
alpha * (scores * X + np.dot(dangle, prev_scores))
+ (1 - alpha) * prev_scores.sum() / n
)
# check convergence: normalized l_inf norm
scores_max = np.abs(scores).max()
if scores_max == 0.0:
scores_max = 1.0
err = np.abs(scores - prev_scores).max() / scores_max
print("error: %0.6f" % err)
if err < n * tol:
return scores
return scores
print("Computing principal eigenvector score using a power iteration method")
t0 = time()
scores = centrality_scores(X, max_iter=100)
print("done in %0.3fs" % (time() - t0))
pprint([names[i] for i in np.abs(scores).argsort()[-10:]])
Related examples
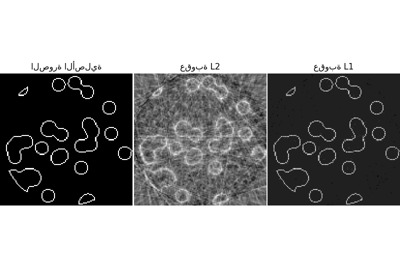
sphx_glr_auto_examples_applications_plot_tomography_l1_reconstruction.py
هذا مثال يوضح إعادة بناء صورة من مجموعة من الإسقاطات المتوازية، والتي تم الحصول عليها على طول زوايا مختلفة. يتم الحصول على مثل هذه البيانات في التصوير المقطعي المحوسب (CT).
التجميع الثنائي للمستندات باستخدام خوارزمية التجميع الطيفي المشترك
التجميع الثنائي للمستندات باستخدام خوارزمية التجميع الطيفي المشترك
