ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
رسم منحنيات التعلم وفحص قابلية التوسع للنماذج#
في هذا المثال، نُظهر كيفية استخدام الفئة
LearningCurveDisplay لرسم منحنيات التعلم بسهولة. بالإضافة إلى ذلك، نقدم تفسيرًا لمنحنيات التعلم التي تم الحصول عليها
لمصنفي خوارزمية بايز الساذجة والآلة الداعمة للمتجهات (SVM).
بعد ذلك، نستكشف بعض الاستنتاجات حول قابلية التوسع لهذه النماذج التنبؤية من خلال النظر في تكلفتها الحسابية وليس فقط في دقتها الإحصائية.
# المؤلفون: مطوري مكتبة ساي كيت ليرن
# معرف رخصة إس بي دي إكس: BSD-3-Clause
منحنى التعلم#
توضح منحنيات التعلم تأثير إضافة المزيد من العينات أثناء عملية التدريب. يتم تصوير هذا التأثير من خلال فحص الأداء الإحصائي للنموذج من حيث درجة التدريب ودرجة الاختبار.
هنا، نحسب منحنى التعلم لمصنف خوارزمية بايز الساذجة ومصنف الآلة الداعمة للمتجهات (SVM) باستخدام نواة RBF ومجموعة بيانات الأرقام.
from sklearn.datasets import load_digits
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
X, y = load_digits(return_X_y=True)
naive_bayes = GaussianNB()
svc = SVC(kernel="rbf", gamma=0.001)
الطريقة from_estimator
تعرض منحنى التعلم بالنظر إلى مجموعة البيانات والنموذج التنبؤي المراد تحليله. للحصول على تقدير لعدم اليقين في الدرجات، تستخدم هذه الطريقة
إجراء التقسيم المتقاطع.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import LearningCurveDisplay, ShuffleSplit
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 6), sharey=True)
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"score_type": "both",
"n_jobs": 4,
"line_kw": {"marker": "o"},
"std_display_style": "fill_between",
"score_name": "Accuracy",
}
for ax_idx, estimator in enumerate([naive_bayes, svc]):
LearningCurveDisplay.from_estimator(estimator, **common_params, ax=ax[ax_idx])
handles, label = ax[ax_idx].get_legend_handles_labels()
ax[ax_idx].legend(handles[:2], ["Training Score", "Test Score"])
ax[ax_idx].set_title(f"Learning Curve for {estimator.__class__.__name__}")
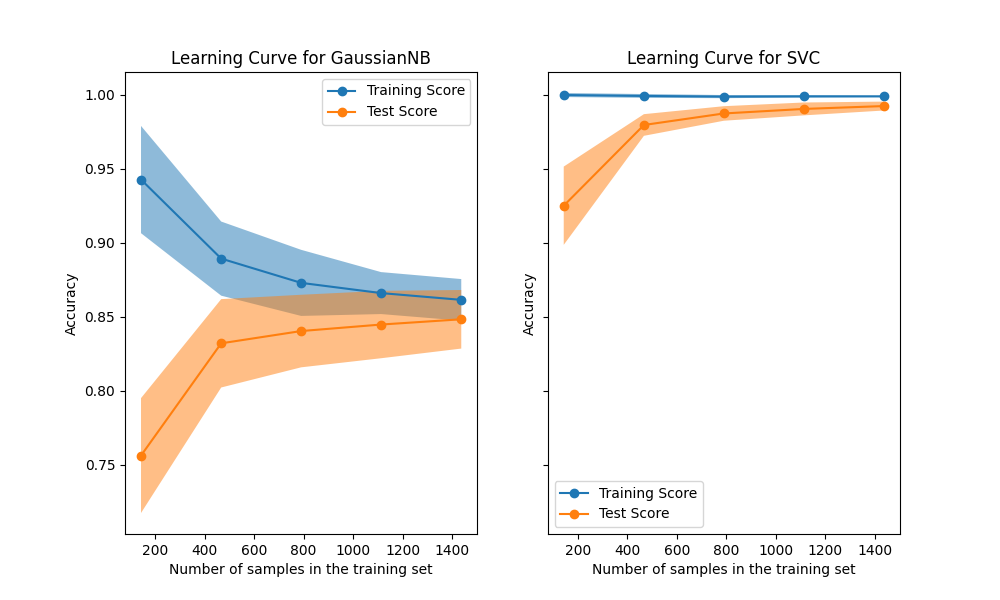
نحلل أولاً منحنى التعلم لمصنف خوارزمية بايز الساذجة. يمكن العثور على شكله في مجموعات البيانات الأكثر تعقيدًا في كثير من الأحيان: تكون درجة التدريب عالية جدًا عند استخدام عدد قليل من العينات للتدريب وتنخفض عند زيادة عدد العينات، في حين تكون درجة الاختبار منخفضة جدًا في البداية ثم تزيد عند إضافة العينات. تصبح درجات التدريب والاختبار أكثر واقعية عند استخدام جميع العينات للتدريب.
نرى منحنى تعلم آخر نموذجي لمصنف الآلة الداعمة للمتجهات (SVM) مع نواة RBF. تظل درجة التدريب مرتفعة بغض النظر عن حجم مجموعة التدريب. من ناحية أخرى، تزيد درجة الاختبار مع حجم مجموعة التدريب. في الواقع، تزيد حتى تصل إلى نقطة تصل فيها إلى مستوى ثابت. ملاحظة مثل هذا المستوى الثابت هي إشارة إلى أنه قد لا يكون من المفيد الحصول على بيانات جديدة لتدريب النموذج حيث أن أداء تعميم النموذج لن يزيد بعد الآن.
تحليل التعقيد#
بالإضافة إلى منحنيات التعلم هذه، من الممكن أيضًا النظر إلى قابلية التوسع للنماذج التنبؤية من حيث أوقات التدريب والتصنيف.
الفئة LearningCurveDisplay لا
توفر مثل هذه المعلومات. نحتاج إلى اللجوء إلى
الدالة learning_curve بدلاً من ذلك وإنشاء
الرسم يدويًا.
from sklearn.model_selection import learning_curve
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"n_jobs": 4,
"return_times": True,
}
train_sizes, _, test_scores_nb, fit_times_nb, score_times_nb = learning_curve(
naive_bayes, **common_params
)
train_sizes, _, test_scores_svm, fit_times_svm, score_times_svm = learning_curve(
svc, **common_params
)
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(16, 12), sharex=True)
for ax_idx, (fit_times, score_times, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[score_times_nb, score_times_svm],
[naive_bayes, svc],
)
):
# قابلية التوسع فيما يتعلق بوقت التلاؤم
ax[0, ax_idx].plot(train_sizes, fit_times.mean(axis=1), "o-")
ax[0, ax_idx].fill_between(
train_sizes,
fit_times.mean(axis=1) - fit_times.std(axis=1),
fit_times.mean(axis=1) + fit_times.std(axis=1),
alpha=0.3,
)
ax[0, ax_idx].set_ylabel("Fit time (s)")
ax[0, ax_idx].set_title(
f"Scalability of the {estimator.__class__.__name__} classifier"
)
# قابلية التوسع فيما يتعلق بوقت التصنيف
ax[1, ax_idx].plot(train_sizes, score_times.mean(axis=1), "o-")
ax[1, ax_idx].fill_between(
train_sizes,
score_times.mean(axis=1) - score_times.std(axis=1),
score_times.mean(axis=1) + score_times.std(axis=1),
alpha=0.3,
)
ax[1, ax_idx].set_ylabel("Score time (s)")
ax[1, ax_idx].set_xlabel("Number of training samples")
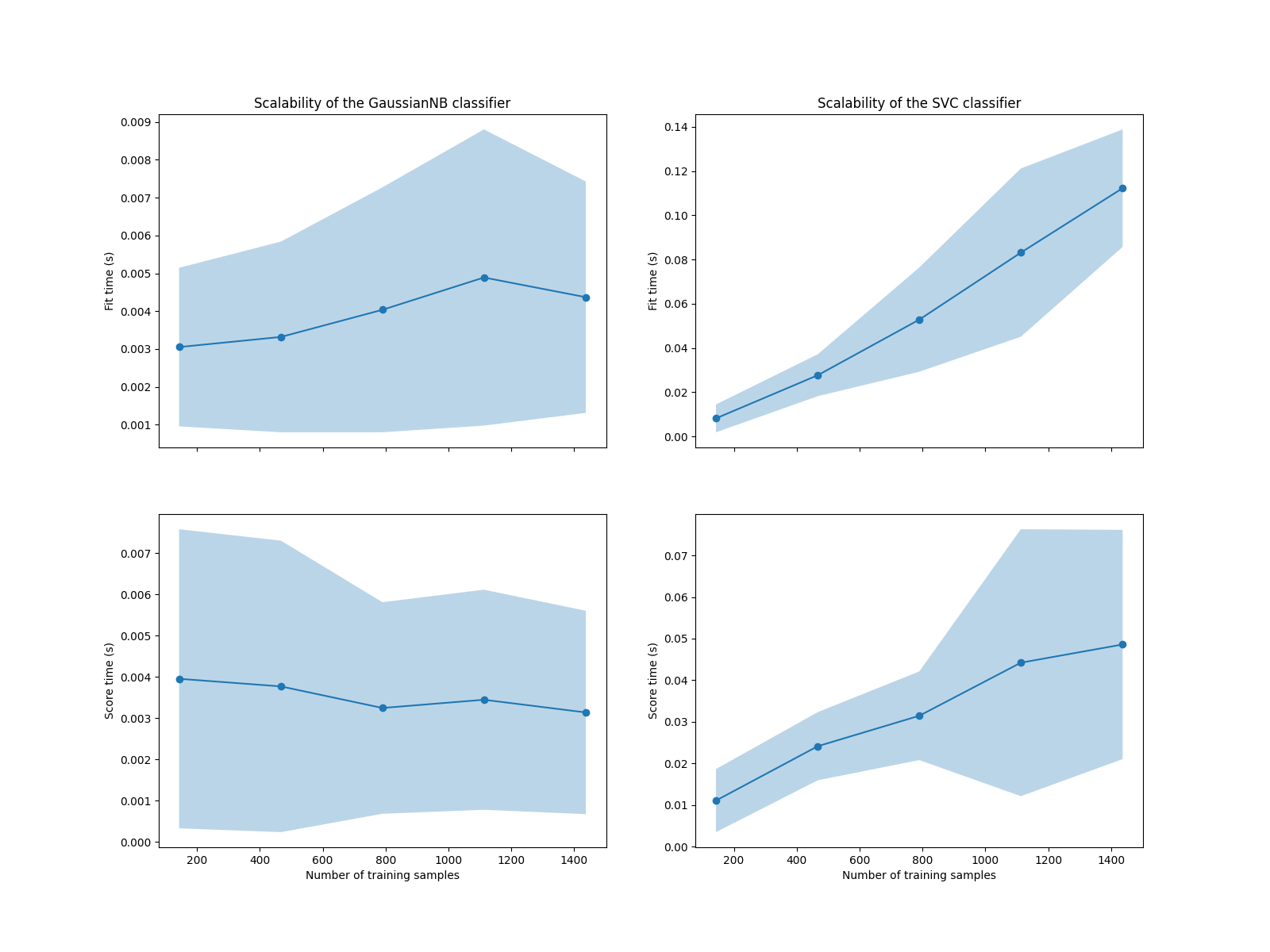
نرى أن قابلية التوسع لمصنفي الآلة الداعمة للمتجهات (SVM) وخوارزمية بايز الساذجة مختلفة جدًا. تزداد تعقيد مصنف الآلة الداعمة للمتجهات (SVM) بسرعة كبيرة مع عدد العينات. في الواقع، من المعروف أن تعقيد وقت التلاؤم لهذا المصنف أكثر من تربيعي مع عدد العينات مما يجعله من الصعب توسيع نطاقه ليشمل مجموعة بيانات تحتوي على أكثر من بضعة 10,000 عينة. على النقيض من ذلك، يتوسع مصنف خوارزمية بايز الساذجة بشكل أفضل بكثير مع تعقيد أقل في وقت التلاؤم والتصنيف.
بعد ذلك، يمكننا التحقق من التوازن بين زيادة وقت التدريب ودرجة التقسيم المتقاطع.
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(16, 6))
for ax_idx, (fit_times, test_scores, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[test_scores_nb, test_scores_svm],
[naive_bayes, svc],
)
):
ax[ax_idx].plot(fit_times.mean(axis=1), test_scores.mean(axis=1), "o-")
ax[ax_idx].fill_between(
fit_times.mean(axis=1),
test_scores.mean(axis=1) - test_scores.std(axis=1),
test_scores.mean(axis=1) + test_scores.std(axis=1),
alpha=0.3,
)
ax[ax_idx].set_ylabel("Accuracy")
ax[ax_idx].set_xlabel("Fit time (s)")
ax[ax_idx].set_title(
f"Performance of the {estimator.__class__.__name__} classifier"
)
plt.show()
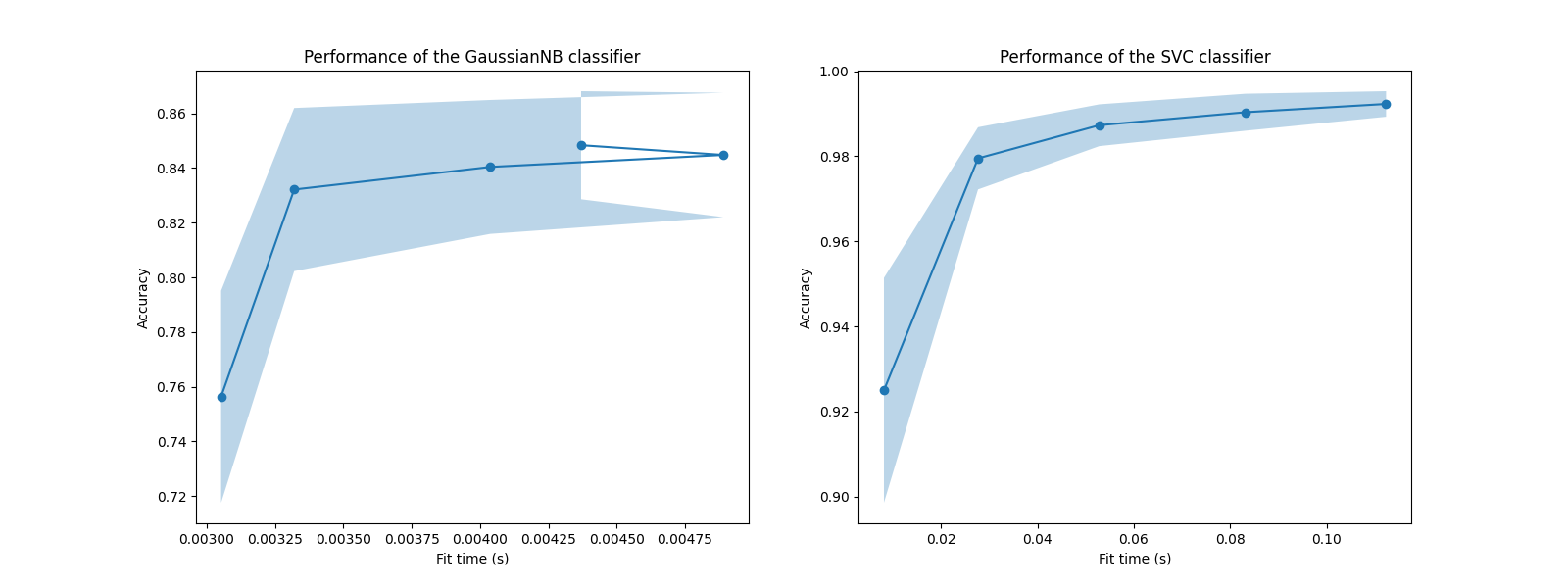
في هذه الرسوم البيانية، يمكننا البحث عن نقطة الانعطاف التي لا تزيد فيها درجة التقسيم المتقاطع بعد الآن ويزيد فقط وقت التدريب.
Total running time of the script: (0 minutes 29.060 seconds)
Related examples