مقارنة بين المُقدر الفردي والتجميع: تحليل الانحياز والتشتت

يوضح هذا المثال ويقارن تحليل الانحياز والتشتت للخطأ التربيعي المتوسط المتوقع لمقدر فردي مقابل مجموعة تجميع.

في الانحدار، يمكن تحليل الخطأ التربيعي المتوسط المتوقع لمقدر من حيث الانحياز والتشتت والضوضاء. في المتوسط على مجموعات البيانات لمشكلة الانحدار، يقيس مصطلح الانحياز متوسط الكمية التي تختلف بها تنبؤات المقدر عن تنبؤات أفضل مقدر ممكن للمشكلة (أي نموذج بايز). يقيس مصطلح التشتت تباين تنبؤات المقدر عند التكيف على حالات مختلفة عشوائية من نفس المشكلة. يتم تمييز كل حالة للمشكلة بـ "LS"، والتي تعني "عينة التعلم"، فيما يلي. وأخيراً، تقيس الضوضاء الجزء الذي لا يمكن تخفيضه من الخطأ والذي يرجع إلى التباين في البيانات.

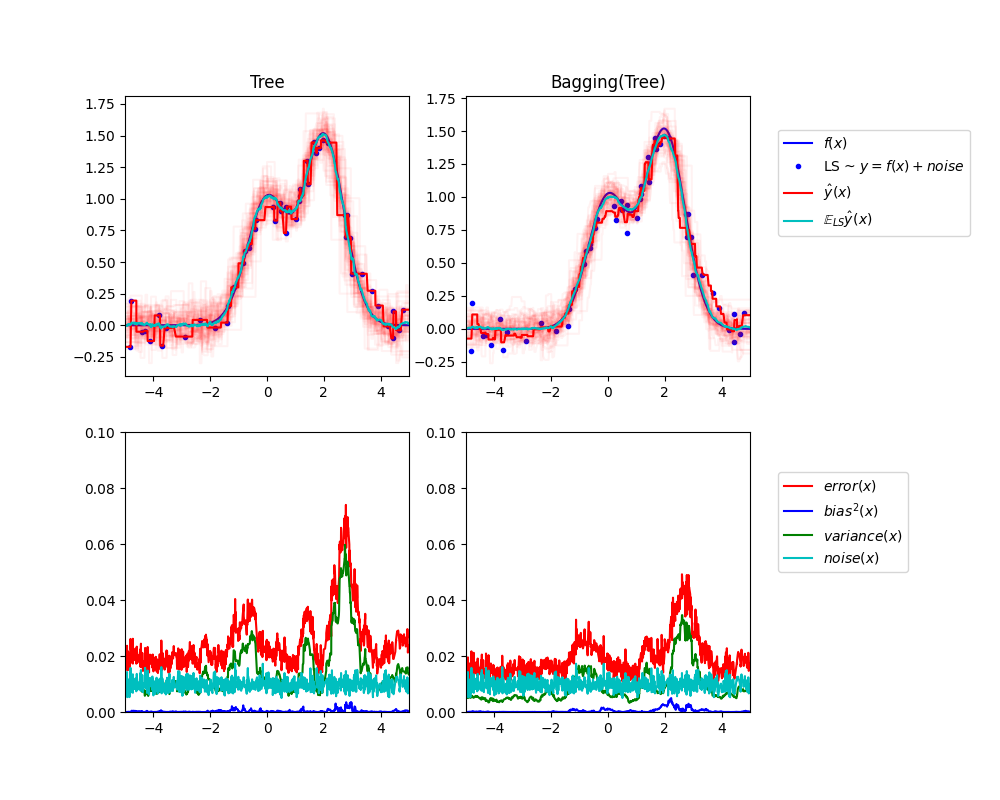
يوضح الشكل العلوي الأيسر تنبؤات (باللون الأحمر الداكن) لشجرة قرار فردية مدربة على مجموعة بيانات عشوائية LS (النقاط الزرقاء) لمشكلة انحدار تجريبية أحادية البعد. كما يوضح تنبؤات (باللون الأحمر الفاتح) لشجرات قرار فردية أخرى مدربة على مجموعات بيانات عشوائية أخرى (ومختلفة) من نفس المشكلة. بديهياً، يتوافق مصطلح التشتت هنا مع عرض حزمة تنبؤات (باللون الأحمر الفاتح) للمقدرات الفردية. كلما زاد التشتت، كلما زادت حساسية التنبؤات لـ "x" للتغيرات الصغيرة في مجموعة التدريب. يتوافق مصطلح الانحياز مع الفرق بين التنبؤ المتوسط للمقدر (باللون السماوي) وأفضل نموذج ممكن (باللون الأزرق الداكن). في هذه المشكلة، يمكننا أن نلاحظ أن الانحياز منخفض جدًا (كل من المنحنيات السماوية والزرقاء قريبة من بعضها البعض) في حين أن التشتت كبير (الحزمة الحمراء واسعة إلى حد ما).

يرسم الشكل السفلي الأيسر التحليل النقطي للخطأ التربيعي المتوسط المتوقع لشجرة قرار فردية. يؤكد أن مصطلح الانحياز (باللون الأزرق) منخفض في حين أن التشتت كبير (باللون الأخضر). كما يوضح أيضًا جزء الضوضاء من الخطأ والذي، كما هو متوقع، يبدو ثابتًا وحوالي 0.01.

تتوافق الأشكال اليمنى مع نفس الرسوم البيانية ولكن باستخدام مجموعة تجميع من شجرات القرار بدلاً من ذلك. في كلا الشكلين، يمكننا أن نلاحظ أن مصطلح الانحياز أكبر من الحالة السابقة. في الشكل العلوي الأيمن، الفرق بين التنبؤ المتوسط (باللون السماوي) وأفضل نموذج ممكن أكبر (على سبيل المثال، لاحظ الانزياح حول x=2). في الشكل السفلي الأيمن، منحنى الانحياز أعلى قليلاً أيضًا من الشكل السفلي الأيسر. من حيث التشتت، فإن حزمة التنبؤات أضيق، مما يشير إلى أن التشتت أقل. في الواقع، كما يؤكد الشكل السفلي الأيمن، فإن مصطلح التشتت (باللون الأخضر) أقل من شجرات القرار الفردية. بشكل عام، لم يعد تحليل الانحياز والتشتت هو نفسه. المقايضة أفضل للتجميع: إن حساب المتوسط لعدة شجرات قرار مدربة على نسخ التمهيد من مجموعة البيانات يزيد قليلاً من مصطلح الانحياز ولكنه يسمح بتخفيض أكبر للتشتت، مما يؤدي إلى خطأ تربيعي متوسط أقل بشكل عام (قارن المنحنيات الحمراء في الأشكال السفلية). يؤكد ناتج البرنامج النصي أيضًا على هذه الحدسية. الخطأ الكلي لمجموعة التجميع أقل من الخطأ الكلي لشجرة قرار فردية، وهذا الفرق ينبع في الواقع بشكل أساسي من تشتت أقل.

للحصول على مزيد من التفاصيل حول تحليل الانحياز والتشتت، راجع القسم 7.3 من [1].

مراجع

[1]

T. Hastie, R. Tibshirani and J. Friedman, "Elements of Statistical Learning", Springer, 2009.

Tree: 0.0255 (error) = 0.0003 (bias^2)  + 0.0152 (var) + 0.0098 (noise)
Bagging(Tree): 0.0196 (error) = 0.0004 (bias^2)  + 0.0092 (var) + 0.0098 (noise)

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# الإعدادات
n_repeat = 50  # عدد التكرارات لحساب التوقعات
n_train = 50  # حجم مجموعة التدريب
n_test = 1000  # حجم مجموعة الاختبار
noise = 0.1  # الانحراف المعياري للضوضاء
np.random.seed(0)

# قم بتغيير هذا لاستكشاف تحليل الانحياز والتشتت لمقدرات أخرى. يجب أن يعمل هذا بشكل جيد لمقدرات ذات تشتت عالٍ (مثل شجرات القرار أو KNN)، ولكن بشكل سيء لمقدرات ذات تشتت منخفض (مثل النماذج الخطية).
estimators = [
    ("Tree", DecisionTreeRegressor()),
    ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor())),
]

n_estimators = len(estimators)


# توليد البيانات
def f(x):
    x = x.ravel()

    return np.exp(-(x**2)) + 1.5 * np.exp(-((x - 2) ** 2))


def generate(n_samples, noise, n_repeat=1):
    X = np.random.rand(n_samples) * 10 - 5
    X = np.sort(X)

    if n_repeat == 1:
        y = f(X) + np.random.normal(0.0, noise, n_samples)
    else:
        y = np.zeros((n_samples, n_repeat))

        for i in range(n_repeat):
            y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

    X = X.reshape((n_samples, 1))

    return X, y


X_train = []
y_train = []

for i in range(n_repeat):
    X, y = generate(n_samples=n_train, noise=noise)
    X_train.append(X)
    y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# التكرار على estimators للمقارنة
for n, (name, estimator) in enumerate(estimators):
    # حساب التنبؤات
    y_predict = np.zeros((n_test, n_repeat))

    for i in range(n_repeat):
        estimator.fit(X_train[i], y_train[i])
        y_predict[:, i] = estimator.predict(X_test)

    # تحليل الانحياز^2 + التشتت + الضوضاء للخطأ التربيعي المتوسط
    y_error = np.zeros(n_test)

    for i in range(n_repeat):
        for j in range(n_repeat):
            y_error += (y_test[:, j] - y_predict[:, i]) ** 2

    y_error /= n_repeat * n_repeat

    y_noise = np.var(y_test, axis=1)
    y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
    y_var = np.var(y_predict, axis=1)

    print(
        "{0}: {1:.4f} (error) = {2:.4f} (bias^2) "
        " + {3:.4f} (var) + {4:.4f} (noise)".format(
            name, np.mean(y_error), np.mean(
                y_bias), np.mean(y_var), np.mean(y_noise)
        )
    )

    # رسم الأشكال
    plt.subplot(2, n_estimators, n + 1)
    plt.plot(X_test, f(X_test), "b", label="$f(x)$")
    plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

    for i in range(n_repeat):
        if i == 0:
            plt.plot(X_test, y_predict[:, i], "r", label=r"$\^y(x)$")
        else:
            plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

    plt.plot(X_test, np.mean(y_predict, axis=1),
             "c", label=r"$\mathbb{E}_{LS} \^y(x)$")

    plt.xlim([-5, 5])
    plt.title(name)

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

    plt.subplot(2, n_estimators, n_estimators + n + 1)
    plt.plot(X_test, y_error, "r", label="$error(x)$")
    plt.plot(X_test, y_bias, "b", label="$bias^2(x)$"),
    plt.plot(X_test, y_var, "g", label="$variance(x)$"),
    plt.plot(X_test, y_noise, "c", label="$noise(x)$")

    plt.xlim([-5, 5])
    plt.ylim([0, 0.1])

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

plt.subplots_adjust(right=0.75)
plt.show()

Related examples

sphx_glr_auto_examples_classification_plot_lda_qda.py

هذا مثال لرسم حدود التمييز والقطع الناقص لتشتت كل فئة، والتي تم تعلمها بواسطة LinearDiscriminantAnalysis (LDA) و QuadraticDiscriminantAnalysis (QDA). يُظهر القطع الناقص الانحراف المعياري المزدوج لكل فئة. مع LDA، يكون الانحراف المعياري هو نفسه لجميع الفئات، في حين أن لكل فئة انحرافها المعياري الخاص بها مع QDA.

انحدار شجرة القرار مع AdaBoost

انحدار شجرة القرار مع AdaBoost

فترات التنبؤ لانحدار التعزيز المتدرج

فترات التنبؤ لانحدار التعزيز المتدرج

sphx_glr_auto_examples_linear_model_plot_bayesian_ridge_curvefit.py

# ========================================================