ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
نسب الاحتمال الطبقي لقياس أداء التصنيف#
هذا المثال يوضح الدالة class_likelihood_ratios
والتي تقوم بحساب نسب الاحتمال الطبقي الإيجابية والسلبية (LR+,
LR-) لتقييم القوة التنبؤية لمصنف ثنائي. كما سنرى،
هذه المقاييس مستقلة عن نسبة التوازن بين الفئات في مجموعة الاختبار،
مما يجعلها مفيدة للغاية عندما تختلف نسبة التوازن بين الفئات في البيانات المتاحة للدراسة عن نسبة التوازن في التطبيق المستهدف.
الاستخدام النموذجي هو دراسة الحالة-المراقبة في الطب، والتي لديها توازن تقريبًا بين الفئات بينما يوجد اختلال كبير في التوازن بين الفئات في السكان بشكل عام. في مثل هذه التطبيقات، يمكن اختيار احتمالية ما قبل الاختبار لوجود حالة معينة لدى فرد ما لتكون هي نسبة الانتشار، أي نسبة السكان الذين يعانون من حالة طبية معينة. تمثل احتمالية ما بعد الاختبار عندئذٍ احتمالية وجود الحالة بالفعل نظرًا لنتيجة الاختبار الإيجابية.
في هذا المثال، نناقش أولاً العلاقة بين احتمالية ما قبل الاختبار واحتمالية ما بعد الاختبار والتي تعطى بواسطة نسب احتمالية الفئة. ثم نقيم سلوكها في بعض السيناريوهات الخاضعة للتحكم. في القسم الأخير، نرسمها كدالة لنسبة انتشار الفئة الإيجابية.
# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause
تحليل ما قبل الاختبار مقابل ما بعد الاختبار#
لنفترض أن لدينا مجموعة من السكان مع قياسات فيزيولوجية X
والتي يمكن أن تكون مؤشرات حيوية غير مباشرة للمرض ومؤشرات حقيقية
للمرض y (الحقيقة الأرضية). معظم الناس في السكان لا
يحملون المرض ولكن أقلية (في هذه الحالة حوالي 10٪) تفعل ذلك:
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=10_000, weights=[0.9, 0.1], random_state=0)
print(f"نسبة الأشخاص الذين يحملون المرض: {100*y.mean():.2f}%")
نسبة الأشخاص الذين يحملون المرض: 10.37%
يتم بناء نموذج تعلم آلي لتشخيص ما إذا كان الشخص مع بعض القياسات الفيزيولوجية من المرجح أن يحمل المرض محل الاهتمام. لتقييم النموذج، نحتاج إلى تقييم أدائه على مجموعة اختبار محجوزة:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
بعد ذلك يمكننا ملاءمة نموذج التشخيص لدينا وحساب نسبة الاحتمال الطبقي الإيجابية لتقييم فائدة هذا المصنف كأداة لتشخيص المرض:
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import class_likelihood_ratios
estimator = LogisticRegression().fit(X_train, y_train)
y_pred = estimator.predict(X_test)
pos_LR, neg_LR = class_likelihood_ratios(y_test, y_pred)
print(f"LR+: {pos_LR:.3f}")
LR+: 12.617
بما أن نسبة الاحتمال الطبقي الإيجابية أكبر بكثير من 1.0، فهذا يعني أن أداة التشخيص القائمة على التعلم الآلي مفيدة: احتمالية ما بعد الاختبار أن الحالة موجودة بالفعل نظرًا لنتيجة الاختبار الإيجابية أكبر من 12 مرة من احتمالية ما قبل الاختبار.
التحقق المتقاطع لنسب الاحتمال الطبقي#
نقيم تباين القياسات لنسب الاحتمال الطبقي في بعض الحالات الخاصة.
import pandas as pd
def scoring(estimator, X, y):
y_pred = estimator.predict(X)
pos_lr, neg_lr = class_likelihood_ratios(y, y_pred, raise_warning=False)
return {"positive_likelihood_ratio": pos_lr, "negative_likelihood_ratio": neg_lr}
def extract_score(cv_results):
lr = pd.DataFrame(
{
"positive": cv_results["test_positive_likelihood_ratio"],
"negative": cv_results["test_negative_likelihood_ratio"],
}
)
return lr.aggregate(["mean", "std"])
نقوم أولاً بالتحقق من نموذج LogisticRegression
مع معاملات افتراضية كما هو مستخدم في القسم السابق.
from sklearn.model_selection import cross_validate
estimator = LogisticRegression()
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
نؤكد أن النموذج مفيد: احتمالية ما بعد الاختبار أكبر من 12 إلى 20 مرة من احتمالية ما قبل الاختبار.
على العكس، لنفترض نموذجًا وهميًا سيخرج تنبؤات عشوائية مع احتمالات مماثلة لمتوسط انتشار المرض في مجموعة التدريب:
from sklearn.dummy import DummyClassifier
estimator = DummyClassifier(strategy="stratified", random_state=1234)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
هنا كلتا نسبتي الاحتمال الطبقي متوافقتان مع 1.0 مما يجعل هذا المصنف عديم الفائدة كأداة تشخيصية لتحسين اكتشاف المرض.
خيار آخر للنموذج الوهمي هو التنبؤ دائمًا بالفئة الأكثر تكرارًا، والتي في هذه الحالة هي "عدم وجود مرض".
estimator = DummyClassifier(strategy="most_frequent")
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
عدم وجود تنبؤات إيجابية يعني أنه لن يكون هناك تنبؤات صحيحة ولا
تنبؤات خاطئة، مما يؤدي إلى نسبة احتمالية طبقية إيجابية غير محددة LR+
والتي لا ينبغي بأي حال تفسيرها كنسبة احتمالية طبقية إيجابية لا نهائية
(المصنف يحدد الحالات الإيجابية بشكل مثالي). في مثل هذه الحالة،
تقوم الدالة class_likelihood_ratios بإرجاع nan
وإظهار تحذير بشكل افتراضي. في الواقع، تساعدنا قيمة LR- على استبعاد هذا
النموذج.
قد ينشأ سيناريو مشابه عند التحقق المتقاطع لبيانات غير متوازنة للغاية مع عدد قليل من العينات: بعض الطيات لن يكون لديها عينات مع المرض وبالتالي لن تخرج تنبؤات صحيحة ولا تنبؤات خاطئة عند استخدامها للاختبار. رياضيًا، هذا يؤدي إلى نسبة احتمالية طبقية إيجابية لا نهائية، والتي لا ينبغي أيضًا تفسيرها على أنها النموذج الذي يحدد الحالات الإيجابية بشكل مثالي. مثل هذا الحدث يؤدي إلى تباين أعلى لنسب الاحتمال الطبقي المقدرة، ولكن يمكن تفسيرها على أنها زيادة في احتمالية ما بعد الاختبار لوجود الحالة.
estimator = LogisticRegression()
X, y = make_classification(n_samples=300, weights=[0.9, 0.1], random_state=0)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
الثبات فيما يتعلق بالانتشار#
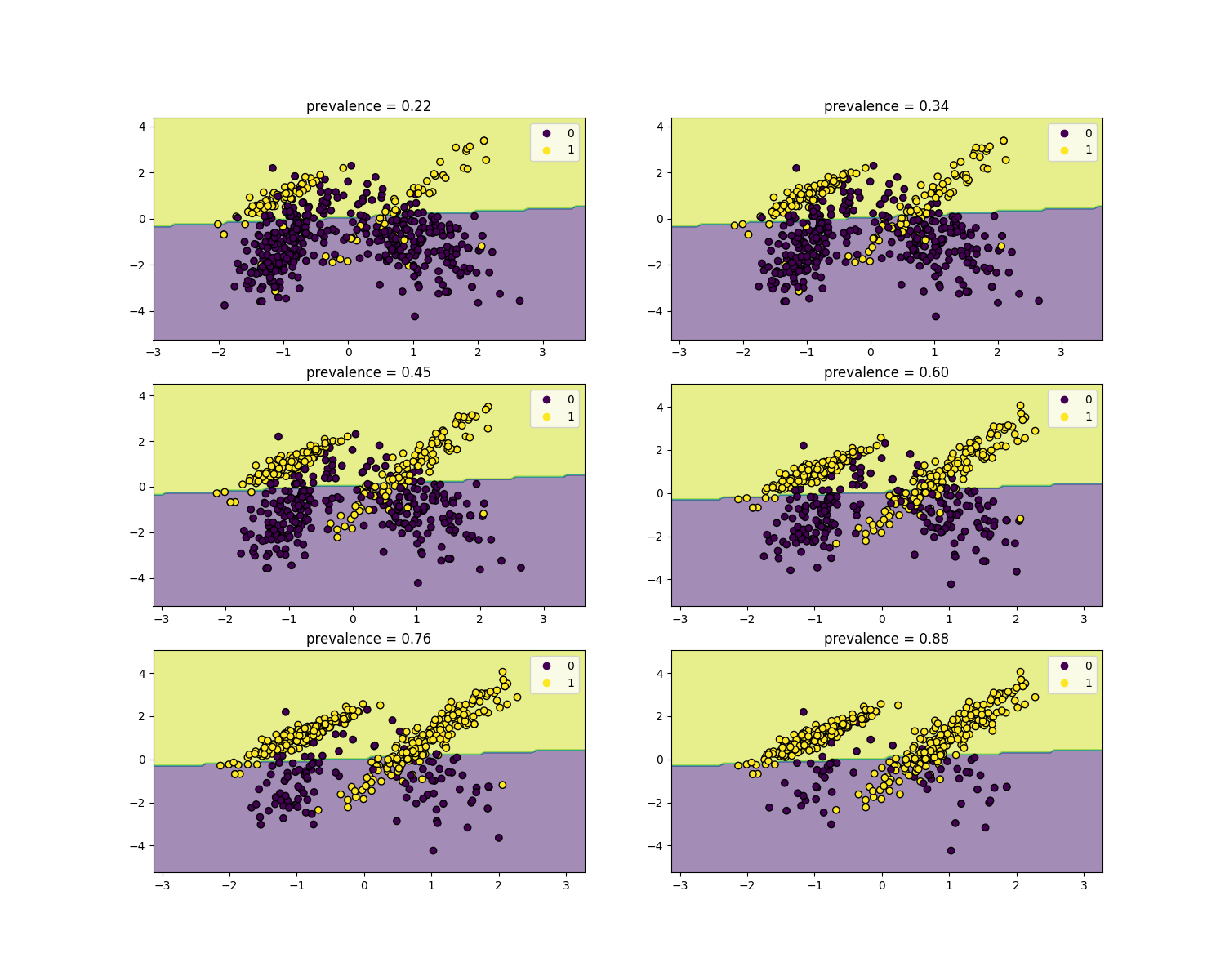
نسب الاحتمال الطبقي مستقلة عن انتشار المرض ويمكن استقراؤها بين السكان بغض النظر عن أي اختلال في التوازن بين الفئات، طالما يتم تطبيق نفس النموذج على جميع السكان. لاحظ أنه في الرسوم البيانية أدناه حدود القرار ثابتة (انظر SVM: المستوي الفاصل للطبقات غير المتوازنة لدراسة حدود القرار للتوازن غير المتوازن بين الفئات).
هنا نقوم بتدريب نموذج LogisticRegression
أساسي على دراسة حالة-مراقبة مع انتشار 50٪. ثم يتم تقييمه على
السكان مع انتشار متغير. نستخدم الدالة
make_classification لضمان أن
عملية توليد البيانات هي نفسها كما هو موضح في الرسوم البيانية أدناه.
التسمية 1 تقابل الفئة الإيجابية "المرض"، في حين أن التسمية 0
تقف على "عدم وجود مرض".
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
from sklearn.inspection import DecisionBoundaryDisplay
populations = defaultdict(list)
common_params = {
"n_samples": 10_000,
"n_features": 2,
"n_informative": 2,
"n_redundant": 0,
"random_state": 0,
}
weights = np.linspace(0.1, 0.8, 6)
weights = weights[::-1]
# ملاءمة وتقييم النموذج الأساسي على فئات متوازنة
X, y = make_classification(**common_params, weights=[0.5, 0.5])
estimator = LogisticRegression().fit(X, y)
lr_base = extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
pos_lr_base, pos_lr_base_std = lr_base["positive"].values
neg_lr_base, neg_lr_base_std = lr_base["negative"].values
سنعرض الآن حدود القرار لكل مستوى من مستويات الانتشار. لاحظ أننا نرسم فقط جزءًا من البيانات الأصلية لتقييم حدود القرار للنموذج الخطي بشكل أفضل.
fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(15, 12))
for ax, (n, weight) in zip(axs.ravel(), enumerate(weights)):
X, y = make_classification(
**common_params,
weights=[weight, 1 - weight],
)
prevalence = y.mean()
populations["prevalence"].append(prevalence)
populations["X"].append(X)
populations["y"].append(y)
# تقليل العينات للرسم
rng = np.random.RandomState(1)
plot_indices = rng.choice(np.arange(X.shape[0]), size=500, replace=True)
X_plot, y_plot = X[plot_indices], y[plot_indices]
# رسم حدود القرار الثابتة للنموذج الأساسي مع انتشار متغير
disp = DecisionBoundaryDisplay.from_estimator(
estimator,
X_plot,
response_method="predict",
alpha=0.5,
ax=ax,
)
scatter = disp.ax_.scatter(X_plot[:, 0], X_plot[:, 1], c=y_plot, edgecolor="k")
disp.ax_.set_title(f"prevalence = {y_plot.mean():.2f}")
disp.ax_.legend(*scatter.legend_elements())
نحدد دالة للتمهيد.
def scoring_on_bootstrap(estimator, X, y, rng, n_bootstrap=100):
results_for_prevalence = defaultdict(list)
for _ in range(n_bootstrap):
bootstrap_indices = rng.choice(
np.arange(X.shape[0]), size=X.shape[0], replace=True
)
for key, value in scoring(
estimator, X[bootstrap_indices], y[bootstrap_indices]
).items():
results_for_prevalence[key].append(value)
return pd.DataFrame(results_for_prevalence)
نقوم بتسجيل نقاط النموذج الأساسي لكل انتشار باستخدام التمهيد.
results = defaultdict(list)
n_bootstrap = 100
rng = np.random.default_rng(seed=0)
for prevalence, X, y in zip(
populations["prevalence"], populations["X"], populations["y"]
):
results_for_prevalence = scoring_on_bootstrap(
estimator, X, y, rng, n_bootstrap=n_bootstrap
)
results["prevalence"].append(prevalence)
results["metrics"].append(
results_for_prevalence.aggregate(["mean", "std"]).unstack()
)
results = pd.DataFrame(results["metrics"], index=results["prevalence"])
results.index.name = "prevalence"
results
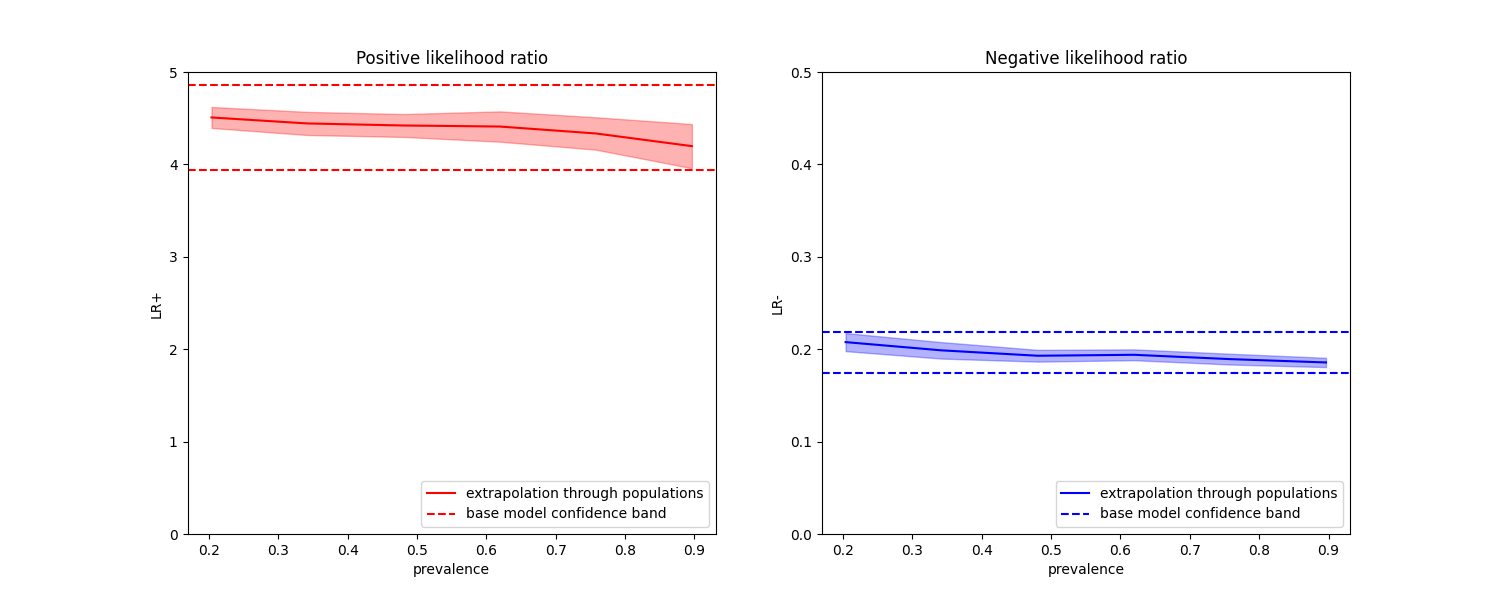
في الرسوم البيانية أدناه، نلاحظ أن نسب الاحتمال الطبقي المعاد حسابها مع انتشار مختلف ثابتة ضمن انحراف معياري واحد من تلك المحسوبة على فئات متوازنة.
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(15, 6))
results["positive_likelihood_ratio"]["mean"].plot(
ax=ax1, color="r", label="extrapolation through populations"
)
ax1.axhline(y=pos_lr_base + pos_lr_base_std, color="r", linestyle="--")
ax1.axhline(
y=pos_lr_base - pos_lr_base_std,
color="r",
linestyle="--",
label="base model confidence band",
)
ax1.fill_between(
results.index,
results["positive_likelihood_ratio"]["mean"]
- results["positive_likelihood_ratio"]["std"],
results["positive_likelihood_ratio"]["mean"]
+ results["positive_likelihood_ratio"]["std"],
color="r",
alpha=0.3,
)
ax1.set(
title="Positive likelihood ratio",
ylabel="LR+",
ylim=[0, 5],
)
ax1.legend(loc="lower right")
ax2 = results["negative_likelihood_ratio"]["mean"].plot(
ax=ax2, color="b", label="extrapolation through populations"
)
ax2.axhline(y=neg_lr_base + neg_lr_base_std, color="b", linestyle="--")
ax2.axhline(
y=neg_lr_base - neg_lr_base_std,
color="b",
linestyle="--",
label="base model confidence band",
)
ax2.fill_between(
results.index,
results["negative_likelihood_ratio"]["mean"]
- results["negative_likelihood_ratio"]["std"],
results["negative_likelihood_ratio"]["mean"]
+ results["negative_likelihood_ratio"]["std"],
color="b",
alpha=0.3,
)
ax2.set(
title="Negative likelihood ratio",
ylabel="LR-",
ylim=[0, 0.5],
)
ax2.legend(loc="lower right")
plt.show()
Total running time of the script: (0 minutes 2.040 seconds)
Related examples