ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
عدم الملاءمة مقابل الإفراط في الملاءمة#
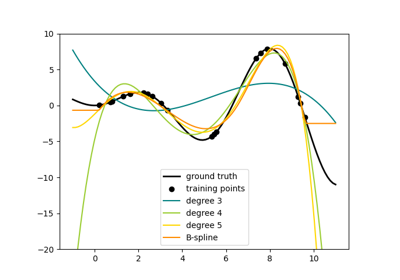
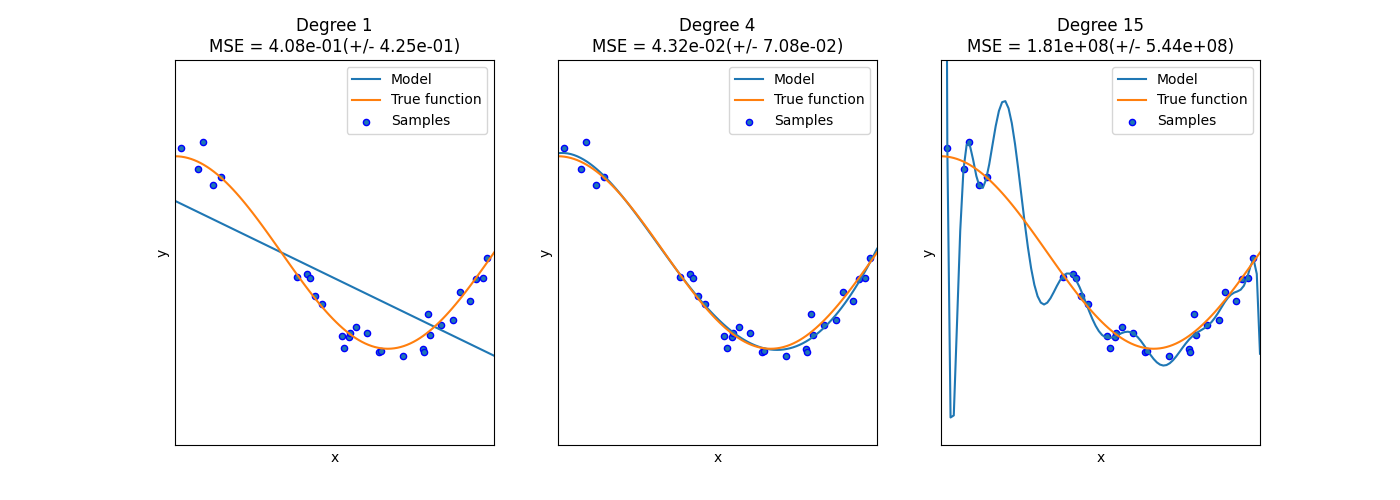
هذا المثال يوضح مشكلتي عدم الملاءمة والإفراط في الملاءمة وكيف يمكننا استخدام الانحدار الخطي مع الميزات متعددة الحدود لتقريب الدوال غير الخطية. يوضح الرسم البياني الدالة التي نريد تقريبها، والتي هي جزء من دالة جيب التمام. بالإضافة إلى ذلك، يتم عرض العينات من الدالة الحقيقية وتقديرات النماذج المختلفة. تمتلك النماذج ميزات متعددة الحدود بدرجات مختلفة. يمكننا أن نرى أن الدالة الخطية (متعددة الحدود من الدرجة 1) غير كافية لملاءمة العينات التدريبية. يُطلق على هذا عدم الملاءمة. تقترب متعددة الحدود من الدرجة 4 من الدالة الحقيقية بشكل مثالي تقريبًا. ومع ذلك، بالنسبة للدرجات الأعلى، فإن النموذج سوف يبالغ في الملاءمة لبيانات التدريب، أي أنه يتعلم ضوضاء بيانات التدريب.
نقيّم الإفراط في الملاءمة و عدم الملاءمة بشكل كمي باستخدام التحقق المتقاطع. نحسب متوسط مربع الخطأ (MSE) على مجموعة التحقق، كلما كان أعلى، كلما قلت احتمالية تعميم النموذج بشكل صحيح من بيانات التدريب.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def true_fun(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
degrees = [1, 4, 15]
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline(
[
("polynomial_features", polynomial_features),
("linear_regression", linear_regression),
]
)
pipeline.fit(X[:, np.newaxis], y)
# تقييم النماذج باستخدام التحقق المتقاطع
scores = cross_val_score(
pipeline, X[:, np.newaxis], y, scoring="neg_mean_squared_error", cv=10
)
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X, y, edgecolor="b", s=20, label="Samples")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title(
"Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
degrees[i], -scores.mean(), scores.std()
)
)
plt.show()
Total running time of the script: (0 minutes 0.243 seconds)
Related examples
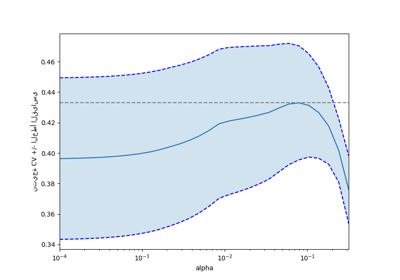
التحقق المتقاطع على تمرين مجموعة بيانات مرض السكري