ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
ضبط عتبة القرار للتعلم الحساس للتكلفة#
بمجرد تدريب المصنف، فإن ناتج طريقة predict ينتج تنبؤات تسمية الفئة المقابلة لعتبة إما decision_function أو ناتج predict_proba. بالنسبة للمصنف الثنائي، فإن العتبة الافتراضية محددة كتقدير احتمالية لاحقة تبلغ 0.5 أو درجة قرار تبلغ 0.0.
ومع ذلك، من المحتمل ألا تكون هذه الاستراتيجية الافتراضية هي الأمثل للمهمة قيد التنفيذ. هنا، نستخدم مجموعة بيانات "Statlog" الألمانية للائتمان [1] لتوضيح حالة استخدام.
في هذه المجموعة من البيانات، تتمثل المهمة في التنبؤ بما إذا كان الشخص لديه ائتمان "جيد" أو "سيء". بالإضافة إلى ذلك، يتم توفير مصفوفة التكلفة التي تحدد تكلفة التصنيف الخاطئ. على وجه التحديد، فإن تصنيف ائتمان "سيء" على أنه "جيد" هو خمسة أضعاف متوسط تكلفة تصنيف ائتمان "جيد" على أنه "سيء".
نستخدم TunedThresholdClassifierCV لتحديد نقطة قطع وظيفة القرار التي تقلل التكلفة التجارية المقدمة.
في الجزء الثاني من المثال، نقوم بتوسيع هذا النهج أكثر من خلال النظر في مشكلة اكتشاف الاحتيال في معاملات بطاقات الائتمان: في هذه الحالة، تعتمد المقياس التجاري على مبلغ كل معاملة فردية.
المراجع
# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause
التعلم الحساس للتكلفة مع المكاسب والتكاليف الثابتة#
في هذا القسم الأول، نوضح استخدام
TunedThresholdClassifierCV في إعداد
التعلم الحساس للتكلفة عندما تكون المكاسب والتكاليف المرتبطة بكل إدخال في مصفوفة الارتباك ثابتة. نستخدم المشكلة المقدمة في [2] باستخدام
مجموعة بيانات "Statlog" الألمانية للائتمان [1].
مجموعة بيانات "Statlog" الألمانية للائتمان#
نستخرج مجموعة بيانات الائتمان الألمانية من OpenML.
import sklearn
from sklearn.datasets import fetch_openml
sklearn.set_config(transform_output="pandas")
german_credit = fetch_openml(data_id=31, as_frame=True, parser="pandas")
X, y = german_credit.data, german_credit.target
نتحقق من أنواع الميزات المتوفرة في X.
X.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 20 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 checking_status 1000 non-null category
1 duration 1000 non-null int64
2 credit_history 1000 non-null category
3 purpose 1000 non-null category
4 credit_amount 1000 non-null int64
5 savings_status 1000 non-null category
6 employment 1000 non-null category
7 installment_commitment 1000 non-null int64
8 personal_status 1000 non-null category
9 other_parties 1000 non-null category
10 residence_since 1000 non-null int64
11 property_magnitude 1000 non-null category
12 age 1000 non-null int64
13 other_payment_plans 1000 non-null category
14 housing 1000 non-null category
15 existing_credits 1000 non-null int64
16 job 1000 non-null category
17 num_dependents 1000 non-null int64
18 own_telephone 1000 non-null category
19 foreign_worker 1000 non-null category
dtypes: category(13), int64(7)
memory usage: 69.9 KB
العديد من الميزات هي فئات وعادة ما تكون مشفرة بالسلاسل. نحتاج إلى تشفير هذه الفئات عندما نطور نموذجنا التنبؤي. دعنا نتحقق من الأهداف.
y.value_counts()
class
good 700
bad 300
Name: count, dtype: int64
ملاحظة أخرى هي أن مجموعة البيانات غير متوازنة. نحتاج إلى توخي الحذر عند تقييم نموذجنا التنبؤي واستخدام عائلة من المقاييس التي تتكيف مع هذا الإعداد.
بالإضافة إلى ذلك، نلاحظ أن الهدف مشفر بالسلاسل. بعض المقاييس (مثل الدقة والاستدعاء) تتطلب توفير تسمية "الإيجابية" أيضًا تسمى "التسمية الإيجابية". هنا، نحدد أن هدفنا هو التنبؤ بما إذا كان أو لم يكن عينة "ائتمان سيء".
pos_label, neg_label = "bad", "good"
للقيام بتحليلنا، نقسم مجموعتنا باستخدام تقسيم مفرد متوازن.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
نحن مستعدون لتصميم نموذجنا التنبؤي واستراتيجية التقييم المرتبطة به.
مقاييس التقييم#
في هذا القسم، نحدد مجموعة من المقاييس التي نستخدمها لاحقًا. لرؤية تأثير ضبط نقطة القطع، نقيم النموذج التنبؤي باستخدام منحنى خصائص التشغيل المتلقي (ROC) ومنحنى الدقة والاستدعاء. القيم المبلغ عنها على هذه الرسوم البيانية هي لذلك معدل الإيجابية الحقيقية (TPR)، المعروف أيضًا بالاستدعاء أو الحساسية، ومعدل الإيجابية الخاطئة (FPR)، المعروف أيضًا بالخصوصية، بالنسبة لمنحنى ROC والدقة والاستدعاء لمنحنى الدقة والاستدعاء.
من بين هذه المقاييس الأربعة، لا يوفر scikit-learn أداة تسجيل نقاط لـ FPR. نحن لذلك نحتاج إلى تعريف دالة مخصصة صغيرة لحسابها.
from sklearn.metrics import confusion_matrix
def fpr_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
tn, fp, _, _ = cm.ravel()
tnr = tn / (tn + fp)
return 1 - tnr
كما ذكر سابقًا، لا يتم تعريف "التسمية الإيجابية" على أنها القيمة "1" واستدعاء بعض المقاييس مع هذه القيمة غير القياسية ترفع خطأ. نحتاج إلى تقديم مؤشر "التسمية الإيجابية" إلى المقاييس.
لذلك نحتاج إلى تعريف أداة تسجيل نقاط scikit-learn باستخدام
make_scorer حيث يتم تمرير المعلومات. نحن نخزن جميع
أدوات تسجيل النقاط المخصصة في قاموس. لاستخدامها، نحتاج إلى تمرير النموذج المناسب،
البيانات والهدف الذي نريد تقييم النموذج التنبؤي عليه.
from sklearn.metrics import make_scorer, precision_score, recall_score
tpr_score = recall_score # TPR والاستدعاء هما نفس المقياس
scoring = {
"precision": make_scorer(precision_score, pos_label=pos_label),
"recall": make_scorer(recall_score, pos_label=pos_label),
"fpr": make_scorer(fpr_score, neg_label=neg_label, pos_label=pos_label),
"tpr": make_scorer(tpr_score, pos_label=pos_label),
}
بالإضافة إلى ذلك، تحدد الأبحاث الأصلية [1] مقياسًا تجاريًا مخصصًا. نحن ندعو "المقياس التجاري" أي دالة مقياس تهدف إلى تحديد الكمية كيف يمكن للتنبؤات (الصحيحة أو الخاطئة) أن تؤثر على القيمة التجارية لنشر نموذج تعلم آلي معين في سياق تطبيق محدد. لمهمتنا مهمة التنبؤ بالائتمان، يقدم المؤلفون مصفوفة تكلفة مخصصة والتي تشفر أن تصنيف ائتمان "سيء" على أنه "جيد" هو 5 مرات أكثر تكلفة في المتوسط من العكس: إنه أقل تكلفة لمؤسسة التمويل لعدم منح ائتمان لعميل محتمل لن يتخلف عن السداد (وبالتالي تفويت عميل جيد كان سيسدد الائتمان ويدفع الفوائد) من منح الائتمان لعميل سيتخلف عن السداد.
نحن نحدد دالة بايثون تزن مصفوفة الارتباك وتعيد التكلفة الإجمالية.
import numpy as np
def credit_gain_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
# تحتوي صفوف مصفوفة الارتباك على عدد الفئات الملاحظة
# في حين تحتوي الأعمدة على عدد الفئات المتوقعة. تذكر أننا هنا
# نعتبر "سيء" على أنه الفئة الإيجابية (الصف الثاني والعمود).
# تتوقع أدوات اختيار النموذج في scikit-learn أننا نتبع اتفاقية
# أن "الأعلى" يعني "الأفضل"، وبالتالي فإن مصفوفة المكاسب التالية تعين
# مكاسب سلبية (تكاليف) لنوعين من أخطاء التنبؤ:
# - مكسب -1 لكل إيجابية خاطئة ("ائتمان جيد" مصنف على أنه "سيء")،
# - مكسب -5 لكل سلبية خاطئة ("ائتمان سيء" مصنف على أنه "جيد")،
# يتم تعيين المكاسب الصحيحة والسلبيات على مكاسب صفرية في هذا
# المقياس.
#
# لاحظ أنه نظريًا، نظرًا لأن نموذجنا معايرة ومجموعة بياناتنا
# ممثل وكبير بما فيه الكفاية، لا نحتاج إلى ضبط العتبة، ولكن يمكننا تعيينها بأمان
# إلى نسبة التكلفة 1/5، كما ذكرت المعادلة.
# (2) في ورقة Elkan [2]_.
gain_matrix = np.array(
[
[0, -1], # مكسب -1 للإيجابيات الخاطئة
[-5, 0], # مكسب -5 للسلبيات الخاطئة
]
)
return np.sum(cm * gain_matrix)
scoring["credit_gain"] = make_scorer(
credit_gain_score, neg_label=neg_label, pos_label=pos_label
)
نموذج تنبؤي بسيط#
نستخدم HistGradientBoostingClassifier كنموذج تنبؤي
الذي يتعامل بشكل أصلي مع الميزات الفئوية والقيم المفقودة.
from sklearn.ensemble import HistGradientBoostingClassifier
model = HistGradientBoostingClassifier(
categorical_features="from_dtype", random_state=0
).fit(X_train, y_train)
model
نقيم أداء نموذجنا التنبؤي باستخدام منحنى ROC ومنحنى الدقة والاستدعاء.
import matplotlib.pyplot as plt
from sklearn.metrics import PrecisionRecallDisplay, RocCurveDisplay
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
PrecisionRecallDisplay.from_estimator(
model, X_test, y_test, pos_label=pos_label, ax=axs[0], name="GBDT"
)
axs[0].plot(
scoring["recall"](model, X_test, y_test),
scoring["precision"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="نقطة قطع افتراضية عند احتمال 0.5",
)
axs[0].set_title("منحنى الدقة والاستدعاء")
axs[0].legend()
RocCurveDisplay.from_estimator(
model,
X_test,
y_test,
pos_label=pos_label,
ax=axs[1],
name="GBDT",
plot_chance_level=True,
)
axs[1].plot(
scoring["fpr"](model, X_test, y_test),
scoring["tpr"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="نقطة قطع افتراضية عند احتمال 0.5",
)
axs[1].set_title("منحنى ROC")
axs[1].legend()
_ = fig.suptitle("تقييم نموذج GBDT البسيط")
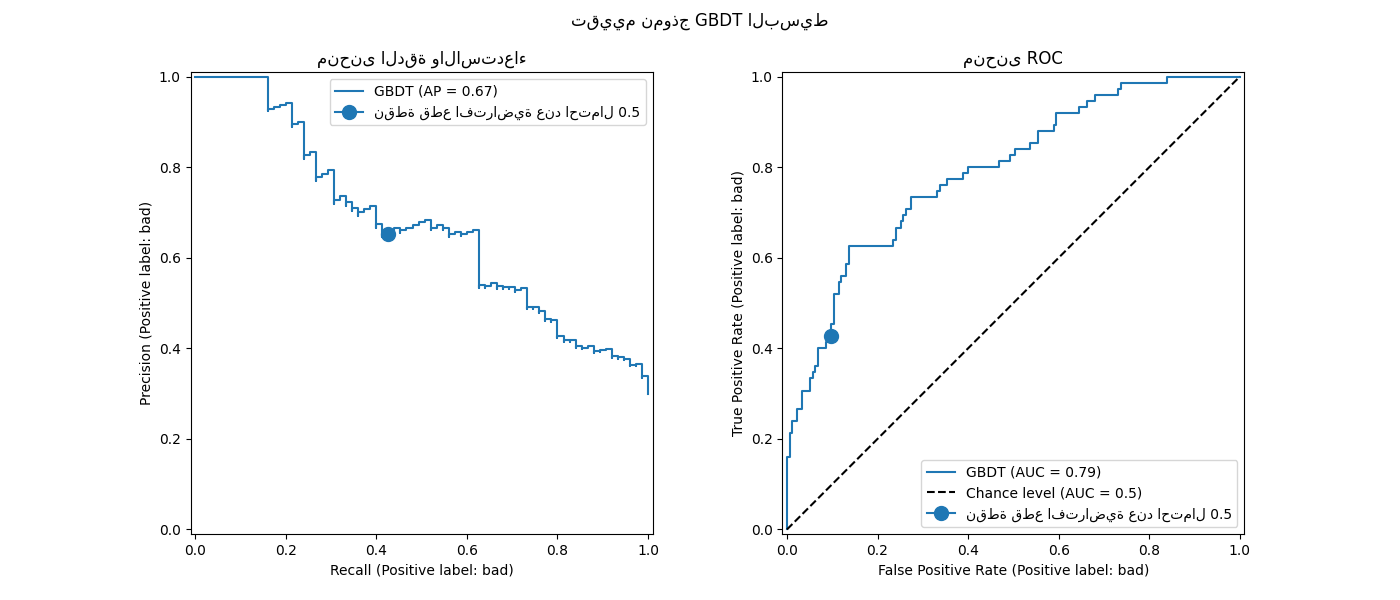
نذكر أن هذه المنحنيات توفر نظرة ثاقبة على الأداء الإحصائي النموذج التنبؤي لنقاط القطع المختلفة. بالنسبة لمنحنى الدقة والاستدعاء، المقاييس المبلغ عنها هي الدقة والاستدعاء ولمنحنى ROC، المقاييس المبلغ عنها هي TPR (نفس الاستدعاء) وFPR.
هنا، تتوافق نقاط القطع المختلفة مع مستويات مختلفة من تقديرات الاحتمالية اللاحقة تتراوح بين 0 و1. بشكل افتراضي، يستخدم model.predict نقطة قطع عند تقدير الاحتمالية 0.5. يتم الإبلاغ عن المقاييس لمثل هذه نقطة القطع
مع النقطة الزرقاء على المنحنيات: إنه يتوافق مع الأداء الإحصائي
النموذج عند استخدام model.predict.
ومع ذلك، نذكر أن الهدف الأصلي كان تقليل التكلفة (أو زيادة المكاسب) كما هو محدد بالمقياس التجاري. يمكننا حساب قيمة المقياس التجاري:
print(f"المقياس التجاري المحدد: {scoring['credit_gain'](model, X_test, y_test)}")
المقياس التجاري المحدد: -232
في هذه المرحلة، لا نعرف ما إذا كانت أي نقطة قطع أخرى يمكن أن تؤدي إلى مكاسب أكبر. للعثور على
نقطة القطع المثلى، نحتاج إلى حساب التكلفة-المكسب باستخدام المقياس التجاري لجميع
نقاط القطع الممكنة واختيار الأفضل. يمكن أن تكون هذه الاستراتيجية مرهقة للغاية لتنفيذها
باليد، ولكن
TunedThresholdClassifierCV هنا لمساعدتنا.
يحسب تلقائيًا التكلفة-المكسب لجميع نقاط القطع الممكنة ويحسن
للـ scoring.
ضبط نقطة القطع#
نستخدم TunedThresholdClassifierCV لضبط
نقطة القطع. نحتاج إلى توفير المقياس التجاري لتحسينه بالإضافة إلى
التسمية الإيجابية. داخليًا، يتم اختيار نقطة القطع المثلى بحيث تزيد من
المقياس التجاري عبر التحقق من الصحة. بشكل افتراضي، يتم استخدام التحقق من الصحة المتقاطع 5 أضعاف.
from sklearn.model_selection import TunedThresholdClassifierCV
tuned_model = TunedThresholdClassifierCV(
estimator=model,
scoring=scoring["credit_gain"],
store_cv_results=True, # ضروري لفحص جميع النتائج
)
tuned_model.fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.02
نرسم منحنى ROC ومنحنى الدقة والاستدعاء للنموذج البسيط والنموذج المضبوط. أيضًا نرسم نقاط القطع التي سيستخدمها كل نموذج. نظرًا لأننا نعيد استخدام نفس الكود لاحقًا، فإننا نحدد دالة تولد الرسوم البيانية.
def plot_roc_pr_curves(vanilla_model, tuned_model, *, title):
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(21, 6))
linestyles = ("dashed", "dotted")
markerstyles = ("o", ">")
colors = ("tab:blue", "tab:orange")
names = ("Vanilla GBDT", "Tuned GBDT")
for idx, (est, linestyle, marker, color, name) in enumerate(
zip((vanilla_model, tuned_model), linestyles, markerstyles, colors, names)
):
decision_threshold = getattr(est, "best_threshold_", 0.5)
PrecisionRecallDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
linestyle=linestyle,
color=color,
ax=axs[0],
name=name,
)
axs[0].plot(
scoring["recall"](est, X_test, y_test),
scoring["precision"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
RocCurveDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
linestyle=linestyle,
color=color,
ax=axs[1],
name=name,
plot_chance_level=idx == 1,
)
axs[1].plot(
scoring["fpr"](est, X_test, y_test),
scoring["tpr"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
axs[0].set_title("Precision-Recall curve")
axs[0].legend()
axs[1].set_title("ROC curve")
axs[1].legend()
axs[2].plot(
tuned_model.cv_results_["thresholds"],
tuned_model.cv_results_["scores"],
color="tab:orange",
)
axs[2].plot(
tuned_model.best_threshold_,
tuned_model.best_score_,
"o",
markersize=10,
color="tab:orange",
label="Optimal cut-off point for the business metric",
)
axs[2].legend()
axs[2].set_xlabel("Decision threshold (probability)")
axs[2].set_ylabel("Objective score (using cost-matrix)")
axs[2].set_title("Objective score as a function of the decision threshold")
fig.suptitle(title)
title = "Comparison of the cut-off point for the vanilla and tuned GBDT model"
plot_roc_pr_curves(model, tuned_model, title=title)
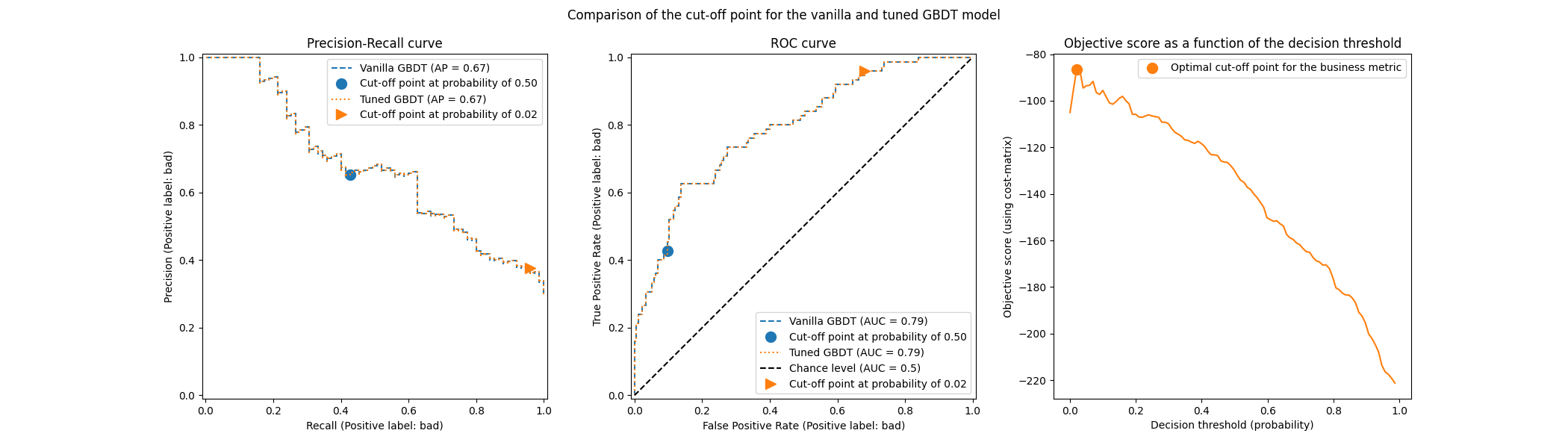
نلاحظ أن كلا المصنفين لهما نفس منحنيات ROC و Precision-Recall تمامًا. هذا متوقع لأن المصنف، افتراضيًا، ملائم على نفس بيانات التدريب. في قسم لاحق، نناقش بمزيد من التفصيل الخيارات المتاحة فيما يتعلق بإعادة ملاءمة النموذج والتحقق المتقاطع.
الملاحظة الثانية هي أن نقاط القطع للنموذج العادي والنموذج المضبوط مختلفة. لفهم سبب اختيار النموذج المضبوط لنقطة القطع هذه، يمكننا إلقاء نظرة على الرسم البياني على الجانب الأيمن الذي يرسم درجة الهدف التي هي نفسها تمامًا مقياس أعمالنا. نرى أن العتبة المثلى تتوافق مع الحد الأقصى لدرجة الهدف. يتم الوصول إلى هذا الحد الأقصى لعتبة قرار أقل بكثير من 0.5: يتمتع النموذج المضبوط باستدعاء أعلى بكثير على حساب دقة أقل بكثير: النموذج المضبوط أكثر حرصًا على التنبؤ بتصنيف "سيئ" لنسبة أكبر من الأفراد.
يمكننا الآن التحقق مما إذا كان اختيار نقطة القطع هذه يؤدي إلى درجة أفضل على مجموعة الاختبار:
print(f"المقياس المحدد للأعمال: {scoring['credit_gain'](tuned_model, X_test, y_test)}")
المقياس المحدد للأعمال: -134
نلاحظ أن ضبط عتبة القرار يحسن تقريبًا مكاسب أعمالنا بمعامل 2.
اعتبارات تتعلق بإعادة ملاءمة النموذج والتحقق المتقاطع#
في التجربة أعلاه، استخدمنا الإعداد الافتراضي لـ
TunedThresholdClassifierCV. على وجه الخصوص،
يتم ضبط نقطة القطع باستخدام تحقق متقاطع طبقي من 5 طيات. أيضًا،
تتم إعادة ملاءمة نموذج التنبؤ الأساسي على بيانات التدريب بأكملها بمجرد
اختيار نقطة القطع.
يمكن تغيير هاتين الاستراتيجيتين من خلال توفير معلمات refit و cv.
على سبيل المثال، يمكن للمرء توفير estimator ملائم وتعيين cv="prefit"، وفي
هذه الحالة يتم العثور على نقطة القطع على مجموعة البيانات بأكملها المقدمة في وقت
الملاءمة. أيضًا، لا تتم إعادة ملاءمة المصنف الأساسي عن طريق تعيين refit=False.
هنا، يمكننا محاولة إجراء مثل هذه التجربة.
model.fit(X_train, y_train)
tuned_model.set_params(cv="prefit", refit=False).fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.28
ثم نقوم بتقييم نموذجنا بنفس الطريقة السابقة:
title = "نموذج GBDT مضبوط بدون إعادة ملاءمة وباستخدام مجموعة البيانات بأكملها"
plot_roc_pr_curves(model, tuned_model, title=title)
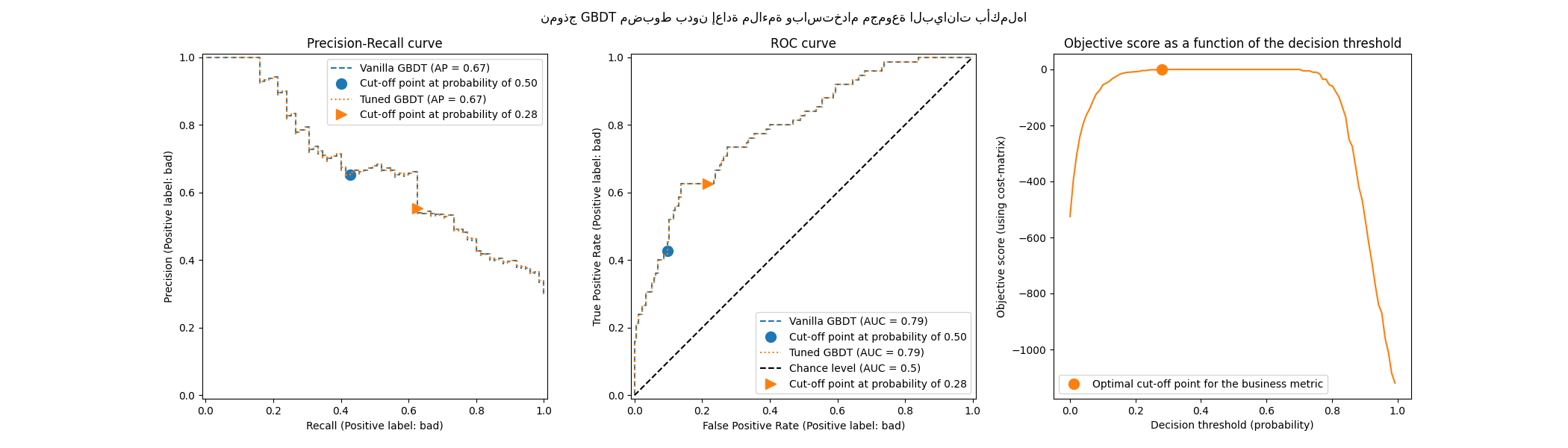
نلاحظ أن نقطة القطع المثلى تختلف عن تلك التي تم العثور عليها في التجربة السابقة. إذا نظرنا إلى الرسم البياني على الجانب الأيمن، نلاحظ أن مكسب العمل له هضبة كبيرة من المكاسب شبه المثلى 0 لفترة زمنية كبيرة من عتبات القرار. هذا السلوك من أعراض فرط التخصيص. نظرًا لأننا قمنا بتعطيل التحقق المتقاطع، فقد قمنا بضبط نقطة القطع على نفس المجموعة التي تم تدريب النموذج عليها، وهذا هو سبب فرط التخصيص الملحوظ.
لذلك يجب استخدام هذا الخيار بحذر. يجب على المرء التأكد من أن
البيانات المقدمة في وقت الملاءمة إلى
TunedThresholdClassifierCV ليست هي نفس
البيانات المستخدمة لتدريب المصنف الأساسي. قد يحدث هذا أحيانًا عندما تكون
الفكرة هي مجرد ضبط نموذج التنبؤ على مجموعة تحقق جديدة تمامًا بدون
إعادة ملاءمة كاملة مكلفة.
عندما يكون التحقق المتقاطع مكلفًا للغاية، يتمثل أحد البدائل المحتملة في استخدام
تقسيم واحد للتدريب والاختبار من خلال توفير رقم عائم في النطاق [0، 1] لمعلمة cv.
يقوم بتقسيم البيانات إلى مجموعة تدريب ومجموعة اختبار. دعونا نستكشف هذا
الخيار:
tuned_model.set_params(cv=0.75).fit(X_train, y_train)
title = "نموذج GBDT مضبوط بدون إعادة ملاءمة وباستخدام مجموعة البيانات بأكملها"
plot_roc_pr_curves(model, tuned_model, title=title)
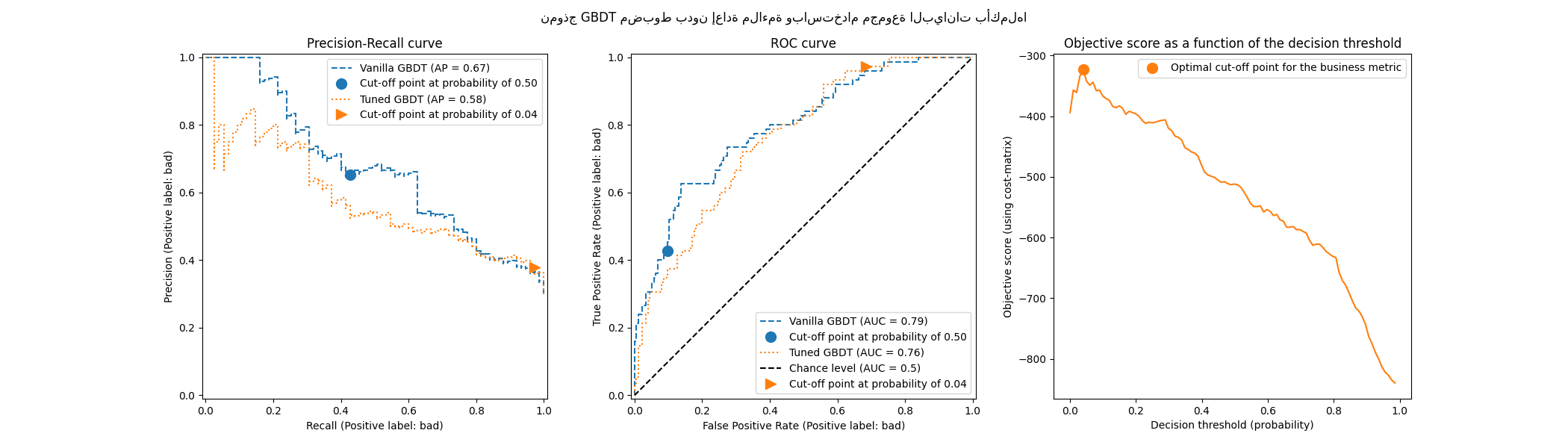
فيما يتعلق بنقطة القطع، نلاحظ أن النقطة المثلى تشبه حالة التحقق المتقاطع المتكرر المتعدد. ومع ذلك، يجب أن تدرك أن التقسيم الفردي لا يفسر تقلب عملية الملاءمة / التنبؤ، وبالتالي لا يمكننا معرفة ما إذا كان هناك أي تباين في نقطة القطع. يقوم التحقق المتقاطع المتكرر بمتوسط هذا التأثير.
تتعلق ملاحظة أخرى بمنحنيات ROC و Precision-Recall للنموذج المضبوط. كما هو متوقع، تختلف هذه المنحنيات عن منحنيات النموذج العادي، نظرًا لأننا دربنا المصنف الأساسي على مجموعة فرعية من البيانات المقدمة أثناء الملاءمة وحجزنا مجموعة تحقق لضبط نقطة القطع.
التعلم الحساس للتكلفة عندما لا تكون المكاسب والتكاليف ثابتة#
كما هو مذكور في [2]، فإن المكاسب والتكاليف ليست ثابتة بشكل عام في مشاكل العالم الحقيقي. في هذا القسم، نستخدم مثالًا مشابهًا كما في [2] لمشكلة اكتشاف الاحتيال في سجلات معاملات بطاقات الائتمان.
مجموعة بيانات بطاقة الائتمان#
credit_card = fetch_openml(data_id=1597, as_frame=True, parser="pandas")
credit_card.frame.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 30 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 284807 non-null float64
1 V2 284807 non-null float64
2 V3 284807 non-null float64
3 V4 284807 non-null float64
4 V5 284807 non-null float64
5 V6 284807 non-null float64
6 V7 284807 non-null float64
7 V8 284807 non-null float64
8 V9 284807 non-null float64
9 V10 284807 non-null float64
10 V11 284807 non-null float64
11 V12 284807 non-null float64
12 V13 284807 non-null float64
13 V14 284807 non-null float64
14 V15 284807 non-null float64
15 V16 284807 non-null float64
16 V17 284807 non-null float64
17 V18 284807 non-null float64
18 V19 284807 non-null float64
19 V20 284807 non-null float64
20 V21 284807 non-null float64
21 V22 284807 non-null float64
22 V23 284807 non-null float64
23 V24 284807 non-null float64
24 V25 284807 non-null float64
25 V26 284807 non-null float64
26 V27 284807 non-null float64
27 V28 284807 non-null float64
28 Amount 284807 non-null float64
29 Class 284807 non-null category
dtypes: category(1), float64(29)
memory usage: 63.3 MB
تحتوي مجموعة البيانات على معلومات حول سجلات بطاقات الائتمان التي يكون بعضها احتياليًا والبعض الآخر شرعيًا. الهدف إذن هو التنبؤ بما إذا كان سجل بطاقة الائتمان احتياليًا أم لا.
columns_to_drop = ["Class"]
data = credit_card.frame.drop(columns=columns_to_drop)
target = credit_card.frame["Class"].astype(int)
أولاً، نتحقق من توزيع الفئات لمجموعات البيانات.
target.value_counts(normalize=True)
Class
0 0.998273
1 0.001727
Name: proportion, dtype: float64
مجموعة البيانات غير متوازنة للغاية حيث تمثل المعاملة الاحتيالية 0.17% فقط من البيانات. نظرًا لأننا مهتمون بتدريب نموذج تعلم آلي، يجب أن نتأكد أيضًا من أن لدينا عينات كافية في فئة الأقلية لتدريب النموذج.
target.value_counts()
Class
0 284315
1 492
Name: count, dtype: int64
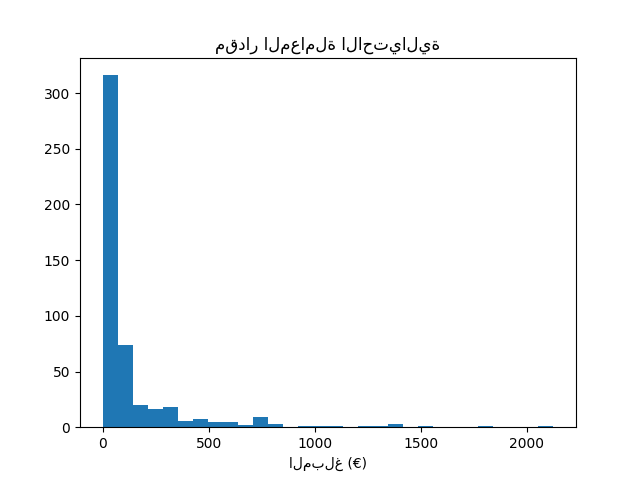
نلاحظ أن لدينا حوالي 500 عينة وهي في الطرف الأدنى من عدد العينات المطلوبة لتدريب نموذج تعلم آلي. بالإضافة إلى توزيع الهدف، نتحقق من توزيع مقدار المعاملات الاحتيالية.
fraud = target == 1
amount_fraud = data["Amount"][fraud]
_, ax = plt.subplots()
ax.hist(amount_fraud, bins=30)
ax.set_title("مقدار المعاملة الاحتيالية")
_ = ax.set_xlabel("المبلغ (€)")
معالجة المشكلة بمقياس أعمال#
الآن، نقوم بإنشاء مقياس أعمال يعتمد على مقدار كل معاملة. نحدد مصفوفة التكلفة بشكل مشابه لـ [2]. يوفر قبول معاملة شرعية ربحًا بنسبة 2% من مبلغ المعاملة. ومع ذلك، فإن قبول معاملة احتيالية يؤدي إلى خسارة مبلغ المعاملة. كما هو مذكور في [2]، فإن الربح والخسارة المتعلقين بالرفض (للمعاملات الاحتيالية والشرعية) ليس من السهل تعريفها. هنا، نحدد أن رفض معاملة شرعية يُقدر بخسارة 5 يورو بينما يُقدر رفض معاملة احتيالية بربح 50 يورو. لذلك، نحدد الوظيفة التالية لحساب إجمالي فائدة قرار معين:
def business_metric(y_true, y_pred, amount):
mask_true_positive = (y_true == 1) & (y_pred == 1)
mask_true_negative = (y_true == 0) & (y_pred == 0)
mask_false_positive = (y_true == 0) & (y_pred == 1)
mask_false_negative = (y_true == 1) & (y_pred == 0)
fraudulent_refuse = mask_true_positive.sum() * 50
fraudulent_accept = -amount[mask_false_negative].sum()
legitimate_refuse = mask_false_positive.sum() * -5
legitimate_accept = (amount[mask_true_negative] * 0.02).sum()
return fraudulent_refuse + fraudulent_accept + legitimate_refuse + legitimate_accept
من مقياس الأعمال هذا، نقوم بإنشاء مسجل scikit-learn الذي يقوم، نظرًا لمصنف
ملائم ومجموعة اختبار، بحساب مقياس الأعمال. في هذا الصدد، نستخدم
المصنع make_scorer. المتغير amount هو
بيانات وصفية إضافية يتم تمريرها إلى المسجل ونحتاج إلى استخدام
توجيه البيانات الوصفية لمراعاة هذه المعلومات.
sklearn.set_config(enable_metadata_routing=True)
business_scorer = make_scorer(business_metric).set_score_request(amount=True)
لذلك في هذه المرحلة، نلاحظ أن مقدار المعاملة يُستخدم مرتين: مرة
واحدة كميزة لتدريب نموذج التنبؤ الخاص بنا ومرة واحدة كبيانات وصفية
لحساب مقياس الأعمال وبالتالي الأداء الإحصائي لنموذجنا. عند استخدامه
كميزة، لا يُطلب منا سوى أن يكون لدينا عمود في data يحتوي على مقدار
كل معاملة. لاستخدام هذه المعلومات كبيانات وصفية، نحتاج إلى متغير
خارجي يمكننا تمريره إلى المسجل أو النموذج الذي يقوم داخليًا بتوجيه
هذه البيانات الوصفية إلى المسجل. لذلك دعونا ننشئ هذا المتغير.
amount = credit_card.frame["Amount"].to_numpy()
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test, amount_train, amount_test = (
train_test_split(
data, target, amount, stratify=target, test_size=0.5, random_state=42
)
)
نقوم أولاً بتقييم بعض سياسات خط الأساس لتكون بمثابة مرجع. تذكر أن الفئة "0" هي الفئة الشرعية والفئة "1" هي الفئة الاحتيالية.
from sklearn.dummy import DummyClassifier
always_accept_policy = DummyClassifier(strategy="constant", constant=0)
always_accept_policy.fit(data_train, target_train)
benefit = business_scorer(
always_accept_policy, data_test, target_test, amount=amount_test
)
print(f"فائدة سياسة 'قبول دائمًا': {benefit:,.2f} يورو")
فائدة سياسة 'قبول دائمًا': 221,445.07 يورو
ستحقق السياسة التي تعتبر جميع المعاملات شرعية ربحًا قدره حوالي 220.000 يورو. نجري نفس التقييم لمصنف يتوقع جميع المعاملات على أنها احتيالية.
always_reject_policy = DummyClassifier(strategy="constant", constant=1)
always_reject_policy.fit(data_train, target_train)
benefit = business_scorer(
always_reject_policy, data_test, target_test, amount=amount_test
)
print(f"فائدة سياسة 'رفض دائمًا': {benefit:,.2f} يورو")
فائدة سياسة 'رفض دائمًا': -698,490.00 يورو
ستؤدي مثل هذه السياسة إلى خسارة فادحة: حوالي 670.000 يورو. هذا متوقع لأن الغالبية العظمى من المعاملات شرعية وسترفضها السياسة بتكلفة غير تافهة.
من الناحية المثالية، سيسمح لنا نموذج التنبؤ الذي يقوم بتكييف قرارات القبول / الرفض على أساس كل معاملة بتحقيق ربح أكبر من 220.000 يورو من أفضل سياسات خط الأساس الثابتة لدينا.
نبدأ بنموذج انحدار لوجستي مع عتبة القرار الافتراضية
عند 0.5. هنا نقوم بضبط المعلمة الفائقة C للانحدار اللوجستي بقاعدة
تسجيل مناسبة (خسارة السجل) لضمان أن تنبؤات النموذج الاحتمالية
التي يتم إرجاعها بواسطة أسلوب predict_proba الخاص به دقيقة قدر
الإمكان، بغض النظر عن اختيار قيمة عتبة القرار.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
logistic_regression = make_pipeline(StandardScaler(), LogisticRegression())
param_grid = {"logisticregression__C": np.logspace(-6, 6, 13)}
model = GridSearchCV(logistic_regression, param_grid, scoring="neg_log_loss").fit(
data_train, target_train
)
model
print(
"فائدة الانحدار اللوجستي مع العتبة الافتراضية: "
f"{business_scorer(model, data_test, target_test, amount=amount_test):,.2f} يورو"
)
فائدة الانحدار اللوجستي مع العتبة الافتراضية: 244,919.87 يورو
يُظهر مقياس الأعمال أن نموذج التنبؤ الخاص بنا مع عتبة القرار الافتراضية يفوز بالفعل على خط الأساس من حيث الربح، وسيكون من المفيد بالفعل استخدامه لقبول أو رفض المعاملات بدلاً من قبول جميع المعاملات.
ضبط عتبة القرار#
السؤال الآن هو: هل نموذجنا هو الأمثل لنوع القرار الذي نريد اتخاذه؟
حتى الآن، لم نقم بتحسين عتبة القرار. نستخدم
TunedThresholdClassifierCV لتحسين القرار
نظرًا لمسجل أعمالنا. لتجنب التحقق المتقاطع المتداخل، سنستخدم أفضل
مقدر تم العثور عليه أثناء بحث الشبكة السابق.
tuned_model = TunedThresholdClassifierCV(
estimator=model.best_estimator_,
scoring=business_scorer,
thresholds=100,
n_jobs=2,
)
نظرًا لأن مسجل أعمالنا يتطلب مقدار كل معاملة، فإننا نحتاج إلى تمرير
هذه المعلومات في أسلوب fit. TunedThresholdClassifierCV
مسؤول عن إرسال هذه البيانات الوصفية تلقائيًا إلى المسجل الأساسي.
tuned_model.fit(data_train, target_train, amount=amount_train)
نلاحظ أن عتبة القرار المضبوطة بعيدة عن 0.5 الافتراضية:
print(f"عتبة القرار المضبوطة: {tuned_model.best_threshold_:.2f}")
عتبة القرار المضبوطة: 0.03
print(
"فائدة الانحدار اللوجستي مع عتبة مضبوطة: "
f"{business_scorer(tuned_model, data_test, target_test, amount=amount_test):,.2f} يورو"
)
فائدة الانحدار اللوجستي مع عتبة مضبوطة: 249,433.39 يورو
نلاحظ أن ضبط عتبة القرار يزيد من الربح المتوقع عند نشر نموذجنا - كما هو موضح بواسطة مقياس الأعمال. لذلك من المفيد، كلما أمكن، تحسين عتبة القرار فيما يتعلق بمقياس الأعمال.
تعيين عتبة القرار يدويًا بدلاً من ضبطها#
في المثال السابق، استخدمنا
TunedThresholdClassifierCV للعثور على عتبة
القرار المثلى. ومع ذلك، في بعض الحالات، قد يكون لدينا بعض المعرفة المسبقة
بالمشكلة المطروحة وقد نكون سعداء بتعيين عتبة القرار يدويًا.
تسمح لنا الفئة FixedThresholdClassifier بتعيين
عتبة القرار يدويًا. في وقت التنبؤ، يتصرف كنموذج مضبوط سابق، ولكن لا يتم
إجراء بحث أثناء عملية الملاءمة. لاحظ أننا هنا نستخدم
FrozenEstimator لتغليف نموذج التنبؤ
لتجنب أي إعادة ملاءمة.
هنا، سنعيد استخدام عتبة القرار الموجودة في القسم السابق لإنشاء نموذج جديد والتحقق من أنه يعطي نفس النتائج.
from sklearn.model_selection import FixedThresholdClassifier
model_fixed_threshold = FixedThresholdClassifier(
estimator=model, threshold=tuned_model.best_threshold_, prefit=True
).fit(data_train, target_train)
business_score = business_scorer(
model_fixed_threshold, data_test, target_test, amount=amount_test
)
print(f"فوائد الانحدار اللوجستي مع عتبة مضبوطة : {business_score:,.2f}€")
فوائد الانحدار اللوجستي مع عتبة مضبوطة : 249,433.39€
نلاحظ أننا حصلنا على نفس النتائج بالضبط ولكن عملية الملاءمة كانت أسرع بكثير لأننا لم نقم بأي بحث عن المعلمات الفائقة.
أخيرًا، قد يكون تقدير مقياس الأعمال (المتوسط) نفسه غير موثوق، لا سيما عندما يكون عدد نقاط البيانات في فئة الأقلية صغيرًا جدًا. يجب أن يتم تأكيد أي تأثير تجاري يقدره التحقق المتقاطع لمقياس الأعمال على البيانات التاريخية (التقييم غير المتصل) بشكل مثالي عن طريق اختبار A / B على البيانات الحية (التقييم عبر الإنترنت). لاحظ مع ذلك أن اختبار نماذج A / B خارج نطاق مكتبة scikit-learn نفسها.
Total running time of the script: (0 minutes 41.462 seconds)
Related examples
أبرز الميزات الجديدة في الإصدار 1.5 من scikit-learn