ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
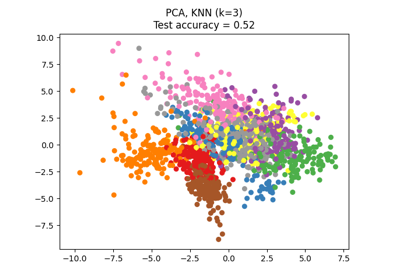
هذا مثال لرسم حدود التمييز والقطع الناقص لتشتت كل فئة، والتي تم تعلمها بواسطة LinearDiscriminantAnalysis (LDA) و QuadraticDiscriminantAnalysis (QDA). يُظهر القطع الناقص الانحراف المعياري المزدوج لكل فئة. مع LDA، يكون الانحراف المعياري هو نفسه لجميع الفئات، في حين أن لكل فئة انحرافها المعياري الخاص بها مع QDA.
# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause
توليد البيانات#
أولاً، نُعرّف دالة لتوليد بيانات صناعية. تقوم بإنشاء كتلتين مركزتين عند (0, 0) و (1, 1). يتم تعيين فئة محددة لكل كتلة. يتم التحكم في تشتت الكتلة بواسطة المعاملات cov_class_1 و cov_class_2، وهي مصفوفات التشتت المستخدمة عند توليد العينات من التوزيعات الغاوسية.
import numpy as np
def make_data(n_samples, n_features, cov_class_1, cov_class_2, seed=0):
rng = np.random.RandomState(seed)
X = np.concatenate(
[
rng.randn(n_samples, n_features) @ cov_class_1,
rng.randn(n_samples, n_features) @ cov_class_2 + np.array([1, 1]),
]
)
y = np.concatenate([np.zeros(n_samples), np.ones(n_samples)])
return X, y
نقوم بتوليد ثلاث مجموعات بيانات. في مجموعة البيانات الأولى، تشترك الفئتان في نفس مصفوفة التشتت، وتتميز هذه المصفوفة بأنها كروية (متساوية التشتت). مجموعة البيانات الثانية مماثلة للأولى ولكنها لا تفرض أن يكون التشتت كرويًا. وأخيرًا، تمتلك مجموعة البيانات الثالثة مصفوفة تشتت غير كروية لكل فئة.
covariance = np.array([[1, 0], [0, 1]])
X_isotropic_covariance, y_isotropic_covariance = make_data(
n_samples=1_000,
n_features=2,
cov_class_1=covariance,
cov_class_2=covariance,
seed=0,
)
covariance = np.array([[0.0, -0.23], [0.83, 0.23]])
X_shared_covariance, y_shared_covariance = make_data(
n_samples=300,
n_features=2,
cov_class_1=covariance,
cov_class_2=covariance,
seed=0,
)
cov_class_1 = np.array([[0.0, -1.0], [2.5, 0.7]]) * 2.0
cov_class_2 = cov_class_1.T
X_different_covariance, y_different_covariance = make_data(
n_samples=300,
n_features=2,
cov_class_1=cov_class_1,
cov_class_2=cov_class_2,
seed=0,
)
دالات الرسم#
يستخدم الكود أدناه لرسم عدة معلومات من المقدرات المستخدمة، أي LinearDiscriminantAnalysis (LDA) و QuadraticDiscriminantAnalysis (QDA). وتشمل المعلومات المعروضة:
حدود التمييز بناءً على تقدير احتمالية المقدر؛
رسم متفرق مع دوائر تمثل العينات المصنفة بشكل صحيح؛
رسم متفرق مع علامات الصليب التي تمثل العينات المصنفة بشكل خاطئ؛
متوسط كل فئة، المقدر بواسطة المقدر، مع علامة نجمية؛
التشتت المقدر الممثل بقطع ناقص عند انحرافين معياريين من المتوسط.
import matplotlib as mpl
from matplotlib import colors
from sklearn.inspection import DecisionBoundaryDisplay
def plot_ellipse(mean, cov, color, ax):
v, w = np.linalg.eigh(cov)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan(u[1] / u[0])
angle = 180 * angle / np.pi # التحويل إلى درجات
# Gaussian مملوء عند انحرافين معياريين
ell = mpl.patches.Ellipse(
mean,
2 * v[0] ** 0.5,
2 * v[1] ** 0.5,
angle=180 + angle,
facecolor=color,
edgecolor="black",
linewidth=2,
)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.4)
ax.add_artist(ell)
def plot_result(estimator, X, y, ax):
cmap = colors.ListedColormap(["tab:red", "tab:blue"])
DecisionBoundaryDisplay.from_estimator(
estimator,
X,
response_method="predict_proba",
plot_method="pcolormesh",
ax=ax,
cmap="RdBu",
alpha=0.3,
)
DecisionBoundaryDisplay.from_estimator(
estimator,
X,
response_method="predict_proba",
plot_method="contour",
ax=ax,
alpha=1.0,
levels=[0.5],
)
y_pred = estimator.predict(X)
X_right, y_right = X[y == y_pred], y[y == y_pred]
X_wrong, y_wrong = X[y != y_pred], y[y != y_pred]
ax.scatter(X_right[:, 0], X_right[:, 1], c=y_right, s=20, cmap=cmap, alpha=0.5)
ax.scatter(
X_wrong[:, 0],
X_wrong[:, 1],
c=y_wrong,
s=30,
cmap=cmap,
alpha=0.9,
marker="x",
)
ax.scatter(
estimator.means_[:, 0],
estimator.means_[:, 1],
c="yellow",
s=200,
marker="*",
edgecolor="black",
)
if isinstance(estimator, LinearDiscriminantAnalysis):
covariance = [estimator.covariance_] * 2
else:
covariance = estimator.covariance_
plot_ellipse(estimator.means_[0], covariance[0], "tab:red", ax)
plot_ellipse(estimator.means_[1], covariance[1], "tab:blue", ax)
ax.set_box_aspect(1)
ax.spines["top"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.set(xticks=[], yticks=[])
مقارنة LDA و QDA#
نقارن بين المقدرين LDA و QDA على جميع مجموعات البيانات الثلاث.
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import (
LinearDiscriminantAnalysis,
QuadraticDiscriminantAnalysis,
)
fig, axs = plt.subplots(nrows=3, ncols=2, sharex="row", sharey="row", figsize=(8, 12))
lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
qda = QuadraticDiscriminantAnalysis(store_covariance=True)
for ax_row, X, y in zip(
axs,
(X_isotropic_covariance, X_shared_covariance, X_different_covariance),
(y_isotropic_covariance, y_shared_covariance, y_different_covariance),
):
lda.fit(X, y)
plot_result(lda, X, y, ax_row[0])
qda.fit(X, y)
plot_result(qda, X, y, ax_row[1])
axs[0, 0].set_title("Linear Discriminant Analysis")
axs[0, 0].set_ylabel("Data with fixed and spherical covariance")
axs[1, 0].set_ylabel("Data with fixed covariance")
axs[0, 1].set_title("Quadratic Discriminant Analysis")
axs[2, 0].set_ylabel("Data with varying covariances")
fig.suptitle(
"Linear Discriminant Analysis vs Quadratic Discriminant Analysis",
y=0.94,
fontsize=15,
)
plt.show()
أول شيء مهم يجب ملاحظته هو أن LDA و QDA متكافئان بالنسبة لمجموعتي البيانات الأولى والثانية. في الواقع، الاختلاف الرئيسي هو أن LDA يفترض أن مصفوفة التشتت لكل فئة متساوية، في حين أن QDA يقدر مصفوفة تشتت لكل فئة. بما أن عملية توليد البيانات في هذه الحالات لها نفس مصفوفة التشتت لكلتا الفئتين، فإن QDA يقدر مصفوفتي تشتت متساويتين (تقريبًا) وبالتالي متكافئتين مع مصفوفة التشتت المقدرة بواسطة LDA.
في مجموعة البيانات الأولى، تكون مصفوفة التشتت المستخدمة لتوليد مجموعة البيانات كروية، مما يؤدي إلى حدود تمييز تتطابق مع القاطع العمودي بين المتوسطين. لم يعد هذا هو الحال بالنسبة لمجموعة البيانات الثانية. تمر حدود التمييز فقط عبر منتصف المتوسطين.
وأخيرًا، في مجموعة البيانات الثالثة، نلاحظ الاختلاف الحقيقي بين LDA و QDA. يقوم QDA بضبط مصفوفتي تشتت ويوفر حدود تمييز غير خطية، في حين أن LDA لا يضبط بشكل صحيح لأنه يفترض أن كلا الفئتين تشتركان في مصفوفة تشتت واحدة.
Total running time of the script: (0 minutes 0.458 seconds)
Related examples
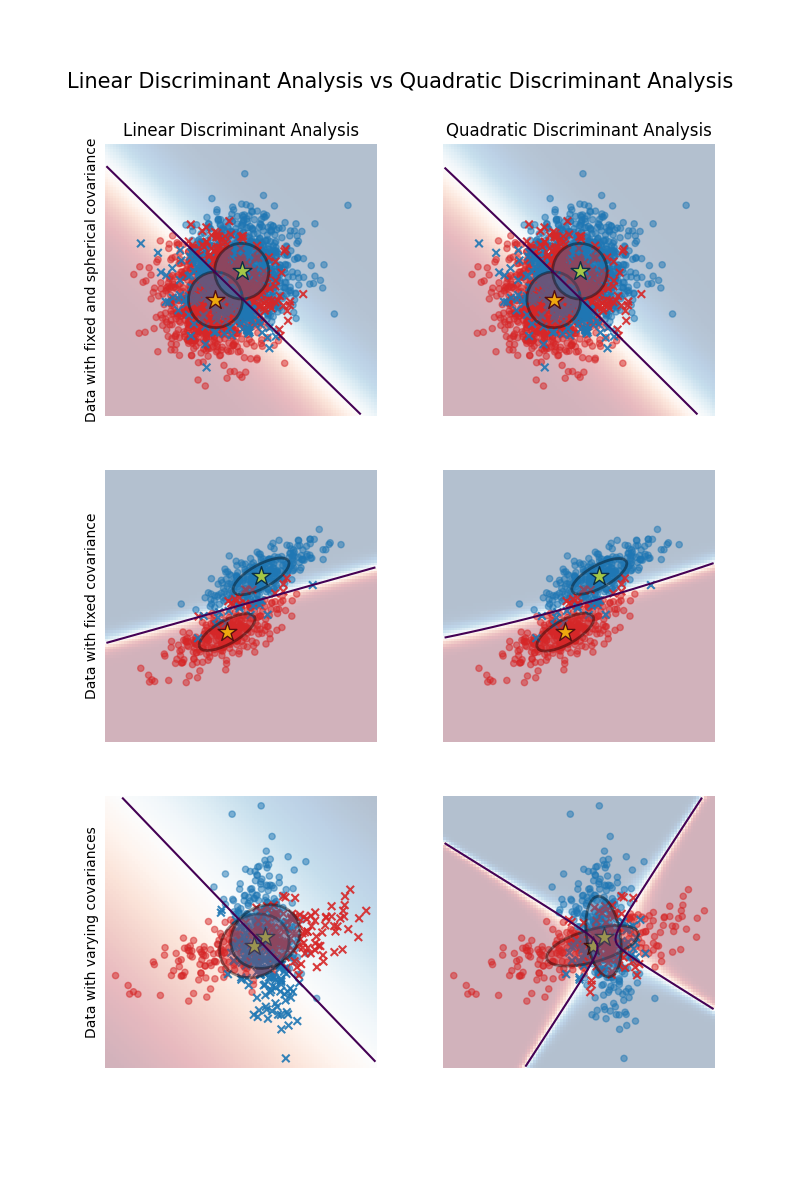
Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification
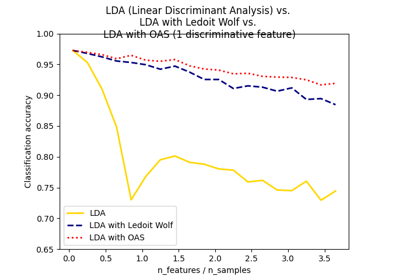
مقارنة بين الإسقاط ثنائي الأبعاد للمجموعة البيانات آيريس باستخدام LDA وPCA
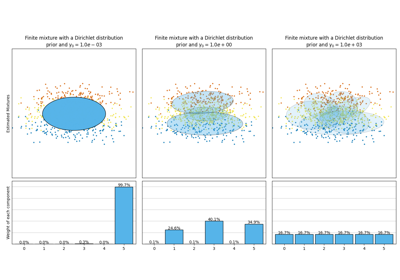
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر