ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

عرض توضيحي لخوارزمية التجميع HDBSCAN#

في هذا العرض التوضيحي، سنلقي نظرة على cluster.HDBSCAN من منظور تعميم خوارزمية cluster.DBSCAN. سنقارن بين الخوارزميتين على مجموعات بيانات محددة. وأخيرًا، سنقيم حساسية HDBSCAN تجاه بعض المعاملات.

نحن نحدد أولاً بعض وظائف المنفعة للراحة.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import DBSCAN, HDBSCAN
from sklearn.datasets import make_blobs


def plot(X, labels, probabilities=None, parameters=None, ground_truth=False, ax=None):
    if ax is None:
        _, ax = plt.subplots(figsize=(10, 4))
    labels = labels if labels is not None else np.ones(X.shape[0])
    probabilities = probabilities if probabilities is not None else np.ones(X.shape[0])
    # Black removed and is used for noise instead.
    unique_labels = set(labels)
    colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
    # The probability of a point belonging to its labeled cluster determines
    # the size of its marker
    proba_map = {idx: probabilities[idx] for idx in range(len(labels))}
    for k, col in zip(unique_labels, colors):
        if k == -1:
            # Black used for noise.
            col = [0, 0, 0, 1]

        class_index = np.where(labels == k)[0]
        for ci in class_index:
            ax.plot(
                X[ci, 0],
                X[ci, 1],
                "x" if k == -1 else "o",
                markerfacecolor=tuple(col),
                markeredgecolor="k",
                markersize=4 if k == -1 else 1 + 5 * proba_map[ci],
            )
    n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
    preamble = "True" if ground_truth else "Estimated"
    title = f"{preamble} number of clusters: {n_clusters_}"
    if parameters is not None:
        parameters_str = ", ".join(f"{k}={v}" for k, v in parameters.items())
        title += f" | {parameters_str}"
    ax.set_title(title)
    plt.tight_layout()

توليد بيانات العينة#

إحدى المزايا العظيمة لـ HDBSCAN على DBSCAN هي متانتها الجاهزة للاستخدام. إنها ملحوظة بشكل خاص على الخلطات غير المتجانسة للبيانات. مثل DBSCAN، يمكنها نمذجة أشكال وتوزيعات عشوائية، ومع ذلك، على عكس DBSCAN، لا تتطلب تحديد معامل حساس eps.

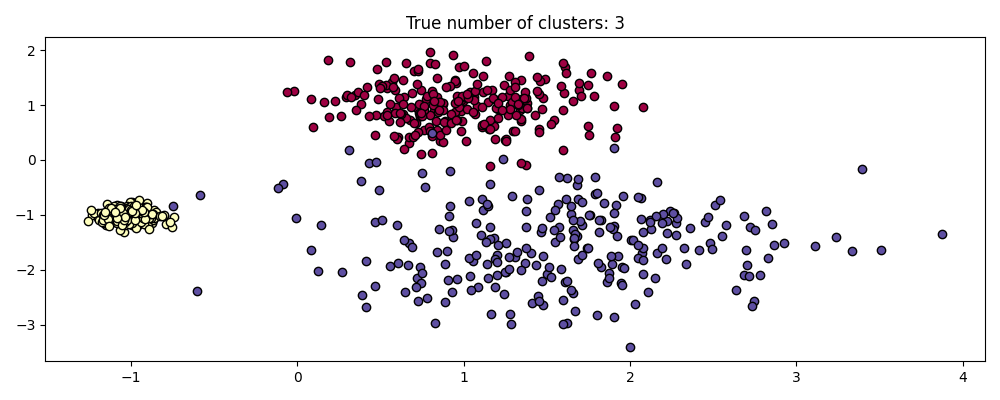
على سبيل المثال، أدناه، نولد مجموعة بيانات من مزيج من ثلاثة توزيعات غاوسية ثنائية الأبعاد ومتساوية.

centers = [[1, 1], [-1, -1], [1.5, -1.5]]
X, labels_true = make_blobs(
    n_samples=750, centers=centers, cluster_std=[0.4, 0.1, 0.75], random_state=0
)
plot(X, labels=labels_true, ground_truth=True)

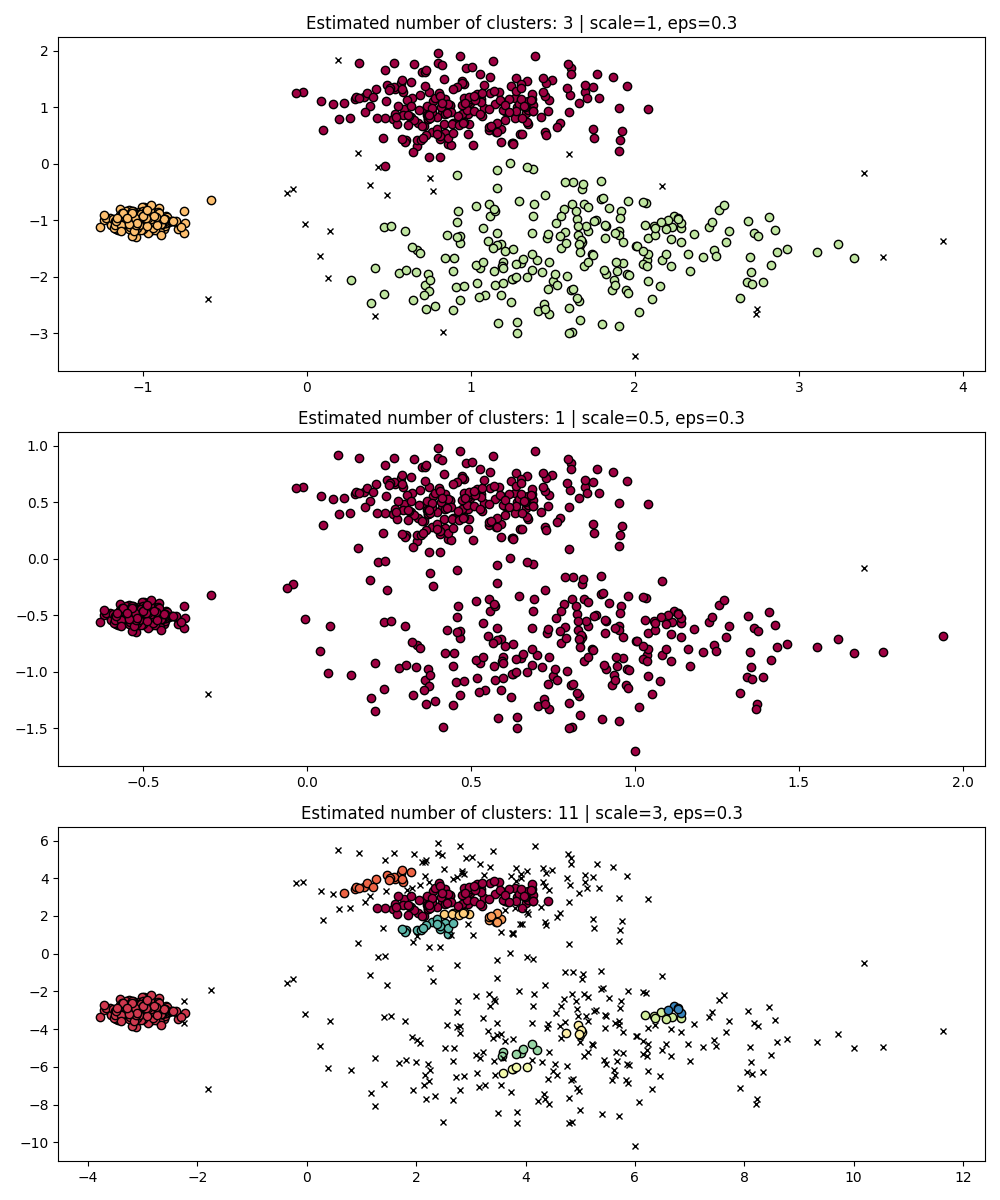
عدم التغير في المقياس#

من الجدير بالذكر أنه، في حين أن DBSCAN يوفر قيمة افتراضية لمعامل eps، إلا أنه لا يمتلك قيمة افتراضية مناسبة ويجب ضبطه لمجموعة البيانات المحددة قيد الاستخدام.

كمثال بسيط، ضع في اعتبارك التجميع لمعامل eps مضبوط لمجموعة بيانات واحدة، والتجميع الذي تم الحصول عليه بنفس القيمة ولكن تم تطبيقه على إصدارات مقياسها من مجموعة البيانات.

fig, axes = plt.subplots(3, 1, figsize=(10, 12))
dbs = DBSCAN(eps=0.3)
for idx, scale in enumerate([1, 0.5, 3]):
    dbs.fit(X * scale)
    plot(X * scale, dbs.labels_, parameters={"scale": scale, "eps": 0.3}, ax=axes[idx])

Estimated number of clusters: 3 | scale=1, eps=0.3, Estimated number of clusters: 1 | scale=0.5, eps=0.3, Estimated number of clusters: 11 | scale=3, eps=0.3

في الواقع، من أجل الحفاظ على نفس النتائج، سيتعين علينا ضبط eps بنفس العامل.

fig, axis = plt.subplots(1, 1, figsize=(12, 5))
dbs = DBSCAN(eps=0.9).fit(3 * X)
plot(3 * X, dbs.labels_, parameters={"scale": 3, "eps": 0.9}, ax=axis)

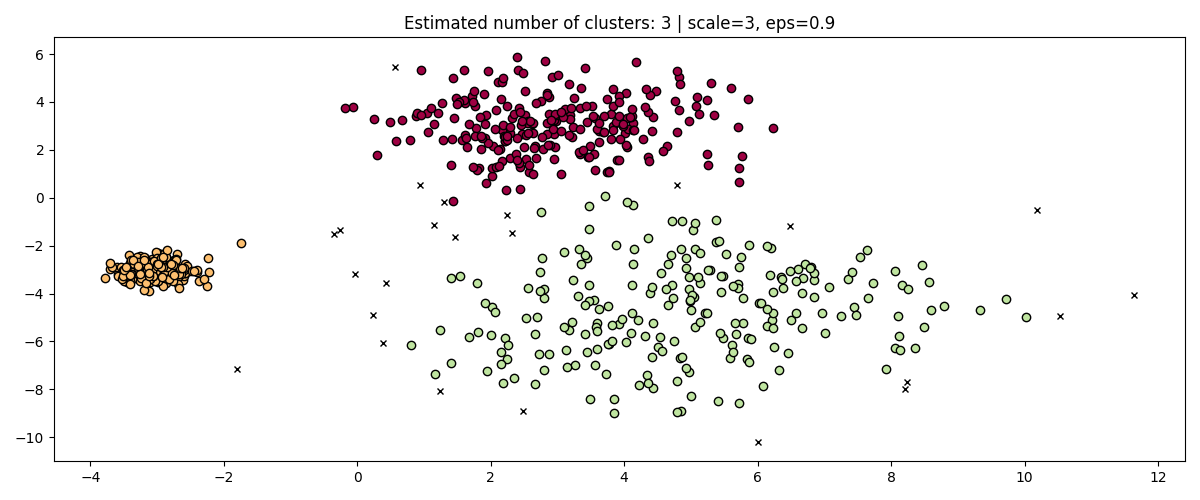
Estimated number of clusters: 3 | scale=3, eps=0.9

في حين أن توحيد البيانات (على سبيل المثال باستخدام sklearn.preprocessing.StandardScaler) يساعد في التخفيف من هذه المشكلة، يجب توخي الحذر الشديد لاختيار القيمة المناسبة لـ eps.

HDBSCAN أكثر متانة في هذا المعنى: يمكن اعتبار HDBSCAN التجميع على جميع القيم الممكنة لـ eps واستخراج أفضل التجمعات من جميع التجمعات الممكنة (انظر: ref:User Guide <HDBSCAN>). إحدى المزايا الفورية هي أن HDBSCAN غير متغير في المقياس.

fig, axes = plt.subplots(3, 1, figsize=(10, 12))
hdb = HDBSCAN()
for idx, scale in enumerate([1, 0.5, 3]):
    hdb.fit(X * scale)
    plot(
        X * scale,
        hdb.labels_,
        hdb.probabilities_,
        ax=axes[idx],
        parameters={"scale": scale},
    )

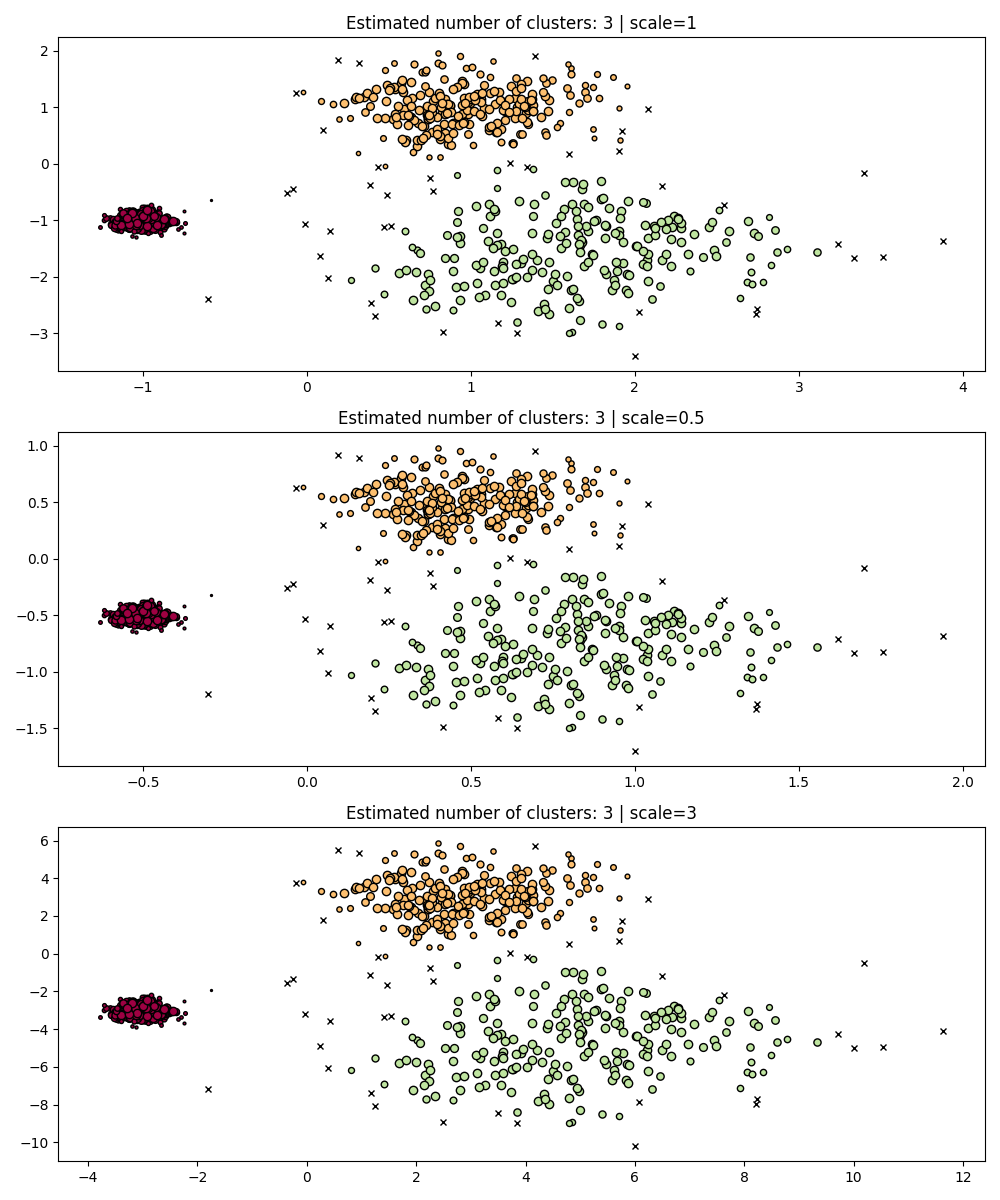
Estimated number of clusters: 3 | scale=1, Estimated number of clusters: 3 | scale=0.5, Estimated number of clusters: 3 | scale=3

التجميع متعدد المقاييس#

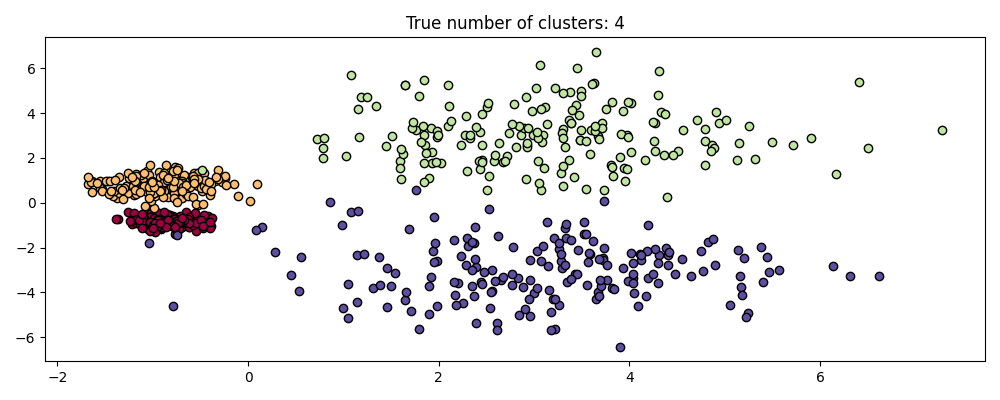
HDBSCAN أكثر من مجرد عدم التغير في المقياس - فهو قادر على التجميع متعدد المقاييس، والذي يحسب حساب التجمعات ذات الكثافة المتغيرة. يفترض DBSCAN التقليدي أن أي تجمعات محتملة متجانسة في الكثافة. HDBSCAN خالي من مثل هذه القيود. لتوضيح ذلك، نأخذ في الاعتبار مجموعة البيانات التالية

centers = [[-0.85, -0.85], [-0.85, 0.85], [3, 3], [3, -3]]
X, labels_true = make_blobs(
    n_samples=750, centers=centers, cluster_std=[0.2, 0.35, 1.35, 1.35], random_state=0
)
plot(X, labels=labels_true, ground_truth=True)

هذه المجموعة أكثر صعوبة بالنسبة لـ DBSCAN بسبب الكثافة المتغيرة والانفصال المكاني:

إذا كان eps كبيرًا جدًا، فإننا نخاطر بتجميع التجمعات الكثيفة بشكل خاطئ كمجموعة واحدة نظرًا لأن قابلية الوصول المتبادل لها ستوسع

التجمعات. - إذا كان eps صغيرًا جدًا، فإننا نخاطر بتجزئة التجمعات النادرة إلى العديد من التجمعات الخاطئة.

ناهيك عن أن هذا يتطلب خيارات ضبط يدوية لـ eps حتى نجد حل وسط نشعر بالراحة معه.

fig, axes = plt.subplots(2, 1, figsize=(10, 8))
params = {"eps": 0.7}
dbs = DBSCAN(**params).fit(X)
plot(X, dbs.labels_, parameters=params, ax=axes[0])
params = {"eps": 0.3}
dbs = DBSCAN(**params).fit(X)
plot(X, dbs.labels_, parameters=params, ax=axes[1])

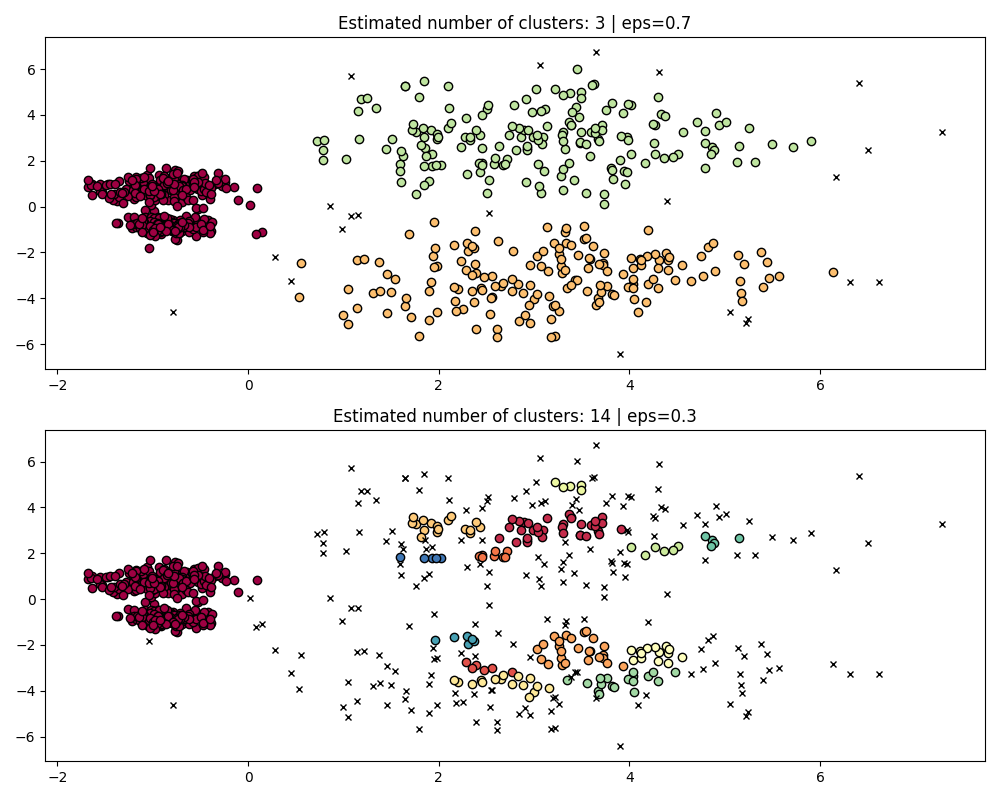
Estimated number of clusters: 3 | eps=0.7, Estimated number of clusters: 14 | eps=0.3

لتجزئة التجمعات الكثيفة بشكل صحيح، سنحتاج إلى قيمة أصغر من إبسيلون، ومع ذلك، في eps=0.3، فإننا بالفعل نجزئ التجمعات النادرة، والتي ستصبح أكثر حدة مع تقليل إبسيلون. في الواقع يبدو أن DBSCAN غير قادر على فصل التجمعات الكثيفة في نفس الوقت أثناء منع التجمعات النادرة من التجزئة. دعنا نقارن مع HDBSCAN.

hdb = HDBSCAN().fit(X)
plot(X, hdb.labels_, hdb.probabilities_)

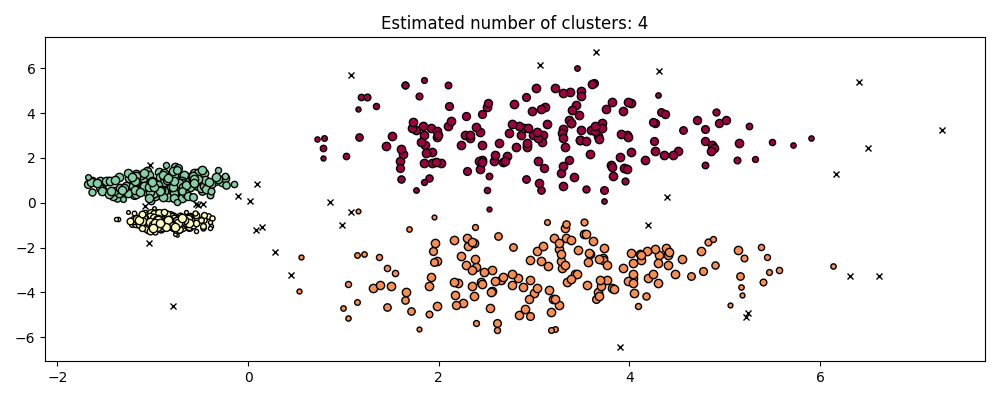
HDBSCAN قادر على التكيف مع البنية متعددة المقاييس لمجموعة البيانات دون تتطلب ضبط المعاملات. في حين أن أي مجموعة بيانات مثيرة للاهتمام بما فيه الكفاية سيتطلب الضبط، توضح هذه الحالة أن HDBSCAN يمكن أن يؤدي إلى نوعية أفضل فئات التجميع دون تدخل المستخدم والتي لا يمكن الوصول إليها عبر DBSCAN. %% متانة المعاملات ------------------------- في النهاية، سيكون الضبط خطوة مهمة في أي تطبيق في العالم الحقيقي، لذلك دعنا نلقي نظرة على بعض المعاملات الأكثر أهمية لـ HDBSCAN. في حين أن HDBSCAN خالٍ من معامل eps لـ DBSCAN، فإنه لا يزال يحتوي على بعض المعاملات مثل min_cluster_size و min_samples التي تضبط نتائجه فيما يتعلق بالكثافة. ومع ذلك، سنرى أن HDBSCAN متين نسبيًا لمختلف الأمثلة الواقعية بفضل هذه المعاملات التي يساعد معناها الواضح في ضبطها.

`min_cluster_size`#

min_cluster_size هو الحد الأدنى لعدد العينات في مجموعة لكي تعتبر المجموعة مجموعة.

ستترك التجمعات الأصغر من هذه الحجم كضجيج. القيمة الافتراضية هي 5. يتم ضبط هذا المعامل بشكل عام على قيم أكبر حسب الحاجة. من المرجح أن تؤدي القيم الأصغر إلى نتائج مع عدد أقل من النقاط المسماة كضجيج. ومع ذلك، فإن القيم الصغيرة جدًا ستؤدي إلى اختيار التجمعات الفرعية الخاطئة وتفضيلها. تميل القيم الأكبر إلى أن تكون أكثر متانة فيما يتعلق بمجموعات البيانات الضجيج، على سبيل المثال، التجمعات عالية التباين مع تداخل كبير.

PARAM = ({"min_cluster_size": 5}, {"min_cluster_size": 3}, {"min_cluster_size": 25})
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    hdb = HDBSCAN(**param).fit(X)
    labels = hdb.labels_

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])

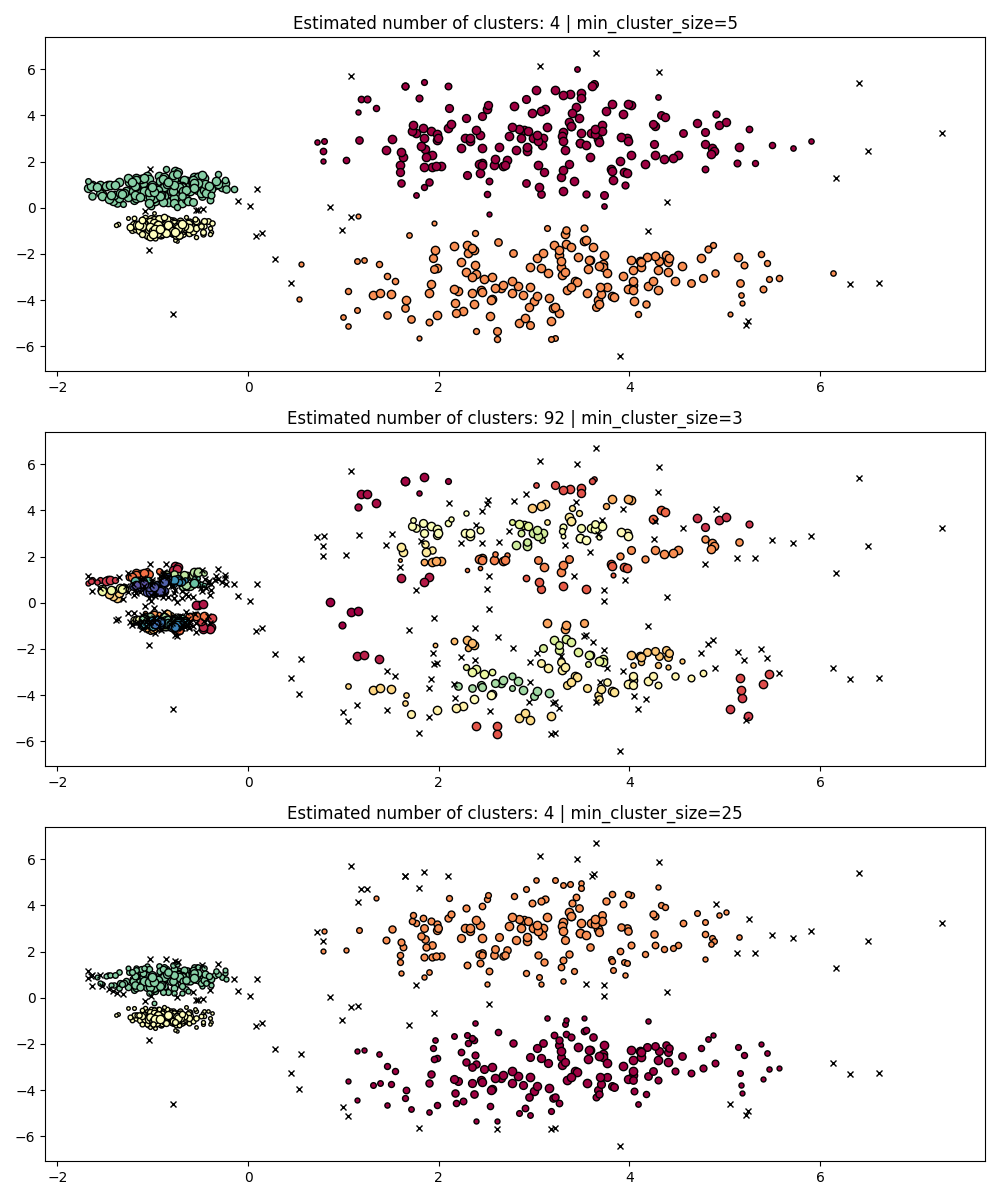
Estimated number of clusters: 4 | min_cluster_size=5, Estimated number of clusters: 92 | min_cluster_size=3, Estimated number of clusters: 4 | min_cluster_size=25

`min_samples`#

min_samples هو عدد العينات في حي لكي تعتبر النقطة نقطة أساسية، بما في ذلك النقطة نفسها. min_samples الافتراضي إلى min_cluster_size. على غرار min_cluster_size، تزيد القيم الأكبر لـ min_samples من متانة النموذج للضجيج، ولكنها تخاطر بتجاهل أو تجاهل التجمعات المحتملة الصالحة ولكن الصغيرة. من الأفضل ضبط min_samples بعد العثور على قيمة جيدة لـ min_cluster_size.

PARAM = (
    {"min_cluster_size": 20, "min_samples": 5},
    {"min_cluster_size": 20, "min_samples": 3},
    {"min_cluster_size": 20, "min_samples": 25},
)
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    hdb = HDBSCAN(**param).fit(X)
    labels = hdb.labels_

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])

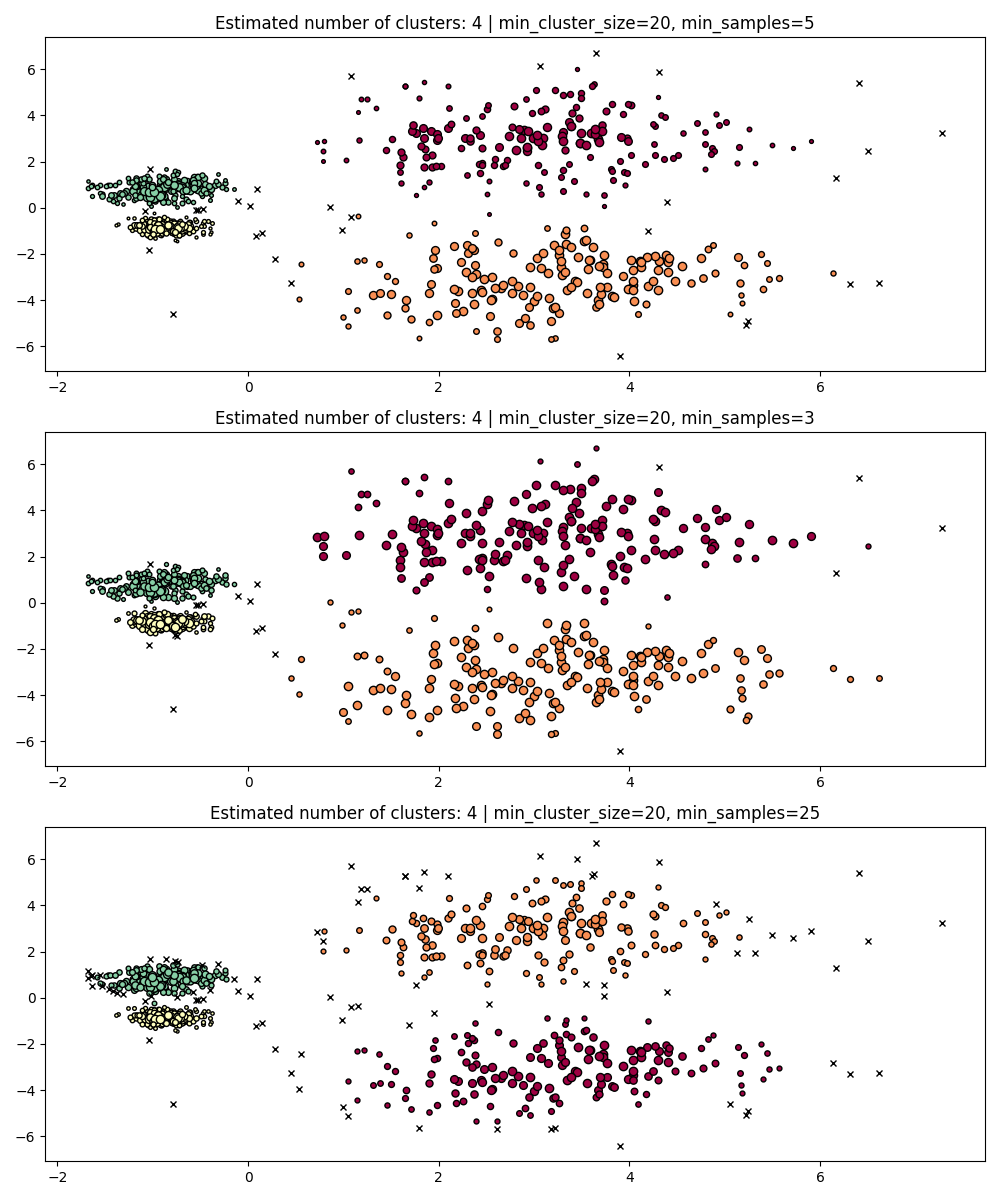
Estimated number of clusters: 4 | min_cluster_size=20, min_samples=5, Estimated number of clusters: 4 | min_cluster_size=20, min_samples=3, Estimated number of clusters: 4 | min_cluster_size=20, min_samples=25

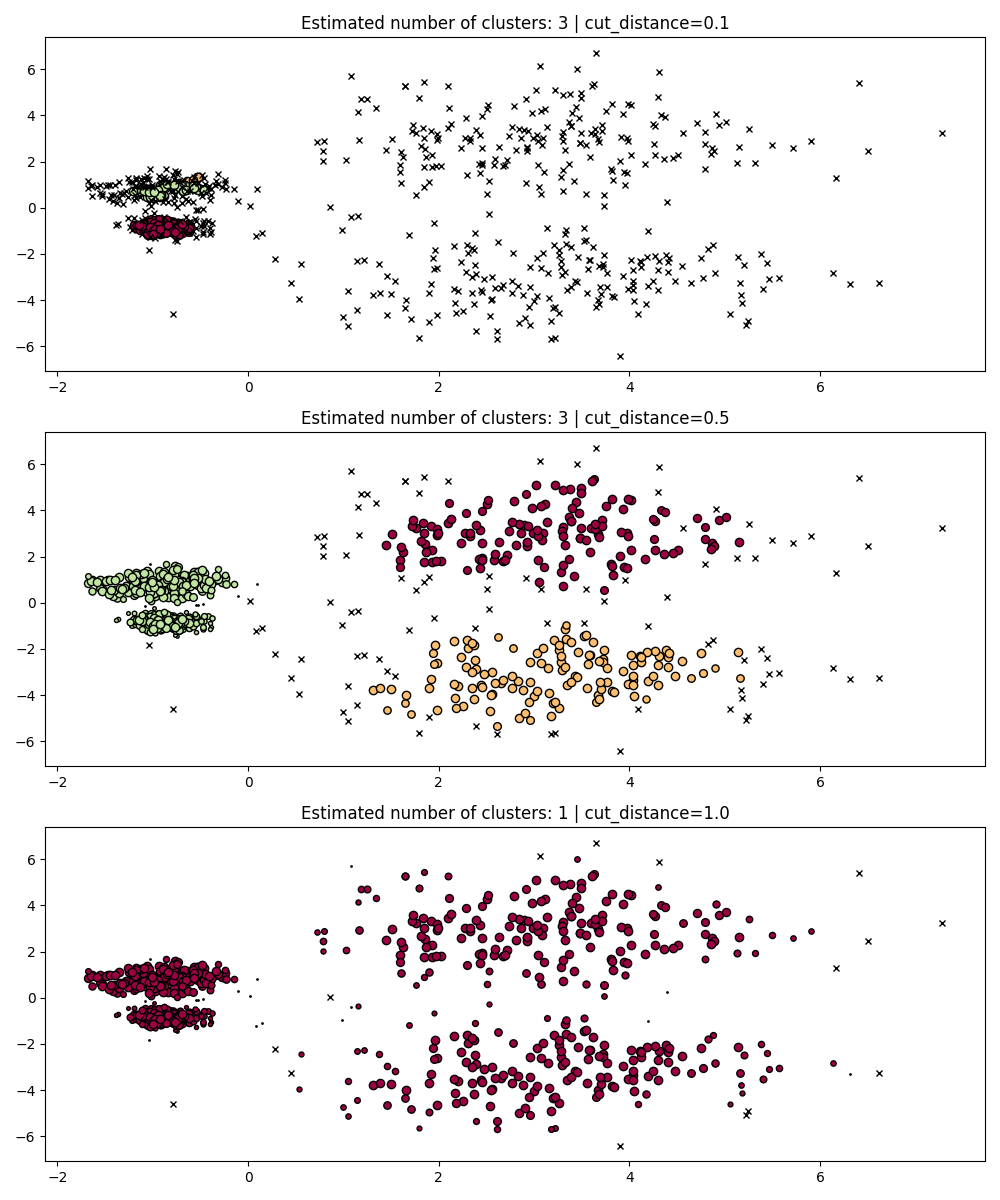
`dbscan_clustering`#

أثناء fit، يقوم HDBSCAN ببناء شجرة ارتباط واحدة والتي تشفر تجميع جميع النقاط عبر جميع القيم لـ DBSCAN's معامل eps. يمكننا بالتالي رسم وتقييم هذه التجميعات بكفاءة دون إعادة حساب كاملة القيم الوسيطة مثل المسافات الأساسية، والقابلية للوصول المتبادلة، وشجرة الإمتداد الدنيا. كل ما نحتاج إلى فعله هو تحديد cut_distance (المعادل لـ eps) نريد التجميع معه.

PARAM = (
    {"cut_distance": 0.1},
    {"cut_distance": 0.5},
    {"cut_distance": 1.0},
)
hdb = HDBSCAN()
hdb.fit(X)
fig, axes = plt.subplots(len(PARAM), 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    labels = hdb.dbscan_clustering(**param)

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])