ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

تغيير معامل التنظيم في الشبكة العصبية متعددة الطبقات#

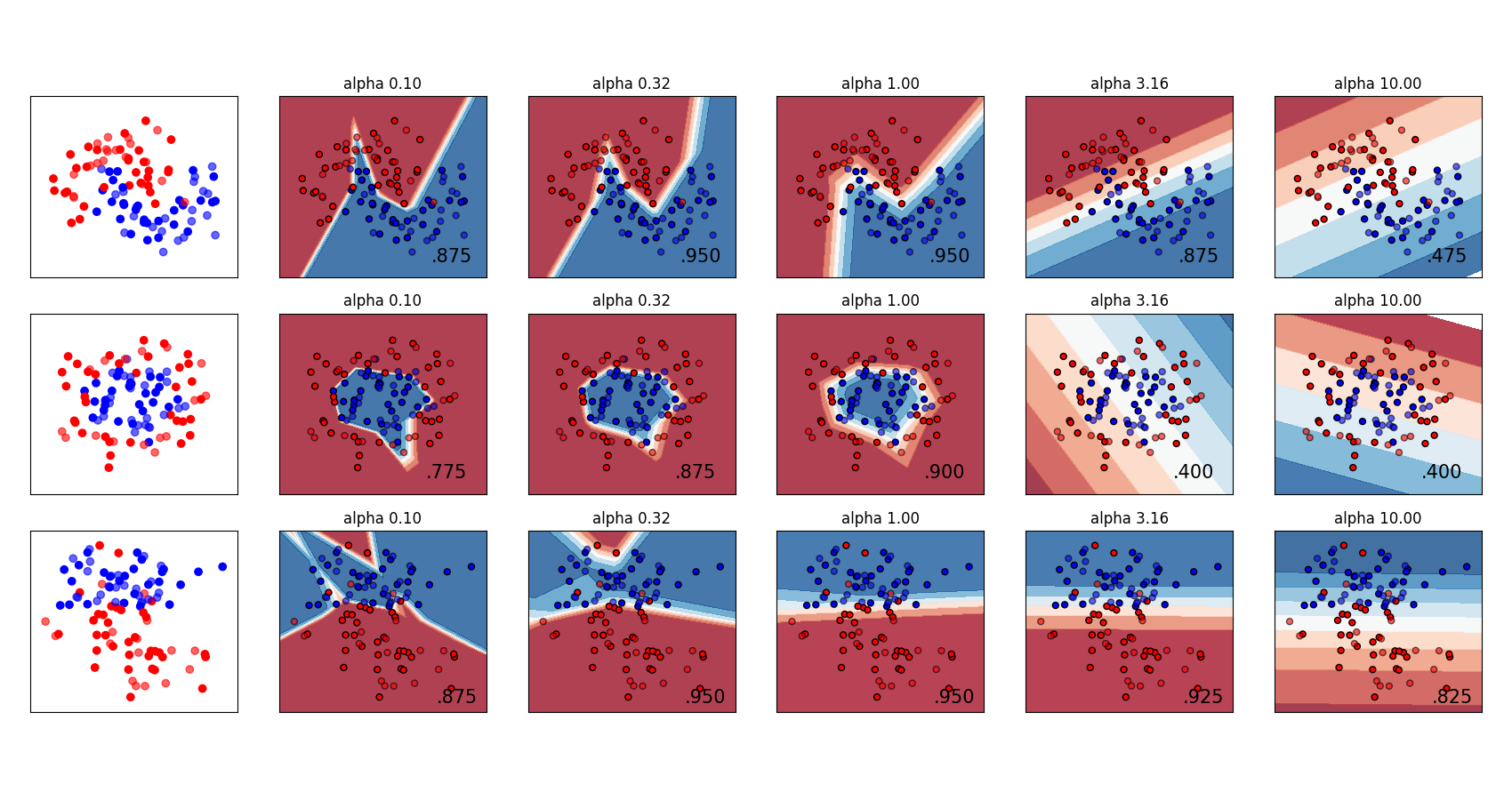
مقارنة بين قيم مختلفة لمعامل التنظيم 'alpha' على مجموعات بيانات اصطناعية. يوضح الرسم البياني أن قيم alpha المختلفة تعطي وظائف قرار مختلفة.

Alpha هو معامل لمصطلح التنظيم، المعروف أيضًا باسم مصطلح العقوبة، والذي يحارب الإفراط في التحديد من خلال تقييد حجم الأوزان. قد يؤدي زيادة alpha إلى إصلاح التباين العالي (وهو علامة على الإفراط في التحديد) من خلال تشجيع الأوزان الأصغر، مما ينتج عنها رسم بياني لحدود القرار يظهر بانحناءات أقل. وبالمثل، قد يؤدي تقليل alpha إلى إصلاح الانحياز العالي (وهو علامة على عدم التحديد الكافي) من خلال تشجيع الأوزان الأكبر، مما قد يؤدي إلى حدود قرار أكثر تعقيدًا.

alpha 0.10, alpha 0.32, alpha 1.00, alpha 3.16, alpha 10.00, alpha 0.10, alpha 0.32, alpha 1.00, alpha 3.16, alpha 10.00, alpha 0.10, alpha 0.32, alpha 1.00, alpha 3.16, alpha 10.00

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap

from sklearn.datasets import make_circles, make_classification, make_moons
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

h = 0.02  # حجم الخطوة في الشبكة

alphas = np.logspace(-1, 1, 5)

classifiers = []
names = []
for alpha in alphas:
    classifiers.append(
        make_pipeline(
            StandardScaler(),
            MLPClassifier(
                solver="lbfgs",
                alpha=alpha,
                random_state=1,
                max_iter=2000,
                early_stopping=True,
                hidden_layer_sizes=[10, 10],
            ),
        )
    )
    names.append(f"alpha {alpha:.2f}")

X, y = make_classification(
    n_features=2, n_redundant=0, n_informative=2, random_state=0, n_clusters_per_class=1
)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)

datasets = [
    make_moons(noise=0.3, random_state=0),
    make_circles(noise=0.2, factor=0.5, random_state=1),
    linearly_separable,
]

figure = plt.figure(figsize=(17, 9))
i = 1
# التكرار على مجموعات البيانات
for X, y in datasets:
    # تقسيم البيانات إلى جزء تدريب وجزء اختبار
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.4, random_state=42
    )

    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # رسم البيانات فقط في البداية
    cm = plt.cm.RdBu
    cm_bright = ListedColormap(["#FF0000", "#0000FF"])
    ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
    # رسم نقاط التدريب
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
    # ونقاط الاختبار
    ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xticks(())
    ax.set_yticks(())
    i += 1

    # التكرار على المصنفات
    for name, clf in zip(names, classifiers):
        ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
        clf.fit(X_train, y_train)
        score = clf.score(X_test, y_test)

        # رسم حدود القرار. ولذلك، سنقوم بتعيين لون لكل
        # نقطة في الشبكة [x_min, x_max] x [y_min, y_max].
        if hasattr(clf, "decision_function"):
            Z = clf.decision_function(np.column_stack([xx.ravel(), yy.ravel()]))
        else:
            Z = clf.predict_proba(np.column_stack([xx.ravel(), yy.ravel()]))[:, 1]

        # وضع النتيجة في رسم ملون
        Z = Z.reshape(xx.shape)
        ax.contourf(xx, yy, Z, cmap=cm, alpha=0.8)

        # رسم أيضًا نقاط التدريب
        ax.scatter(
            X_train[:, 0],
            X_train[:, 1],
            c=y_train,
            cmap=cm_bright,
            edgecolors="black",
            s=25,
        )
        # ونقاط الاختبار
        ax.scatter(
            X_test[:, 0],
            X_test[:, 1],
            c=y_test,
            cmap=cm_bright,
            alpha=0.6,
            edgecolors="black",
            s=25,
        )

        ax.set_xlim(xx.min(), xx.max())
        ax.set_ylim(yy.min(), yy.max())
        ax.set_xticks(())
        ax.set_yticks(())
        ax.set_title(name)
        ax.text(
            xx.max() - 0.3,
            yy.min() + 0.3,
            f"{score:.3f}".lstrip("0"),
            size=15,
            horizontalalignment="right",
        )
        i += 1

figure.subplots_adjust(left=0.02, right=0.98)
plt.show()