ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
خفض اللفافة السويسرية واللفافة السويسرية ذات الثقب#
يسعى هذا الدفتر إلى مقارنة تقنيتين شائعتين لخفض الأبعاد غير الخطية، وهما تضمين الجوار العشوائي الموزع على شكل حرف T (t-SNE) والتضمين الخطي المحلي (LLE)، على مجموعة بيانات اللفافة السويسرية الكلاسيكية. بعد ذلك، سنستكشف كيفية تعاملهما مع إضافة ثقب في البيانات.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
اللفافة السويسرية#
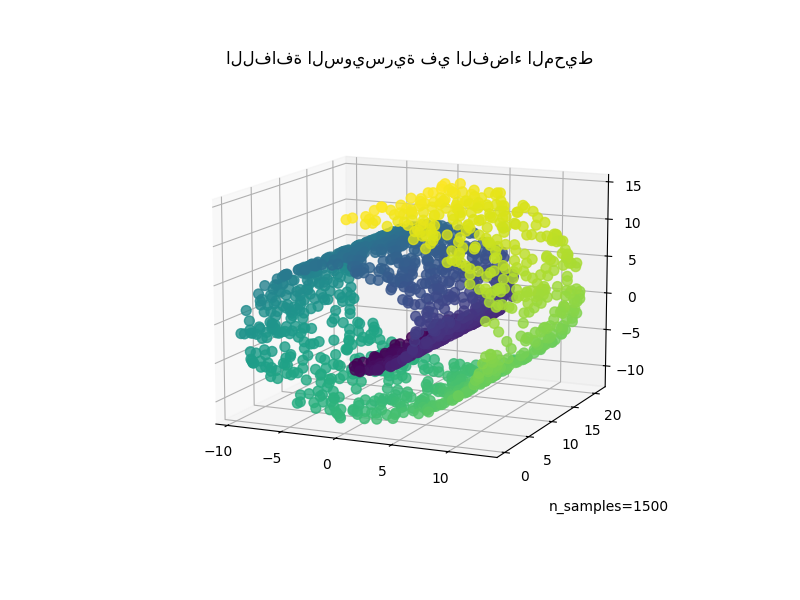
نبدأ بتوليد مجموعة بيانات اللفافة السويسرية.
import matplotlib.pyplot as plt
from sklearn import datasets, manifold
sr_points, sr_color = datasets.make_swiss_roll(n_samples=1500, random_state=0)
الآن، لنلقِ نظرة على بياناتنا:
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
sr_points[:, 0], sr_points[:, 1], sr_points[:, 2], c=sr_color, s=50, alpha=0.8
)
ax.set_title("اللفافة السويسرية في الفضاء المحيط")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)
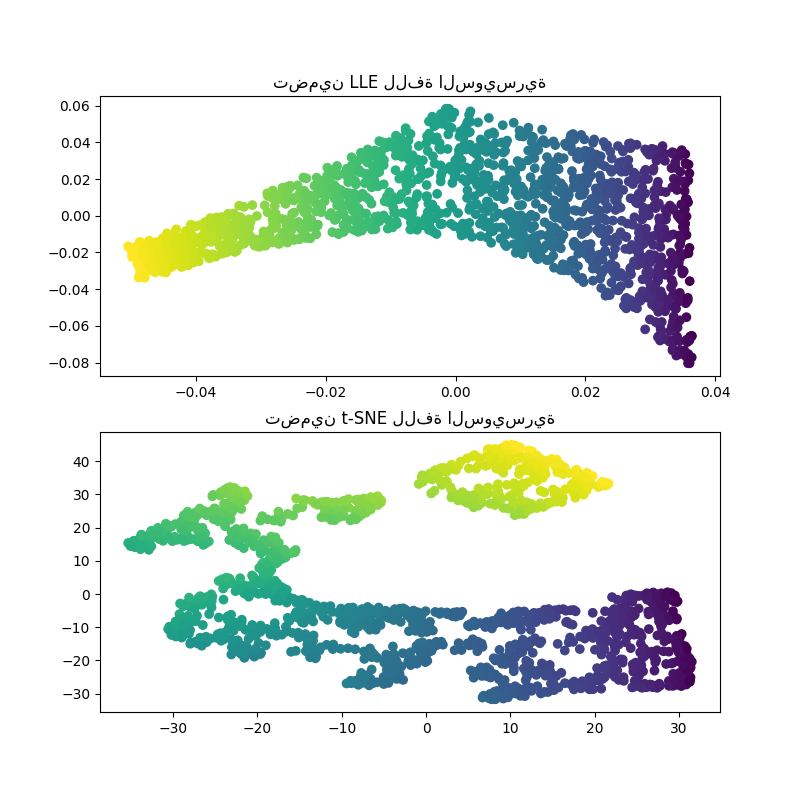
بحساب تضمينات LLE وt-SNE، نجد أن LLE يبدو أنه يفرد اللفافة السويسرية بشكل فعال جدًا. من ناحية أخرى، فإن t-SNE قادر على الحفاظ على الهيكل العام للبيانات، ولكنه يمثل بشكل سيئ الطبيعة المستمرة لبياناتنا الأصلية. بدلاً من ذلك، يبدو أنه يجمع بشكل غير ضروري أقسامًا من النقاط معًا.
sr_lle, sr_err = manifold.locally_linear_embedding(
sr_points, n_neighbors=12, n_components=2
)
sr_tsne = manifold.TSNE(n_components=2, perplexity=40, random_state=0).fit_transform(
sr_points
)
fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sr_lle[:, 0], sr_lle[:, 1], c=sr_color)
axs[0].set_title("تضمين LLE للفة السويسرية")
axs[1].scatter(sr_tsne[:, 0], sr_tsne[:, 1], c=sr_color)
_ = axs[1].set_title("تضمين t-SNE للفة السويسرية")
ملاحظة
يبدو أن LLE يمد النقاط من مركز (أرجواني) اللفة السويسرية. ومع ذلك، نلاحظ أن هذا مجرد نتيجة ثانوية لكيفية إنشاء البيانات. هناك كثافة أعلى للنقاط بالقرب من مركز اللفة، مما يؤثر في النهاية على كيفية إعادة بناء LLE للبيانات في بُعد أقل.
اللفافة السويسرية ذات الثقب#
الآن دعونا نلقي نظرة على كيفية تعامل كلتا الخوارزميتين مع إضافة ثقب إلى البيانات. أولاً، نقوم بإنشاء مجموعة بيانات اللفافة السويسرية ذات الثقب ورسمها:
sh_points, sh_color = datasets.make_swiss_roll(
n_samples=1500, hole=True, random_state=0
)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
sh_points[:, 0], sh_points[:, 1], sh_points[:, 2], c=sh_color, s=50, alpha=0.8
)
ax.set_title("اللفافة السويسرية ذات الثقب في الفضاء المحيط")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)
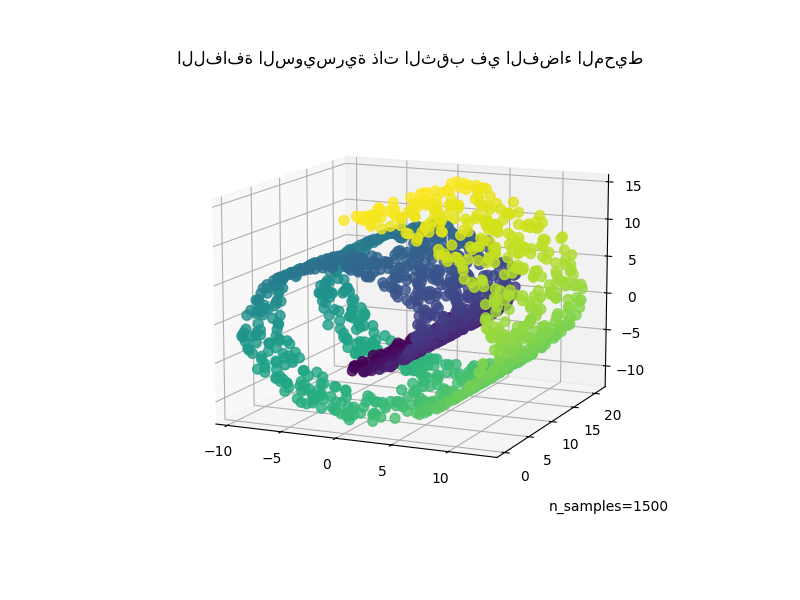
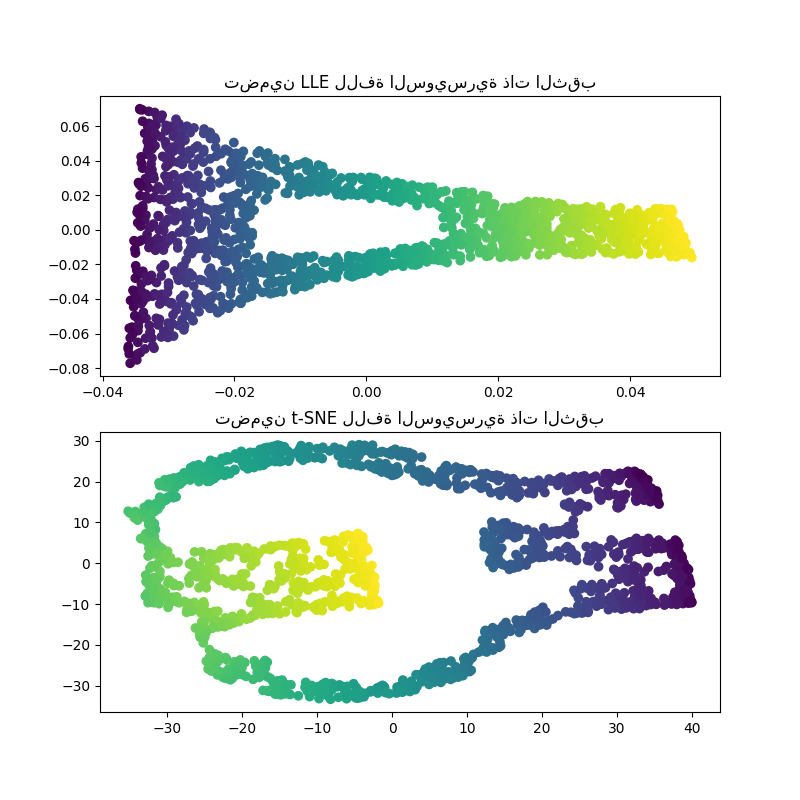
بحساب تضمينات LLE وt-SNE، نحصل على نتائج مماثلة للفة السويسرية. يقوم LLE بفك البيانات بشكل فعال للغاية ويحافظ على الثقب. يبدو أن t-SNE يجمع أقسامًا من النقاط معًا مرة أخرى، لكننا نلاحظ أنه يحافظ على الهيكل العام للبيانات الأصلية.
sh_lle, sh_err = manifold.locally_linear_embedding(
sh_points, n_neighbors=12, n_components=2
)
sh_tsne = manifold.TSNE(
n_components=2, perplexity=40, init="random", random_state=0
).fit_transform(sh_points)
fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sh_lle[:, 0], sh_lle[:, 1], c=sh_color)
axs[0].set_title("تضمين LLE للفة السويسرية ذات الثقب")
axs[1].scatter(sh_tsne[:, 0], sh_tsne[:, 1], c=sh_color)
_ = axs[1].set_title("تضمين t-SNE للفة السويسرية ذات الثقب")
ملاحظات ختامية#
نلاحظ أن t-SNE تستفيد من اختبار المزيد من مجموعات المعلمات. ربما كان من الممكن الحصول على نتائج أفضل عن طريق ضبط هذه المعلمات بشكل أفضل.
نلاحظ أنه، كما هو موضح في مثال "تعلم متعدد الشعب على أرقام مكتوبة بخط اليد"، فإن t-SNE بشكل عام يؤدي أداءً أفضل من LLE على بيانات العالم الحقيقي.
Total running time of the script: (0 minutes 12.555 seconds)
Related examples

تعلم متعدد الشعب على الأرقام المكتوبة بخط اليد: التضمين الخطي المحلي، Isomap...