المقارنة الإحصائية للنماذج باستخدام البحث الشبكي

يوضح هذا المثال كيفية المقارنة الإحصائية لأداء النماذج المدربة والمقيمة باستخدام GridSearchCV.

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

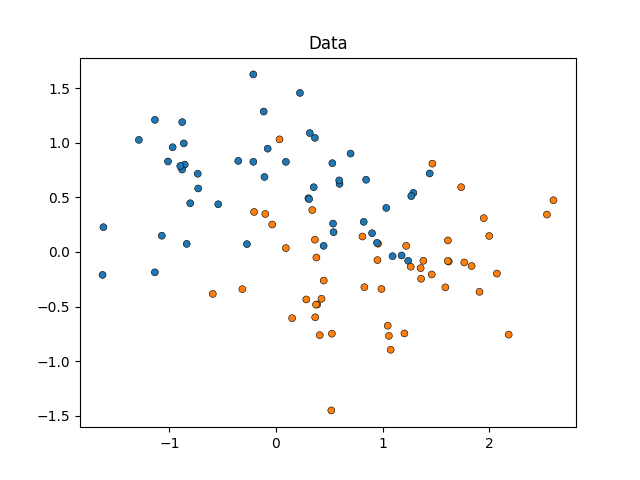
سنبدأ بمحاكاة بيانات على شكل قمر (حيث يكون الفصل المثالي بين الفئات غير خطي)، مع إضافة درجة معتدلة من الضوضاء. ستنتمي نقاط البيانات إلى واحدة من فئتين محتملتين للتنبؤ بهما باستخدام ميزتين. سنحاكي 50 عينة لكل فئة:

import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.datasets import make_moons

X, y = make_moons(noise=0.352, random_state=1, n_samples=100)

sns.scatterplot(
    x=X[:, 0], y=X[:, 1], hue=y, marker="o", s=25, edgecolor="k", legend=False
).set_title("Data")
plt.show()

سنقارن أداء SVC estimators التي تختلف في معاملها 'kernel'، لتحديد أي خيار لهذا المعامل الفرعي يتنبأ ببياناتنا المحاكاة بشكل أفضل. سنقيم أداء النماذج باستخدام RepeatedStratifiedKFold، مع تكرار 10 مرات تقسيم البيانات إلى 10 مجموعات مع تقسيم استراتيجي، مع استخدام تقسيم عشوائي مختلف للبيانات في كل تكرار. سيتم تقييم الأداء باستخدام roc_auc_score.

from sklearn.model_selection import GridSearchCV, RepeatedStratifiedKFold
from sklearn.svm import SVC

param_grid = [
    {"kernel": ["linear"]},
    {"kernel": ["poly"], "degree": [2, 3]},
    {"kernel": ["rbf"]},
]

svc = SVC(random_state=0)

cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=10, random_state=0)

search = GridSearchCV(estimator=svc, param_grid=param_grid, scoring="roc_auc", cv=cv)
search.fit(X, y)

GridSearchCV(cv=RepeatedStratifiedKFold(n_repeats=10, n_splits=10, random_state=0),
             estimator=SVC(random_state=0),
             param_grid=[{'kernel': ['linear']},
                         {'degree': [2, 3], 'kernel': ['poly']},
                         {'kernel': ['rbf']}],
             scoring='roc_auc')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

يمكننا الآن فحص نتائج بحثنا، مرتبة حسب mean_test_score:

import pandas as pd

results_df = pd.DataFrame(search.cv_results_)
results_df = results_df.sort_values(by=["rank_test_score"])
results_df = results_df.set_index(
    results_df["params"].apply(lambda x: "_".join(str(val) for val in x.values()))
).rename_axis("kernel")
results_df[["params", "rank_test_score", "mean_test_score", "std_test_score"]]

	params	rank_test_score	mean_test_score	std_test_score
kernel
rbf	{'kernel': 'rbf'}	1	0.9400	0.079297
linear	{'kernel': 'linear'}	2	0.9300	0.077846
3_poly	{'degree': 3, 'kernel': 'poly'}	3	0.9044	0.098776
2_poly	{'degree': 2, 'kernel': 'poly'}	4	0.6852	0.169106

يمكننا أن نرى أن المحلل باستخدام معامل 'rbf' حقق أفضل أداء، يليه 'linear' عن قرب. كل من المحللين اللذين استخدما معامل 'poly' حققا أداءً أسوأ، مع تحقيق المحلل الذي يستخدم دالة متعددة الحدود من الدرجة الثانية أداءً أقل بكثير من جميع النماذج الأخرى.

عادة، ينتهي التحليل هنا، ولكن نصف القصة مفقود. لا يوفر ناتج GridSearchCV معلومات حول اليقين من الاختلافات بين النماذج. لا نعرف إذا كانت هذه الاختلافات إحصائية مهمة. لتقييم ذلك، نحتاج إلى إجراء اختبار إحصائي. على وجه التحديد، لمقارنة أداء نموذجين يجب المقارنة الإحصائية لدرجات AUC الخاصة بهما. هناك 100 عينة (درجات AUC) لكل نموذج حيث قمنا بتكرار 10 مرات تقسيم البيانات إلى 10 مجموعات.

ومع ذلك، فإن درجات النماذج ليست مستقلة: يتم تقييم جميع النماذج على نفس 100 تقسيم، مما يزيد من الارتباط بين أداء النماذج. نظرًا لأن بعض تقسيمات البيانات يمكن أن تجعل التمييز بين الفئات سهلًا أو صعبًا بشكل خاص بالنسبة لجميع النماذج، فإن درجات النماذج ستتغير.

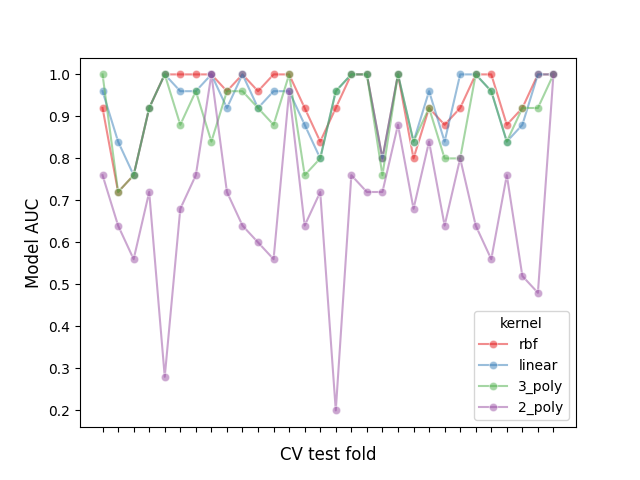
دعنا نتفقد تأثير التقسيم هذا من خلال رسم أداء جميع النماذج في كل تقسيم، وحساب الارتباط بين النماذج عبر التقسيمات:

# إنشاء إطار بيانات لدرجات النماذج مرتبة حسب الأداء
model_scores = results_df.filter(regex=r"split\d*_test_score")

# رسم 30 مثال على الاعتماد بين تقسيمات الاختبار ودرجات AUC
fig, ax = plt.subplots()
sns.lineplot(
    data=model_scores.transpose().iloc[:30],
    dashes=False,
    palette="Set1",
    marker="o",
    alpha=0.5,
    ax=ax,
)
ax.set_xlabel("CV test fold", size=12, labelpad=10)
ax.set_ylabel("Model AUC", size=12)
ax.tick_params(bottom=True, labelbottom=False)
plt.show()

# طباعة ارتباط درجات AUC عبر التقسيمات
print(f"Correlation of models:\n {model_scores.transpose().corr()}")

Correlation of models:
 kernel       rbf    linear    3_poly    2_poly
kernel
rbf     1.000000  0.882561  0.783392  0.351390
linear  0.882561  1.000000  0.746492  0.298688
3_poly  0.783392  0.746492  1.000000  0.355440
2_poly  0.351390  0.298688  0.355440  1.000000

يمكننا ملاحظة أن أداء النماذج يعتمد بشكل كبير على التقسيم.

وكنتيجة لذلك، إذا افترضنا الاستقلالية بين العينات، فسنقوم بتقليل التباين المحسوب في اختباراتنا الإحصائية، مما يزيد من عدد الأخطاء الإيجابية الخاطئة (أي اكتشاف فرق مهم بين النماذج عندما لا يوجد مثل هذا الفرق) [1]_.

تم تطوير العديد من الاختبارات الإحصائية المصححة للتباين لهذه الحالات. في هذا المثال، سنعرض كيفية تنفيذ أحد هذه الاختبارات (ما يسمى اختبار t المصحح لناديو وبنجيو) تحت إطارين إحصائيين مختلفين: الترددي والبايزي.

مقارنة نموذجين: النهج الترددي

يمكننا أن نبدأ بسؤال: "هل النموذج الأول أفضل بشكل كبير من النموذج الثاني (عند ترتيبه حسب mean_test_score)؟"

للإجابة على هذا السؤال باستخدام نهج ترددي، يمكننا إجراء اختبار t المزدوج وحساب قيمة p. وهذا ما يسمى أيضًا باختبار دييولد-ماريانو في أدبيات التنبؤ [5]_. تم تطوير العديد من المتغيرات لمثل هذا اختبار t لحساب 'مشكلة عدم استقلالية العينات' الموصوفة في القسم السابق. سنستخدم الاختبار الذي أثبت أنه يحقق أعلى درجات التكرار (التي تقيس مدى تشابه أداء نموذج عند تقييمه على تقسيمات عشوائية مختلفة لنفس مجموعة البيانات) مع الحفاظ على معدل منخفض من الأخطاء الإيجابية الخاطئة والسلبية: اختبار t المصحح لناديو وبنجيو [2]_ الذي يستخدم 10 مرات تكرار تقسيم البيانات إلى 10 مجموعات [3]_.

يتم حساب هذا الاختبار المزدوج المصحح على النحو التالي:

\[t=\frac{\frac{1}{k \cdot r}\sum_{i=1}^{k}\sum_{j=1}^{r}x_{ij}} {\sqrt{(\frac{1}{k \cdot r}+\frac{n_{test}}{n_{train}})\hat{\sigma}^2}}\]

حيث \(k\) هو عدد التقسيمات، \(r\) عدد التكرارات في التقسيم، \(x\) هو الفرق في أداء النماذج، \(n_{test}\) هو عدد العينات المستخدمة للاختبار، \(n_{train}\) هو عدد العينات المستخدمة للتدريب، و \(\hat{\sigma}^2\) يمثل تباين الاختلافات الملاحظة.

دعنا ننفذ اختبار t المزدوج المصحح لتقييم ما إذا كان أداء النموذج الأول أفضل بشكل كبير من أداء النموذج الثاني. فرضية العدم لدينا هي أن النموذج الثاني يؤدي على الأقل بنفس جودة النموذج الأول.

import numpy as np
from scipy.stats import t


def corrected_std(differences, n_train, n_test):
    """تصحيح الانحراف المعياري باستخدام نهج ناديو وبنجيو.

    المعلمات
    ----------
    differences : مصفوفة من الشكل (n_samples,)
        متجه يحتوي على الاختلافات في مقاييس درجات النموذجين.
    n_train : int
        عدد العينات في مجموعة التدريب.
    n_test : int
        عدد العينات في مجموعة الاختبار.

    العائدات
    -------
    corrected_std : float
        الانحراف المعياري المصحح للتباين لمجموعة الاختلافات.
    """
    # kr = k times r, r times repeated k-fold crossvalidation,
    # kr equals the number of times the model was evaluated
    kr = len(differences)
    corrected_var = np.var(differences, ddof=1) * (1 / kr + n_test / n_train)
    corrected_std = np.sqrt(corrected_var)
    return corrected_std


def compute_corrected_ttest(differences, df, n_train, n_test):
    """يحسب اختبار t المزدوج المصحح.

    المعلمات
    ----------
    differences : مصفوفة على شكل (n_samples,)
        متجه يحتوي على الاختلافات في مقاييس درجات النموذجين.
    df : int
        درجات الحرية.
    n_train : int
        عدد العينات في مجموعة التدريب.
    n_test : int
        عدد العينات في مجموعة الاختبار.

    العائدات
    -------
    t_stat : float
        t-statistic المصحح للتباين.
    p_val : float
        p-value المصحح للتباين.
    """
    mean = np.mean(differences)
    std = corrected_std(differences, n_train, n_test)
    t_stat = mean / std
    p_val = t.sf(np.abs(t_stat), df)  # اختبار t المزدوج المصحح
    return t_stat, p_val

model_1_scores = model_scores.iloc[0].values  # درجات النموذج الأفضل
model_2_scores = model_scores.iloc[1].values  # درجات النموذج الثاني الأفضل

differences = model_1_scores - model_2_scores

n = differences.shape[0]  # عدد مجموعات الاختبار
df = n - 1
n_train = len(list(cv.split(X, y))[0][0])
n_test = len(list(cv.split(X, y))[0][1])

t_stat, p_val = compute_corrected_ttest(differences, df, n_train, n_test)
print(f"Corrected t-value: {t_stat:.3f}\nCorrected p-value: {p_val:.3f}")

Corrected t-value: 0.750
Corrected p-value: 0.227

يمكننا مقارنة قيم t و p المصححة مع القيم غير المصححة:

t_stat_uncorrected = np.mean(differences) / np.sqrt(np.var(differences, ddof=1) / n)
p_val_uncorrected = t.sf(np.abs(t_stat_uncorrected), df)

print(
    f"Uncorrected t-value: {t_stat_uncorrected:.3f}\n"
    f"Uncorrected p-value: {p_val_uncorrected:.3f}"
)

Uncorrected t-value: 2.611
Uncorrected p-value: 0.005

باستخدام مستوى الأهمية التقليدي عند p=0.05، نلاحظ أن اختبار t غير المصحح يخلص إلى أن النموذج الأول أفضل بشكل كبير من النموذج الثاني.

مع النهج المصحح، على العكس، نفشل في اكتشاف هذا الاختلاف.

في الحالة الأخيرة، ومع ذلك، لا يسمح لنا النهج الترددي باستنتاج أن النموذج الأول والثاني لهما أداء مكافئ. إذا أردنا تأكيد ذلك، نحتاج إلى استخدام نهج بايزي.

مقارنة نموذجين: النهج البايزي

يمكننا استخدام التقدير البايزي لحساب احتمال أن النموذج الأول أفضل من النموذج الثاني. سيقوم التقدير البايزي بإخراج توزيع متبوعًا بمتوسط \(\mu\) للاختلافات في أداء النموذجين.

للحصول على التوزيع اللاحق، نحتاج إلى تحديد توزيع مسبق يمثل معتقداتنا حول كيفية توزيع المتوسط قبل النظر إلى البيانات، وضربه في دالة احتمالية تحسب مدى احتمال الاختلافات الملاحظة، مع الأخذ في الاعتبار القيم التي يمكن أن يأخذها متوسط الاختلافات.

يمكن إجراء التقدير البايزي بأشكال كثيرة للإجابة على سؤالنا، ولكن في هذا المثال سننفذ النهج المقترح من قبل بينافولي وزملائه [4]_.

إحدى طرق تحديد اللاحق باستخدام تعبير مغلق هي اختيار توزيع مسبق مؤامرة للتوزيع الاحتمالي. يظهر بينافولي وزملاؤه [4]_ أنه عند مقارنة أداء مصنفين، يمكننا نمذجة التوزيع المسبق كـ توزيع طبيعي-غاما (مع كل من المتوسط والتباين غير معروفين) مؤامرة لتوزيع احتمالي طبيعي، وبالتالي التعبير عن اللاحق كتوزيع طبيعي. عن طريق تهميش التباين من هذا اللاحق الطبيعي، يمكننا تحديد اللاحق لمعامل المتوسط كتوزيع t لطالب. على وجه التحديد:

\[St(\mu;n-1,\overline{x},(\frac{1}{n}+\frac{n_{test}}{n_{train}}) \hat{\sigma}^2)\]

حيث \(n\) هو العدد الإجمالي للعينات، \(\overline{x}\) يمثل متوسط الاختلاف في الدرجات، \(n_{test}\) هو عدد العينات المستخدمة للاختبار، \(n_{train}\) هو عدد العينات المستخدمة للتدريب، و \(\hat{\sigma}^2\) يمثل تباين الاختلافات الملاحظة.

لاحظ أننا نستخدم تباين ناديو وبنجيو المصحح في نهجنا البايزي أيضًا.

دعنا نحسب ونرسم التوزيع اللاحق:

# تهيئة المتغير العشوائي
t_post = t(
    df, loc=np.mean(differences), scale=corrected_std(differences, n_train, n_test)
)

دعنا نرسم التوزيع اللاحق:

x = np.linspace(t_post.ppf(0.001), t_post.ppf(0.999), 100)

plt.plot(x, t_post.pdf(x))
plt.xticks(np.arange(-0.04, 0.06, 0.01))
plt.fill_between(x, t_post.pdf(x), 0, facecolor="blue", alpha=0.2)
plt.ylabel("Probability density")
plt.xlabel(r"Mean difference ($\mu$)")
plt.title("Posterior distribution")
plt.show()

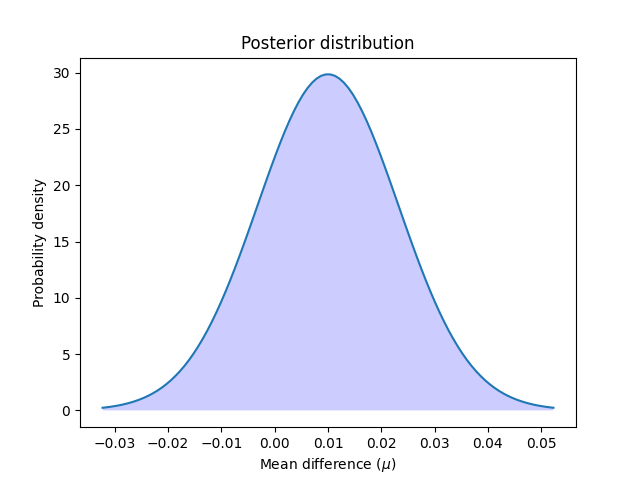
يمكننا حساب احتمال أن النموذج الأول أفضل من النموذج الثاني عن طريق حساب المساحة تحت المنحنى للتوزيع اللاحق من الصفر إلى ما لا نهاية. وبالعكس: يمكننا حساب احتمال أن النموذج الثاني أفضل من النموذج الأول عن طريق حساب المساحة تحت المنحنى من ما لا نهاية إلى الصفر.

better_prob = 1 - t_post.cdf(0)

print(
    f"Probability of {model_scores.index[0]} being more accurate than "
    f"{model_scores.index[1]}: {better_prob:.3f}"
)
print(
    f"Probability of {model_scores.index[1]} being more accurate than "
    f"{model_scores.index[0]}: {1 - better_prob:.3f}"
)

Probability of rbf being more accurate than linear: 0.773
Probability of linear being more accurate than rbf: 0.227

على عكس النهج الترددي، يمكننا حساب احتمال أن يكون أحد النموذجين أفضل من الآخر.

Related examples

"

"

استراتيجية إعادة الضبط المخصصة للبحث الشبكي مع التحقق المتقاطع

استراتيجية إعادة الضبط المخصصة للبحث الشبكي مع التحقق المتقاطع

# مقارنة المنحنيات الخطية للانحدار البايزي

# مقارنة المنحنيات الخطية للانحدار البايزي

مثال على خط أنابيب لاستخراج ميزات النص وتقييمها

مثال على خط أنابيب لاستخراج ميزات النص وتقييمها