ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
رسم مجموعة بيانات متعددة التصنيفات مُولدة عشوائياً#
هذا يوضح مولد مجموعة البيانات make_multilabel_classification
. تتكون كل عينة من عدد من ميزتين (حتى 50 في المجموع)، والتي تُوزع بشكل مختلف في كل من الفئتين.
تُصنف النقاط على النحو التالي، حيث يشير Y إلى وجود الفئة:
1 |
2 |
3 |
Color |
|---|---|---|---|
Y |
N |
N |
Red |
N |
Y |
N |
Blue |
N |
N |
Y |
Yellow |
Y |
Y |
N |
Purple |
Y |
N |
Y |
Orange |
Y |
Y |
N |
Green |
Y |
Y |
Y |
Brown |
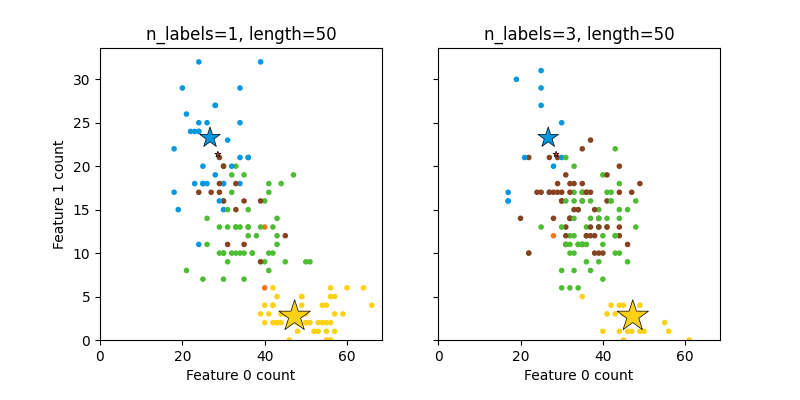
يُشير النجم إلى العينة المتوقعة لكل فئة؛ ويعكس حجمه احتمالية اختيار هذا التصنيف.
تُبرز الأمثلة على اليسار واليمين معامل "n_labels": حيث يوجد المزيد من العينات في الرسم البياني على اليمين والتي لديها 2 أو 3 تصنيفات.
ملاحظة: هذا المثال ثنائي الأبعاد مُنحرف جداً: بشكل عام، سيكون عدد الميزات أكبر بكثير من "طول الوثيقة"، في حين أن لدينا هنا وثائق أكبر بكثير من المفردات. وبالمثل، مع "n_classes > n_features"، من غير المرجح أن تُميز ميزة فئة معينة.
The data was generated from (random_state=767):
Class P(C) P(w0|C) P(w1|C)
red 0.01 0.57 0.43
blue 0.38 0.53 0.47
yellow 0.60 0.95 0.05
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_multilabel_classification as make_ml_clf
COLORS = np.array(
[
"!",
"#FF3333", # red
"#0198E1", # blue
"#BF5FFF", # purple
"#FCD116", # yellow
"#FF7216", # orange
"#4DBD33", # green
"#87421F", # brown
]
)
# استخدام نفس البذرة العشوائية لعدة مكالمات إلى make_multilabel_classification ل
# ضمان نفس التوزيعات
RANDOM_SEED = np.random.randint(2**10)
def plot_2d(ax, n_labels=1, n_classes=3, length=50):
X, Y, p_c, p_w_c = make_ml_clf(
n_samples=150,
n_features=2,
n_classes=n_classes,
n_labels=n_labels,
length=length,
allow_unlabeled=False,
return_distributions=True,
random_state=RANDOM_SEED,
)
ax.scatter(
X[:, 0], X[:, 1], color=COLORS.take((Y * [1, 2, 4]).sum(axis=1)), marker="."
)
ax.scatter(
p_w_c[0] * length,
p_w_c[1] * length,
marker="*",
linewidth=0.5,
edgecolor="black",
s=20 + 1500 * p_c**2,
color=COLORS.take([1, 2, 4]),
)
ax.set_xlabel("Feature 0 count")
return p_c, p_w_c
_, (ax1, ax2) = plt.subplots(1, 2, sharex="row", sharey="row", figsize=(8, 4))
plt.subplots_adjust(bottom=0.15)
p_c, p_w_c = plot_2d(ax1, n_labels=1)
ax1.set_title("n_labels=1, length=50")
ax1.set_ylabel("Feature 1 count")
plot_2d(ax2, n_labels=3)
ax2.set_title("n_labels=3, length=50")
ax2.set_xlim(left=0, auto=True)
ax2.set_ylim(bottom=0, auto=True)
plt.show()
print("The data was generated from (random_state=%d):" % RANDOM_SEED)
print("Class", "P(C)", "P(w0|C)", "P(w1|C)", sep="\t")
for k, p, p_w in zip(["red", "blue", "yellow"], p_c, p_w_c.T):
print("%s\t%0.2f\t%0.2f\t%0.2f" % (k, p, p_w[0], p_w[1]))
Total running time of the script: (0 minutes 0.175 seconds)
Related examples
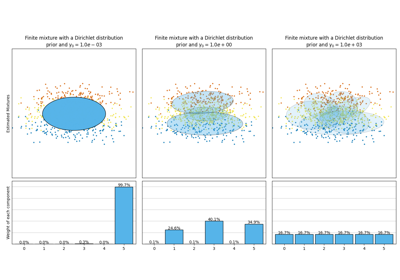
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر