ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

عرض توضيحي لخوارزمية التجميع متوسط التحول#

المرجع:

دورين كومانيسيو وبيتر مير، "متوسط التحول: نهج قوي نحو تحليل مساحة الميزات". معاملات IEEE على تحليل الأنماط والذكاء الاصطناعي. 2002. ص 603-619.

# المؤلفون: مطوري سكايت-ليرن
# معرف الترخيص-SPDX: BSD-3-Clause

import numpy as np

from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs

توليد بيانات العينة#

centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)

حساب التجميع باستخدام MeanShift#

# يمكن الكشف عن عرض النطاق الترددي التالي تلقائيًا باستخدام
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)

ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)

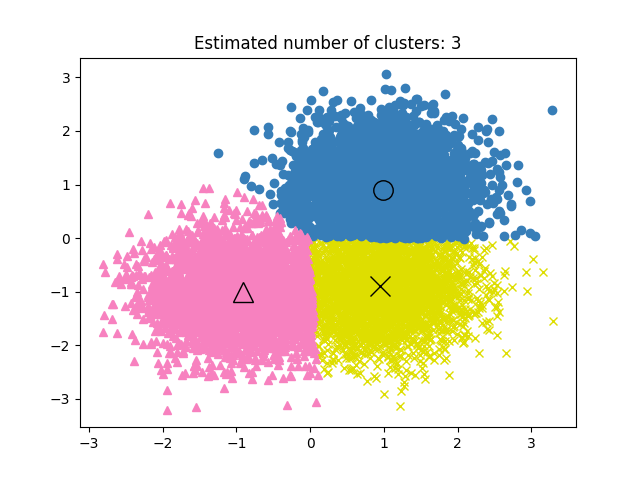
print("عدد التجمعات المقدرة: %d" % n_clusters_)

عدد التجمعات المقدرة: 3

رسم النتيجة#

import matplotlib.pyplot as plt

plt.figure(1)
plt.clf()

colors = ["#dede00", "#377eb8", "#f781bf"]
markers = ["x", "o", "^"]

for k, col in zip(range(n_clusters_), colors):
    my_members = labels == k
    cluster_center = cluster_centers[k]
    plt.plot(X[my_members, 0], X[my_members, 1], markers[k], color=col)
    plt.plot(
        cluster_center[0],
        cluster_center[1],
        markers[k],
        markerfacecolor=col,
        markeredgecolor="k",
        markersize=14,
    )
plt.title("Estimated number of clusters: %d" % n_clusters_)
plt.show()