ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

الميزات في أشجار التعزيز المتدرج للهيستوغرام#

قد تكون نماذج تعزيز التدرج القائم على الرسم البياني (HGBT) واحدة من أكثر نماذج التعلم الخاضع للإشراف فائدة في scikit-learn. إنها تستند إلى تطبيق حديث للتعزيز المتدرج قابل للمقارنة مع LightGBM و XGBoost. على هذا النحو، تتميز نماذج HGBT بميزات أكثر ثراءً وغالبًا ما تتفوق في الأداء على النماذج البديلة مثل الغابات العشوائية، خاصةً عندما يكون عدد العينات أكبر من عشرات الآلاف (انظر مقارنة بين نماذج الغابات العشوائية ورفع التدرج بالرسم البياني).

أهم ميزات قابلية الاستخدام لنماذج HGBT هي:

  1. العديد من دوال الخسارة المتاحة لمهام انحدار المتوسط ​​والكمي، انظر خسارة الكم.

  2. دعم الميزات الفئوية، انظر دعم الميزات التصنيفية في التدرج التعزيزي.

  3. التوقف المبكر.

  4. دعم القيم المفقودة، مما يتجنب الحاجة إلى أداة إكمال.

  5. قيود رتيبة.

  6. قيود التفاعل.

يهدف هذا المثال إلى عرض جميع النقاط باستثناء 2 و 6 في بيئة واقعية.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

تحضير البيانات#

تتكون مجموعة بيانات الكهرباء من البيانات التي تم جمعها من سوق الكهرباء في نيو ساوث ويلز بأستراليا. في هذا السوق، الأسعار غير ثابتة وتتأثر بالعرض والطلب. يتم تحديدها كل خمس دقائق. تم إجراء عمليات نقل الكهرباء من / إلى ولاية فيكتوريا المجاورة للتخفيف من التقلبات.

تحتوي مجموعة البيانات، المسماة في الأصل ELEC2، على 45312 مثيلًا مؤرخة من 7 مايو 1996 إلى 5 ديسمبر 1998. يشير كل نموذج من مجموعة البيانات إلى فترة 30 دقيقة، أي هناك 48 مثيلًا لكل فترة زمنية ليوم واحد. يحتوي كل نموذج في مجموعة البيانات على 7 أعمدة:

  • التاريخ: بين 7 مايو 1996 إلى 5 ديسمبر 1998. تم تطبيعها بين 0 و 1؛

  • اليوم: يوم الأسبوع (1-7)؛

  • الفترة: فترات نصف ساعة على مدار 24 ساعة. تم تطبيعها بين 0 و 1؛

  • nswprice / nswdemand: سعر / طلب الكهرباء في نيو ساوث ويلز؛

  • vicprice / vicdemand: سعر / طلب الكهرباء في فيكتوريا.

في الأصل، إنها مهمة تصنيف، لكننا نستخدمها هنا لمهمة الانحدار للتنبؤ بنقل الكهرباء المجدول بين الولايات.

from sklearn.datasets import fetch_openml

electricity = fetch_openml(
    name="electricity", version=1, as_frame=True, parser="pandas"
)
df = electricity.frame

تحتوي مجموعة البيانات هذه على هدف ثابت تدريجي لأول 17760 نموذجًا:

df["transfer"][:17_760].unique()

array([0.414912, 0.500526])

دعونا نتخلص من هذه الإدخالات ونستكشف نقل الكهرباء كل ساعة على مدار أيام مختلفة من الأسبوع:

import matplotlib.pyplot as plt
import seaborn as sns

df = electricity.frame.iloc[17_760:]
X = df.drop(columns=["transfer", "class"])
y = df["transfer"]

fig, ax = plt.subplots(figsize=(15, 10))
pointplot = sns.lineplot(x=df["period"], y=df["transfer"], hue=df["day"], ax=ax)
handles, lables = ax.get_legend_handles_labels()
ax.set(
    title="نقل الطاقة كل ساعة لأيام مختلفة من الأسبوع",
    xlabel="الوقت الطبيعي من اليوم",
    ylabel="نقل الطاقة الطبيعي",
)
_ = ax.legend(handles, ["الأحد", "الاثنين", "الثلاثاء", "الأربعاء", "الخميس", "الجمعة", "السبت"])
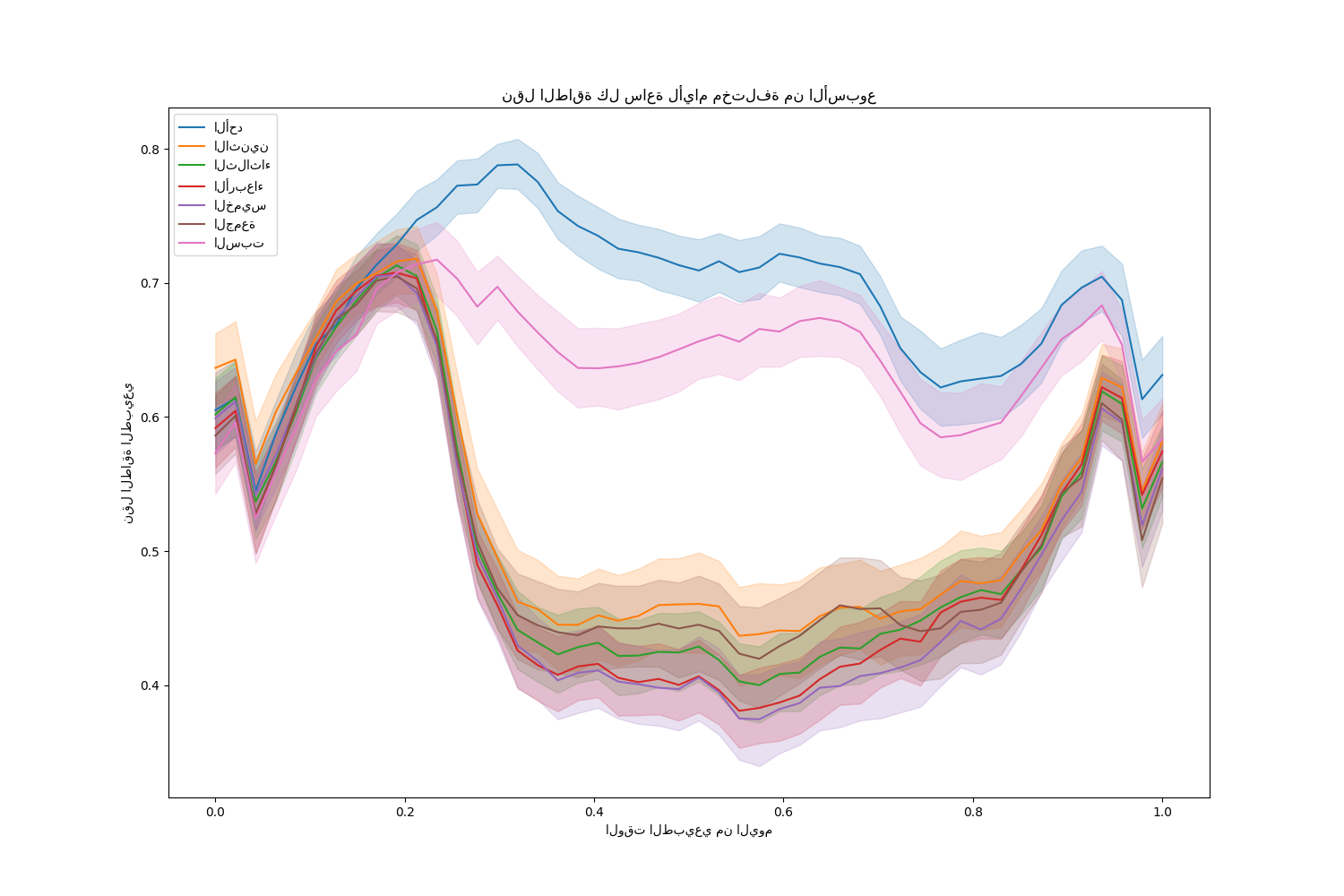
نقل الطاقة كل ساعة لأيام مختلفة من الأسبوع

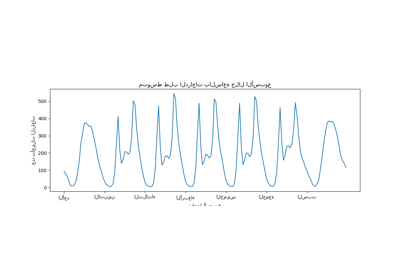
لاحظ أن نقل الطاقة يزداد بشكل منهجي خلال عطلات نهاية الأسبوع.

تأثير عدد الأشجار والتوقف المبكر#

من أجل توضيح تأثير (الحد الأقصى) لعدد الأشجار، نقوم بتدريب HistGradientBoostingRegressor على نقل الكهرباء اليومي باستخدام مجموعة البيانات بأكملها. ثم نقوم بتصور تنبؤاتها اعتمادًا على معلمة max_iter. هنا لا نحاول تقييم أداء النموذج وقدرته على التعميم ولكن بالأحرى قدرته على التعلم من بيانات التدريب.

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle=False)

print(f"حجم عينة التدريب: {X_train.shape[0]}")
print(f"حجم عينة الاختبار: {X_test.shape[0]}")
print(f"عدد الميزات: {X_train.shape[1]}")

حجم عينة التدريب: 16531
حجم عينة الاختبار: 11021
عدد الميزات: 7

max_iter_list = [5, 50]
average_week_demand = (
    df.loc[X_test.index].groupby(["day", "period"], observed=False)["transfer"].mean()
)
colors = sns.color_palette("colorblind")
fig, ax = plt.subplots(figsize=(10, 5))
average_week_demand.plot(color=colors[0], label="المتوسط المسجل", linewidth=2, ax=ax)

for idx, max_iter in enumerate(max_iter_list):
    hgbt = HistGradientBoostingRegressor(
        max_iter=max_iter, categorical_features=None, random_state=42
    )
    hgbt.fit(X_train, y_train)

    y_pred = hgbt.predict(X_test)
    prediction_df = df.loc[X_test.index].copy()
    prediction_df["y_pred"] = y_pred
    average_pred = prediction_df.groupby(["day", "period"], observed=False)[
        "y_pred"
    ].mean()
    average_pred.plot(
        color=colors[idx + 1], label=f"max_iter={max_iter}", linewidth=2, ax=ax
    )

ax.set(
    title="متوسط ​​نقل الطاقة المتوقع خلال الأسبوع",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["الأحد", "الاثنين", "الثلاثاء", "الأربعاء", "الخميس", "الجمعة", "السبت"],
    xlabel="وقت الأسبوع",
    ylabel="نقل الطاقة الطبيعي",
)
_ = ax.legend()
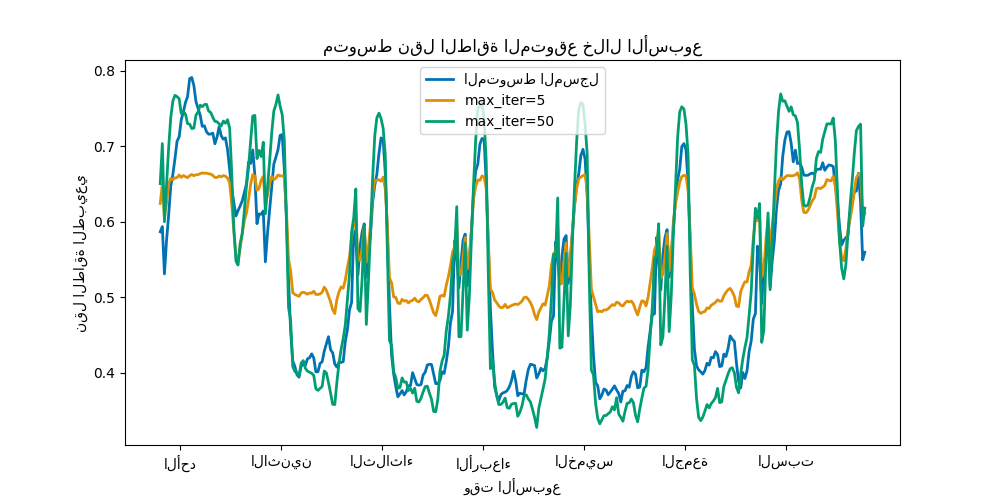
متوسط ​​نقل الطاقة المتوقع خلال الأسبوع

مع بضع تكرارات فقط، يمكن أن تحقق نماذج HGBT التقارب (انظر مقارنة بين نماذج الغابات العشوائية ورفع التدرج بالرسم البياني)، مما يعني أن إضافة المزيد من الأشجار لا يحسن النموذج بعد الآن. في الشكل أعلاه، 5 تكرارات ليست كافية للحصول على تنبؤات جيدة. مع 50 تكرارًا، نحن قادرون بالفعل على القيام بعمل جيد.

قد يؤدي تعيين max_iter مرتفعًا جدًا إلى تقليل جودة التنبؤ ويكلف الكثير من موارد الحوسبة التي يمكن تجنبها. لذلك، يوفر تطبيق HGBT في scikit-learn إستراتيجية توقف مبكر تلقائية. مع ذلك، يستخدم النموذج جزءًا من بيانات التدريب كمجموعة تحقق داخلية (validation_fraction) ويتوقف عن التدريب إذا لم تتحسن نتيجة التحقق (أو تدهورت) بعد n_iter_no_change تكرارًا حتى حد معين من التسامح (tol).

لاحظ أن هناك مفاضلة بين learning_rate و max_iter: بشكل عام، تكون معدلات التعلم الأصغر مفضلة ولكنها تتطلب المزيد من التكرارات للتقارب إلى الحد الأدنى من الخسارة، بينما تتقارب معدلات التعلم الأكبر بشكل أسرع (يتطلب تكرارات / أشجار أقل) ولكن على حساب خسارة دنيا أكبر.

نظرًا لهذا الارتباط العالي بين معدل التعلم وعدد التكرارات، فإن الممارسة الجيدة هي ضبط معدل التعلم جنبًا إلى جنب مع جميع المعلمات الفائقة (المهمة) الأخرى، ملاءمة HBGT على مجموعة التدريب بقيمة كبيرة بما يكفي لـ max_iter وتحديد أفضل max_iter عبر التوقف المبكر وبعض validation_fraction الصريحة.

common_params = {
    "max_iter": 1_000,
    "learning_rate": 0.3,
    "validation_fraction": 0.2,
    "random_state": 42,
    "categorical_features": None,
    "scoring": "neg_root_mean_squared_error",
}

hgbt = HistGradientBoostingRegressor(early_stopping=True, **common_params)
hgbt.fit(X_train, y_train)

_, ax = plt.subplots()
plt.plot(-hgbt.validation_score_)
_ = ax.set(
    xlabel="عدد التكرارات",
    ylabel="جذر متوسط ​​مربع الخطأ",
    title=f"خسارة hgbt مع التوقف المبكر (n_iter={hgbt.n_iter_})",
)
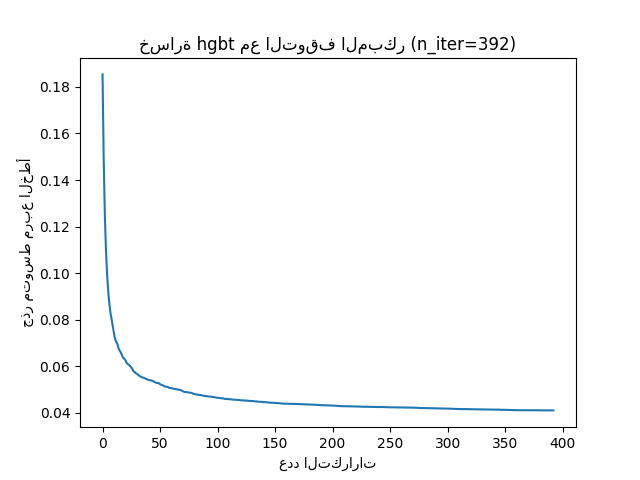
خسارة hgbt مع التوقف المبكر (n_iter=392)

يمكننا بعد ذلك الكتابة فوق قيمة max_iter إلى قيمة معقولة وتجنب التكلفة الحسابية الإضافية للتحقق الداخلي. قد يفسر تقريب عدد التكرارات تقلب مجموعة التدريب:

import math

common_params["max_iter"] = math.ceil(hgbt.n_iter_ / 100) * 100
common_params["early_stopping"] = False
hgbt = HistGradientBoostingRegressor(**common_params)

ملاحظة

التحقق الداخلي الذي يتم إجراؤه أثناء التوقف المبكر ليس هو الأمثل لسلسلة زمنية.

دعم القيم المفقودة#

تدعم نماذج HGBT القيم المفقودة بشكل أصلي. أثناء التدريب، يقرر مزارع الشجرة أين يجب أن تذهب العينات ذات القيم المفقودة (الطفل الأيسر أو الطفل الأيمن) عند كل تقسيم، بناءً على المكسب المحتمل. عند التنبؤ، يتم إرسال هذه العينات إلى الطفل المتعلم وفقًا لذلك. إذا لم يكن لدى ميزة قيم مفقودة أثناء التدريب، فعند التنبؤ، يتم إرسال العينات ذات القيم المفقودة لتلك الميزة إلى الطفل الذي يحتوي على معظم العينات (كما هو موضح أثناء الملاءمة).

يوضح هذا المثال كيفية تعامل انحدارات HGBT مع القيم المفقودة تمامًا بشكل عشوائي (MCAR)، أي أن الفقد لا يعتمد على البيانات المرصودة أو البيانات غير المرصودة. يمكننا محاكاة مثل هذا السيناريو عن طريق استبدال القيم بشكل عشوائي من ميزات مختارة عشوائيًا بقيم nan.

import numpy as np

from sklearn.metrics import root_mean_squared_error

rng = np.random.RandomState(42)
first_week = slice(0, 336)  # الأسبوع الأول في مجموعة الاختبار هو 7 * 48 = 336
missing_fraction_list = [0, 0.01, 0.03]


def generate_missing_values(X, missing_fraction):
    total_cells = X.shape[0] * X.shape[1]
    num_missing_cells = int(total_cells * missing_fraction)
    row_indices = rng.choice(X.shape[0], num_missing_cells, replace=True)
    col_indices = rng.choice(X.shape[1], num_missing_cells, replace=True)
    X_missing = X.copy()
    X_missing.iloc[row_indices, col_indices] = np.nan
    return X_missing


fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="النقل الفعلي")

for missing_fraction in missing_fraction_list:
    X_train_missing = generate_missing_values(X_train, missing_fraction)
    X_test_missing = generate_missing_values(X_test, missing_fraction)
    hgbt.fit(X_train_missing, y_train)
    y_pred = hgbt.predict(X_test_missing[first_week])
    rmse = root_mean_squared_error(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"missing_fraction={missing_fraction}, RMSE={rmse:.3f}",
        alpha=0.5,
    )
ax.set(
    title="التنبؤات اليومية بنقل الطاقة على البيانات ذات قيم MCAR",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["الاثنين", "الثلاثاء", "الأربعاء", "الخميس", "الجمعة", "السبت", "الأحد"],
    xlabel="وقت الأسبوع",
    ylabel="نقل الطاقة الطبيعي",
)
_ = ax.legend(loc="lower right")
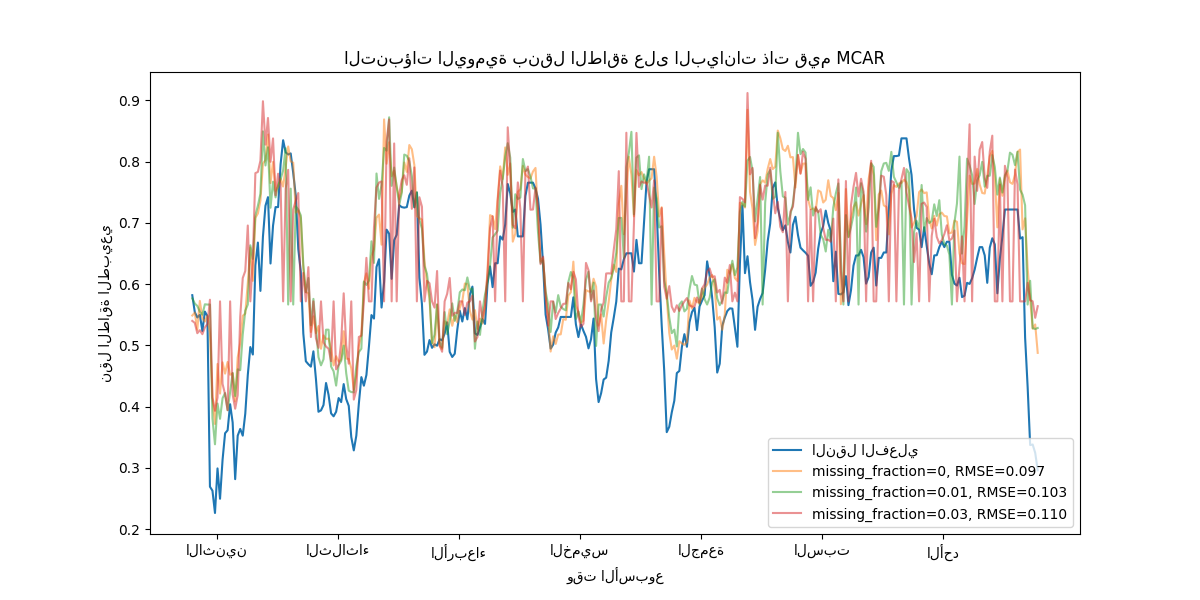
التنبؤات اليومية بنقل الطاقة على البيانات ذات قيم MCAR

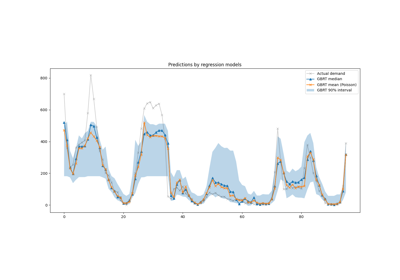
كما هو متوقع، يتدهور النموذج مع زيادة نسبة القيم المفقودة.

دعم خسارة الكم#

خسارة الكم في الانحدار تمكن من رؤية تباين أو عدم يقين المتغير الهدف. على سبيل المثال، يمكن أن يوفر التنبؤ بالحد الأدنى الخامس والحد الأقصى 95 فاصل تنبؤ بنسبة 90%، أي النطاق الذي نتوقع أن تقع فيه قيمة جديدة ملحوظة باحتمال 90%.

from sklearn.metrics import mean_pinball_loss

quantiles = [0.95, 0.05]
predictions = []

fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="النقل الفعلي")

for quantile in quantiles:
    hgbt_quantile = HistGradientBoostingRegressor(
        loss="quantile", quantile=quantile, **common_params
    )
    hgbt_quantile.fit(X_train, y_train)
    y_pred = hgbt_quantile.predict(X_test[first_week])

    predictions.append(y_pred)
    score = mean_pinball_loss(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"quantile={quantile}, pinball loss={score:.2f}",
        alpha=0.5,
    )

ax.fill_between(
    range(len(predictions[0][first_week])),
    predictions[0][first_week],
    predictions[1][first_week],
    color=colors[0],
    alpha=0.1,
)
ax.set(
    title="التنبؤات اليومية بنقل الطاقة مع خسارة الكم",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["الاثنين", "الثلاثاء", "الأربعاء", "الخميس", "الجمعة", "السبت", "الأحد"],
    xlabel="وقت الأسبوع",
    ylabel="نقل الطاقة الطبيعي",
)
_ = ax.legend(loc="lower right")
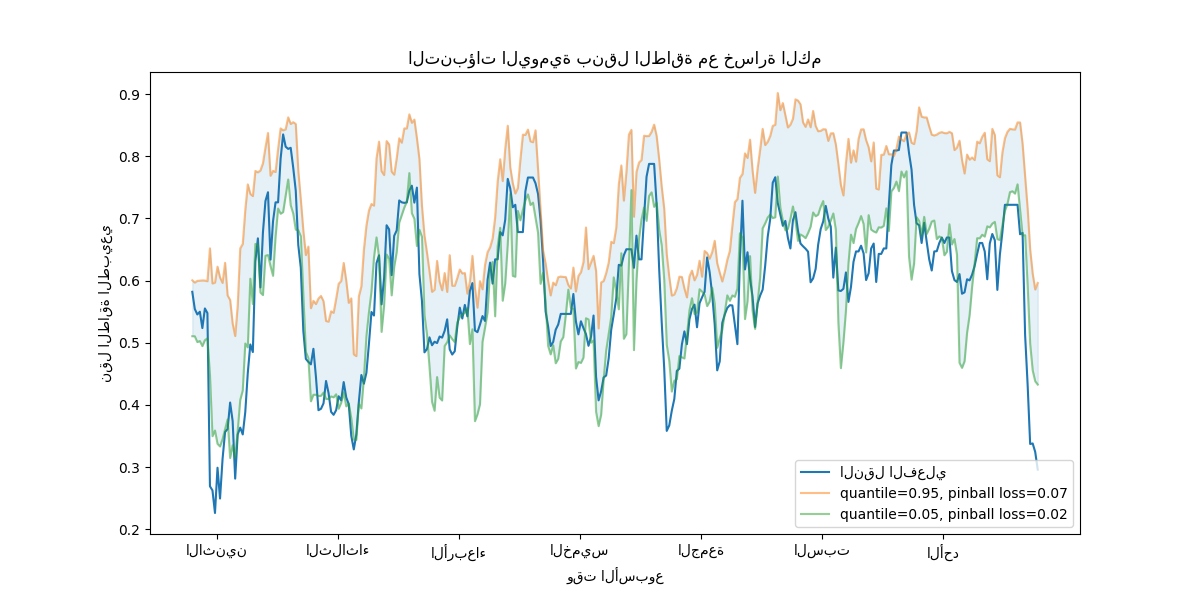
التنبؤات اليومية بنقل الطاقة مع خسارة الكم

نلاحظ ميلًا إلى المبالغة في تقدير نقل الطاقة. يمكن تأكيد ذلك كميًا عن طريق حساب أرقام التغطية التجريبية كما هو موضح في قسم معايرة فترات الثقة. ضع في اعتبارك أن هذه النسب المئوية المتوقعة هي مجرد تقديرات من نموذج. لا يزال بإمكان المرء تحسين جودة هذه التقديرات عن طريق:

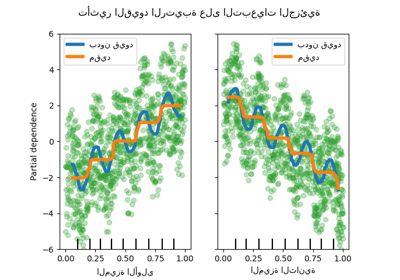
قيود رتيبة#

بالنظر إلى معرفة مجال محددة تتطلب أن تكون العلاقة بين ميزة والهدف رتيبة متزايدة أو متناقصة، يمكن للمرء فرض مثل هذا السلوك في تنبؤات نموذج HGBT باستخدام قيود رتيبة. وهذا يجعل النموذج أكثر قابلية للتفسير ويمكن أن يقلل من تباينه (ويحتمل أن يخفف من فرط التخصيص) مع خطر زيادة التحيز. يمكن أيضًا استخدام القيود الرتيبة لفرض متطلبات تنظيمية محددة، وضمان الامتثال ومحاذاة الاعتبارات الأخلاقية.

في هذا المثال، تهدف سياسة نقل الطاقة من فيكتوريا إلى نيو ساوث ويلز إلى تخفيف تقلبات الأسعار، مما يعني أن تنبؤات النموذج يجب أن تفرض مثل هذا الهدف، أي يجب أن يزداد النقل مع السعر والطلب في نيو ساوث ويلز، ولكن أيضًا يتناقص مع السعر والطلب في فيكتوريا، من أجل إفادة كلا السكانين.

إذا كانت بيانات التدريب تحتوي على أسماء ميزات، فمن الممكن تحديد القيود الرتيبة عن طريق تمرير قاموس بالاصطلاح التالي:

  • 1: زيادة رتيبة

  • 0: بدون قيود

  • -1: نقصان رتيب

بدلاً من ذلك، يمكن للمرء تمرير كائن يشبه المصفوفة يشفر الاصطلاح أعلاه حسب الموضع.

from sklearn.inspection import PartialDependenceDisplay

monotonic_cst = {
    "date": 0,
    "day": 0,
    "period": 0,
    "nswdemand": 1,
    "nswprice": 1,
    "vicdemand": -1,
    "vicprice": -1,
}
hgbt_no_cst = HistGradientBoostingRegressor(
    categorical_features=None, random_state=42
).fit(X, y)
hgbt_cst = HistGradientBoostingRegressor(
    monotonic_cst=monotonic_cst, categorical_features=None, random_state=42
).fit(X, y)

fig, ax = plt.subplots(nrows=2, figsize=(15, 10))
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "غير مقيد", "color": "tab:blue"},
    ax=ax[0],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "مقيد", "color": "tab:orange"},
    ax=disp.axes_,
)
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "غير مقيد", "color": "tab:blue"},
    ax=ax[1],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "مقيد", "color": "tab:orange"},
    ax=disp.axes_,
)
_ = plt.legend()
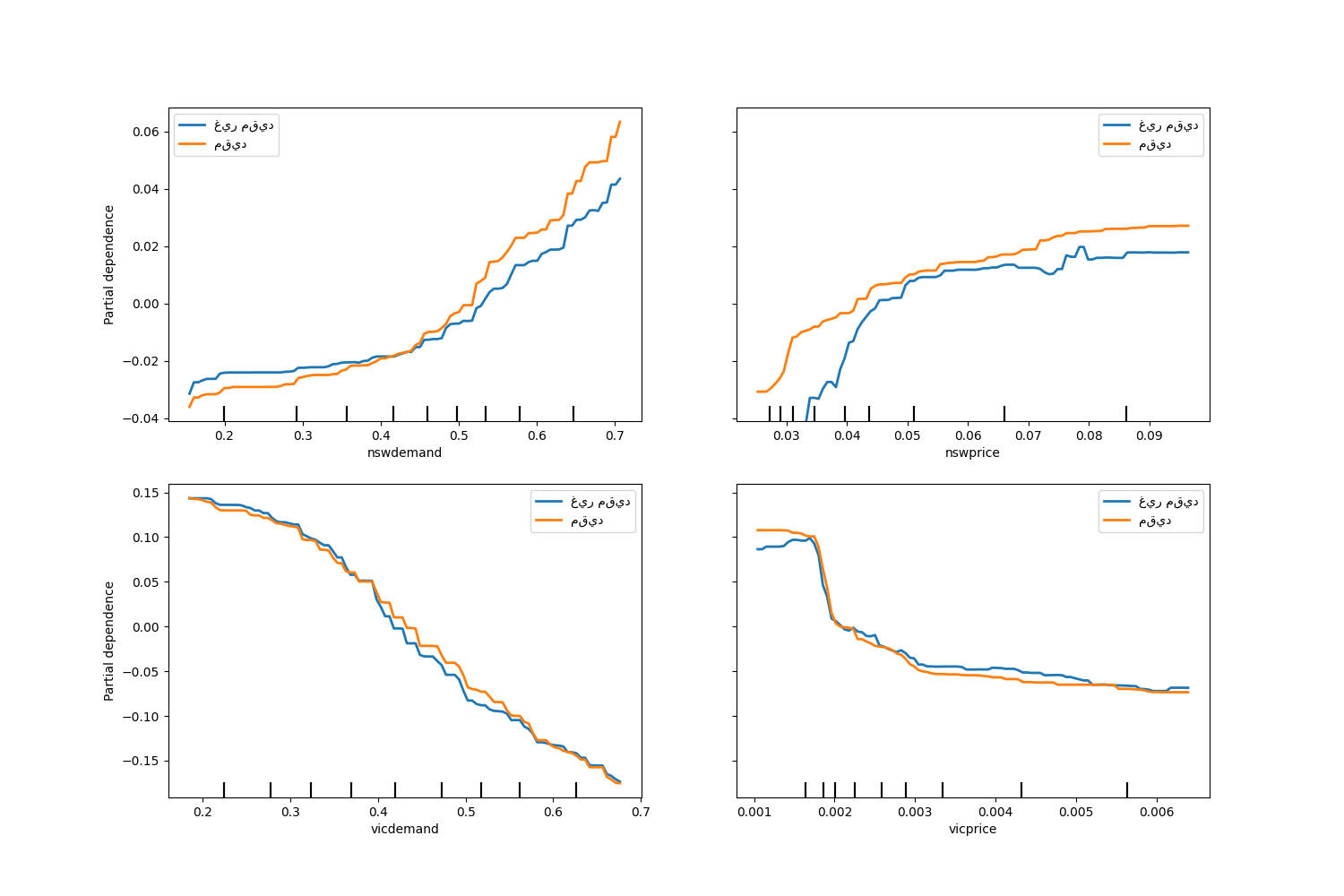
plot hgbt regression

لاحظ أن nswdemand و vicdemand يبدوان بالفعل رتيبين بدون قيود. هذا مثال جيد لإظهار أن النموذج ذو القيود الرتيبة "مقيد بشكل مفرط".

بالإضافة إلى ذلك، يمكننا التحقق من أن الجودة التنبؤية للنموذج لا تتدهور بشكل كبير عن طريق إدخال القيود الرتيبة. لهذا الغرض نستخدم TimeSeriesSplit التحقق المتقاطع لتقدير تباين نتيجة الاختبار. من خلال القيام بذلك، نضمن أن بيانات التدريب لا تتجاوز بيانات الاختبار، وهو أمر بالغ الأهمية عند التعامل مع البيانات التي لها علاقة زمنية.

from sklearn.metrics import make_scorer, root_mean_squared_error
from sklearn.model_selection import TimeSeriesSplit, cross_validate

ts_cv = TimeSeriesSplit(n_splits=5, gap=48, test_size=336)  # أسبوع يحتوي على 336 عينة
scorer = make_scorer(root_mean_squared_error)

cv_results = cross_validate(hgbt_no_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE بدون قيود = {rmse.mean():.3f} +/- {rmse.std():.3f}")

cv_results = cross_validate(hgbt_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE مع قيود    = {rmse.mean():.3f} +/- {rmse.std():.3f}")

RMSE بدون قيود = 0.103 +/- 0.030
RMSE مع قيود    = 0.107 +/- 0.034

ومع ذلك، لاحظ أن المقارنة تتم بين نموذجين مختلفين قد يتم تحسينهما بواسطة مجموعة مختلفة من المعلمات الفائقة. هذا هو السبب في أننا لا نستخدم common_params في هذا القسم كما فعلنا من قبل.

Total running time of the script: (0 minutes 28.338 seconds)

Related examples

مقارنة بين نماذج الغابات العشوائية ورفع التدرج بالرسم البياني

مقارنة بين نماذج الغابات العشوائية ورفع التدرج بالرسم البياني

القيود الرتيبة

القيود الرتيبة

هندسة الميزات ذات الصلة بالوقت

هندسة الميزات ذات الصلة بالوقت

الميزات المتأخرة للتنبؤ بالسلاسل الزمنية

الميزات المتأخرة للتنبؤ بالسلاسل الزمنية

Gallery generated by Sphinx-Gallery