ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

توضيح تحليل مكونات الأحياء المجاورة#

يوضح هذا المثال مقياس مسافة مُتعلم يُعظم دقة تصنيف أقرب الجيران. ويقدم تمثيلًا مرئيًا لهذا المقياس مقارنةً بالمساحة الأصلية للنقاط. يرجى الرجوع إلى دليل المستخدم لمزيد من المعلومات.

# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from scipy.special import logsumexp

from sklearn.datasets import make_classification
from sklearn.neighbors import NeighborhoodComponentsAnalysis

# النقاط الأصلية
# ---------------
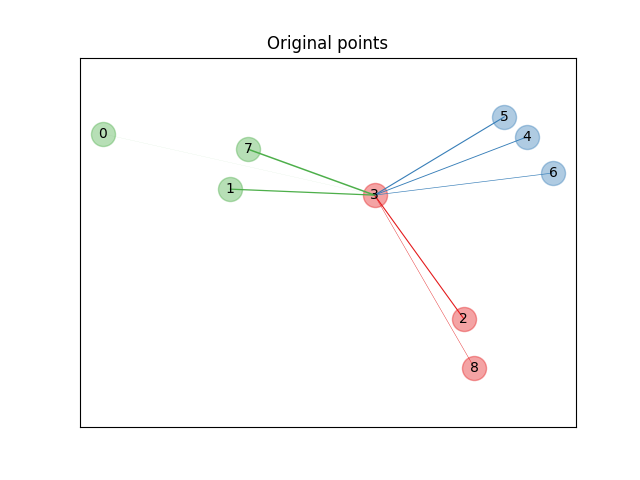
# أولًا، نقوم بإنشاء مجموعة بيانات من 9 عينات من 3 فئات، ونرسم النقاط
# في المساحة الأصلية. بالنسبة لهذا المثال، نركز على تصنيف
# النقطة رقم 3. يتناسب سمك الرابط بين النقطة رقم 3 ونقطة أخرى
# مع المسافة بينهما.

X, y = make_classification(
    n_samples=9,
    n_features=2,
    n_informative=2,
    n_redundant=0,
    n_classes=3,
    n_clusters_per_class=1,
    class_sep=1.0,
    random_state=0,
)

plt.figure(1)
ax = plt.gca()
for i in range(X.shape[0]):
    ax.text(X[i, 0], X[i, 1], str(i), va="center", ha="center")
    ax.scatter(X[i, 0], X[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)

ax.set_title("Original points")
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
ax.axis("equal")  # لعرض الحدود بشكل صحيح كدوائر

# تعريف دالة سمك الرابط
def link_thickness_i(X, i):
    diff_embedded = X[i] - X
    dist_embedded = np.einsum("ij,ij->i", diff_embedded, diff_embedded)
    dist_embedded[i] = np.inf

    # حساب المسافات الأسية (استخدام خدعة log-sum-exp لتجنب عدم الاستقرار العددي)
    exp_dist_embedded = np.exp(-dist_embedded - logsumexp(-dist_embedded))
    return exp_dist_embedded

# تعريف دالة ربط النقاط
def relate_point(X, i, ax):
    pt_i = X[i]
    for j, pt_j in enumerate(X):
        thickness = link_thickness_i(X, i)
        if i != j:
            line = ([pt_i[0], pt_j[0]], [pt_i[1], pt_j[1]])
            ax.plot(*line, c=cm.Set1(y[j]), linewidth=5 * thickness[j])

# تحديد النقطة المراد ربطها
i = 3
# ربط النقطة المحددة
relate_point(X, i, ax)
plt.show()

# تعلم التضمين
# ---------------------
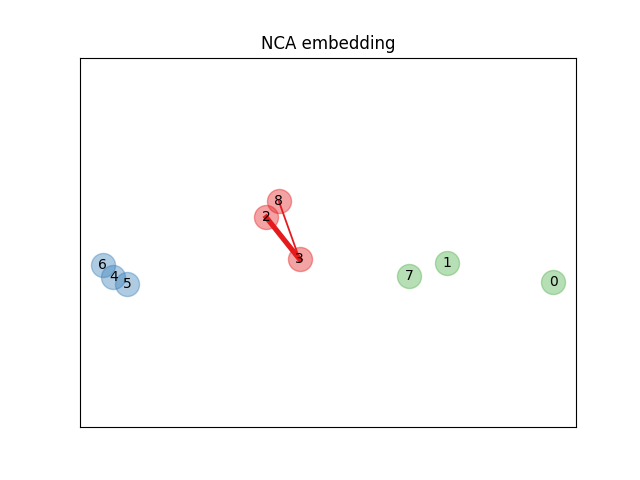
# نستخدم NeighborhoodComponentsAnalysis لتعلم التضمين
# ورسم النقاط بعد التحويل. ثم نأخذ التضمين ونحدد الجيران الأقرب.

nca = NeighborhoodComponentsAnalysis(max_iter=30, random_state=0)
nca = nca.fit(X, y)

plt.figure(2)
ax2 = plt.gca()
X_embedded = nca.transform(X)
relate_point(X_embedded, i, ax2)

for i in range(len(X)):
    ax2.text(X_embedded[i, 0], X_embedded[i, 1], str(i), va="center", ha="center")
    ax2.scatter(X_embedded[i, 0], X_embedded[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)

ax2.set_title("NCA embedding")
ax2.axes.get_xaxis().set_visible(False)
ax2.axes.get_yaxis().set_visible(False)
ax2.axis("equal")
plt.show()