ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
"#
اختبار مع التبديلات أهمية درجة التصنيف#
هذا المثال يوضح استخدام
permutation_test_score لتقييم
أهمية درجة التصنيف المتقاطعة باستخدام التبديلات.
# المؤلفون: مطوري سكايلرن
# معرف الترخيص: BSD-3-Clause
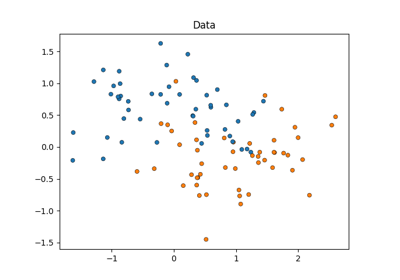
مجموعة البيانات#
سنستخدم Iris plants dataset، والتي تتكون من قياسات مأخوذة من 3 أنواع من زهرة السوسن.
سنقوم أيضًا بتوليد بعض بيانات الميزات العشوائية (أي 20 ميزة)، غير مرتبطة بعلامات الفئات في مجموعة بيانات السوسن.
import numpy as np
n_uncorrelated_features = 20
rng = np.random.RandomState(seed=0)
# استخدم نفس عدد العينات كما في iris و20 ميزة
X_rand = rng.normal(size=(X.shape[0], n_uncorrelated_features))
درجة اختبار التبديل#
بعد ذلك، نقوم بحساب
permutation_test_score باستخدام مجموعة بيانات السوسن الأصلية، والتي تتنبأ بالعلامات بقوة
والميزات العشوائية وعلامات السوسن، والتي يجب أن لا يكون لها
أي اعتماد بين الميزات والعلامات. نستخدم
SVC المصنف و:ref:accuracy_score لتقييم
النموذج في كل جولة.
permutation_test_score يولد توزيع صفري
من خلال حساب دقة المصنف
على 1000 تبديلات مختلفة لمجموعة البيانات، حيث تظل الميزات
كما هي ولكن تخضع العلامات لتبديلات مختلفة. هذا هو
التوزيع لفرضية العدم التي تنص على عدم وجود اعتماد
بين الميزات والعلامات. يتم حساب قيمة p التجريبية بعد ذلك كنسبة مئوية
من التبديلات التي تكون فيها الدرجة المحصلة أكبر
من الدرجة المحصلة باستخدام البيانات الأصلية.
from sklearn.model_selection import StratifiedKFold, permutation_test_score
from sklearn.svm import SVC
clf = SVC(kernel="linear", random_state=7)
cv = StratifiedKFold(2, shuffle=True, random_state=0)
score_iris, perm_scores_iris, pvalue_iris = permutation_test_score(
clf, X, y, scoring="accuracy", cv=cv, n_permutations=1000
)
score_rand, perm_scores_rand, pvalue_rand = permutation_test_score(
clf, X_rand, y, scoring="accuracy", cv=cv, n_permutations=1000
)
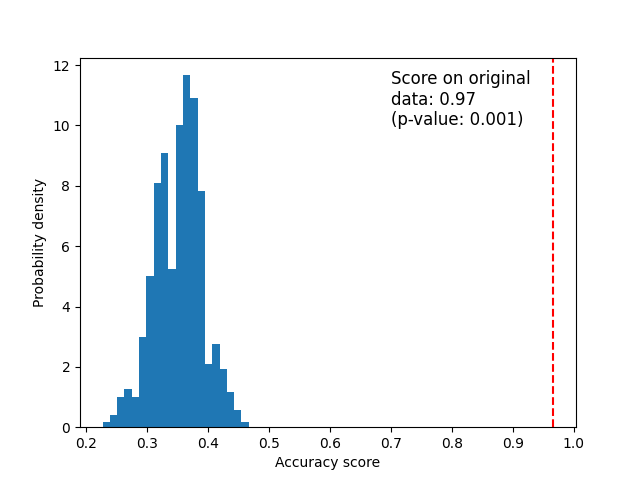
البيانات الأصلية#
أدناه نرسم مخططًا لتوزيع درجات التبديل (التوزيع الصفري). يشير الخط الأحمر إلى الدرجة التي حصل عليها المصنف على البيانات الأصلية. الدرجة أفضل بكثير من تلك التي تم الحصول عليها عن طريق استخدام البيانات المبدلة وقيمة p منخفضة جدًا. هذا يشير إلى أن هناك احتمالًا ضئيلًا للحصول على هذه الدرجة الجيدة عن طريق الصدفة وحدها. إنه يقدم دليلًا على أن مجموعة بيانات السوسن تحتوي على اعتماد حقيقي بين الميزات والعلامات وتمكن المصنف من استخدام هذا للحصول على نتائج جيدة.
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.hist(perm_scores_iris, bins=20, density=True)
ax.axvline(score_iris, ls="--", color="r")
score_label = f"Score on original\ndata: {score_iris:.2f}\n(p-value: {pvalue_iris:.3f})"
ax.text(0.7, 10, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
_ = ax.set_ylabel("Probability density")
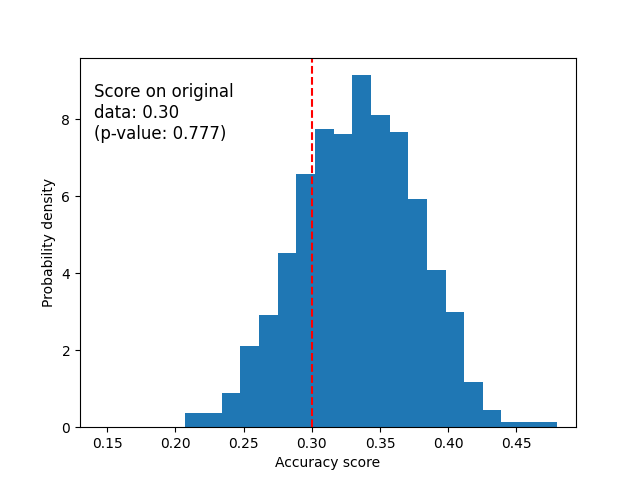
البيانات العشوائية#
أدناه نرسم التوزيع الصفري للبيانات العشوائية. درجات التبديل مشابهة لتلك التي تم الحصول عليها باستخدام مجموعة بيانات السوسن الأصلية لأن التبديل دائمًا ما يدمر أي اعتماد بين الميزة والعلامة. الدرجة المحصلة على البيانات العشوائية الأصلية في هذه الحالة، هي سيئة للغاية. يؤدي هذا إلى قيمة p كبيرة، مما يؤكد أنه لم يكن هناك اعتماد بين الميزة والعلامة في البيانات الأصلية.
fig, ax = plt.subplots()
ax.hist(perm_scores_rand, bins=20, density=True)
ax.set_xlim(0.13)
ax.axvline(score_rand, ls="--", color="r")
score_label = f"Score on original\ndata: {score_rand:.2f}\n(p-value: {pvalue_rand:.3f})"
ax.text(0.14, 7.5, score_label, fontsize=12)
ax.set_xlabel("Accuracy score")
ax.set_ylabel("Probability density")
plt.show()
سبب محتمل آخر للحصول على قيمة p عالية هو أن المصنف لم يتمكن من استخدام البنية في البيانات. في هذه الحالة، ستكون قيمة p منخفضة فقط للمصنفين القادرين على استخدام الاعتماد الموجود. في حالتنا أعلاه، حيث تكون البيانات عشوائية، سيكون لدى جميع المصنفين قيمة p عالية حيث لا توجد بنية موجودة في البيانات.
أخيرًا، لاحظ أنه تم إثبات أن هذا الاختبار ينتج قيم p منخفضة حتى إذا كان هناك بنية ضعيفة فقط في البيانات [1].
المراجع
Total running time of the script: (0 minutes 15.031 seconds)
Related examples
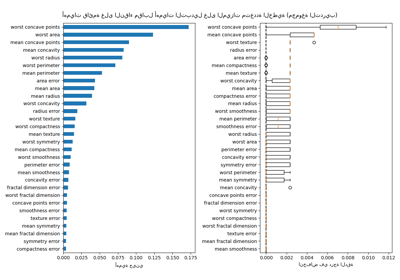
أهمية التبديل مع الميزات متعددة الخطية أو المرتبطة
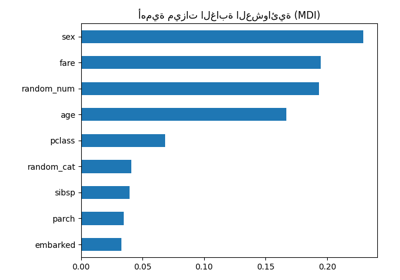
أهمية التبديل مقابل أهمية ميزة الغابة العشوائية (MDI)