ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

منحنى استقبال التشغيل متعدد الفئات (ROC)#

يصف هذا المثال استخدام مقياس استقبال التشغيل (ROC) لتقييم جودة المصنفات متعددة الفئات.

عادةً ما تتميز منحنيات ROC بمعدل الإيجابيات الحقيقية (TPR) على محور Y، ومعدل الإيجابيات الخاطئة (FPR) على محور X. وهذا يعني أن الركن العلوي الأيسر من المخطط هو النقطة "المثالية" - FPR صفر، وTPR واحد. هذا ليس واقعيًا جدًا، ولكنه يعني أن مساحة أكبر تحت المنحنى (AUC) تكون عادةً أفضل. "انحدار" منحنيات ROC مهم أيضًا، حيث أنه من المثالي تحقيق أقصى استفادة من TPR مع تقليل FPR.

تُستخدم منحنيات ROC عادةً في التصنيف الثنائي، حيث يمكن تعريف TPR وFPR بشكل لا لبس فيه. في حالة التصنيف متعدد الفئات، يتم الحصول على مفهوم TPR أو FPR فقط بعد تحويل الإخراج إلى ثنائي. يمكن القيام بذلك بطريقتين مختلفتين:

مخطط One-vs-Rest يقارن كل فئة ضد جميع الفئات الأخرى (يُفترض أنها واحدة)؛
مخطط One-vs-One يقارن كل مجموعة فريدة من المجموعات المزدوجة من الفئات.

في هذا المثال، نستكشف كلا المخططين ونعرض مفاهيم المتوسطات الدقيقة والكلية كطرق مختلفة لتلخيص معلومات منحنيات ROC متعددة الفئات.

ملاحظة

راجع منحنى المستقبل التشغيلي (ROC) مع التحقق المتقاطع للتوسع في هذا المثال وتقدير تباين منحنيات ROC وقيم AUC الخاصة بها.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

تحميل البيانات وإعدادها#

نستورد Iris plants dataset الذي يحتوي على 3 فئات، كل منها يتوافق مع نوع من نبات الزنبق. يمكن فصل فئة واحدة خطيًا عن الباقيتين؛ أما الفئتان الأخريان فلا يمكن فصلهما خطيًا عن بعضهما البعض.

هنا نقوم بتحويل الإخراج إلى ثنائي وإضافة ميزات عشوائية لجعل المشكلة أكثر صعوبة.

import numpy as np

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()
target_names = iris.target_names
X, y = iris.data, iris.target
y = iris.target_names[y]

random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
n_classes = len(np.unique(y))
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)
(
    X_train,
    X_test,
    y_train,
    y_test,
) = train_test_split(X, y, test_size=0.5, stratify=y, random_state=0)

نقوم بتدريب نموذج LogisticRegression الذي يمكنه التعامل مع المشاكل متعددة الفئات بشكل طبيعي، وذلك بفضل استخدام الصيغة متعددة الحدود.

from sklearn.linear_model import LogisticRegression

classifier = LogisticRegression()
y_score = classifier.fit(X_train, y_train).predict_proba(X_test)

منحنى استقبال التشغيل متعدد الفئات One-vs-Rest#

تتكون استراتيجية One-vs-the-Rest (OvR) متعددة الفئات، والمعروفة أيضًا as one-vs-all، من حساب منحنى ROC لكل من n_classes. في كل خطوة، يتم اعتبار فئة معينة على أنها الفئة الإيجابية، ويتم اعتبار الفئات المتبقية على أنها الفئة السلبية ككتلة واحدة.

ملاحظة

لا يجب الخلط بين استراتيجية OvR المستخدمة لتقييم المصنفات متعددة الفئات مع استراتيجية OvR المستخدمة لتدريب مصنف متعدد الفئات عن طريق ملاءمة مجموعة من المصنفات الثنائية (على سبيل المثال عبر OneVsRestClassifier meta-estimator). يمكن استخدام تقييم OvR ROC لفحص أي نوع من نماذج التصنيف بغض النظر عن كيفية تدريبها (راجع خوارزميات متعددة التصنيف ومتعددة الإخراج).

في هذا القسم، نستخدم LabelBinarizer لتحويل الهدف إلى ثنائي باستخدام الترميز one-hot-encoding بطريقة OvR. وهذا يعني أن الهدف ذو الشكل (n_samples,) يتم تعيينه إلى هدف ذو الشكل (n_samples, n_classes).

from sklearn.preprocessing import LabelBinarizer

label_binarizer = LabelBinarizer().fit(y_train)
y_onehot_test = label_binarizer.transform(y_test)
y_onehot_test.shape  # (n_samples, n_classes)

(75, 3)

يمكننا أيضًا التحقق بسهولة من ترميز فئة معينة:

label_binarizer.transform(["virginica"])

array([[0, 0, 1]])

منحنى ROC يظهر فئة معينة#

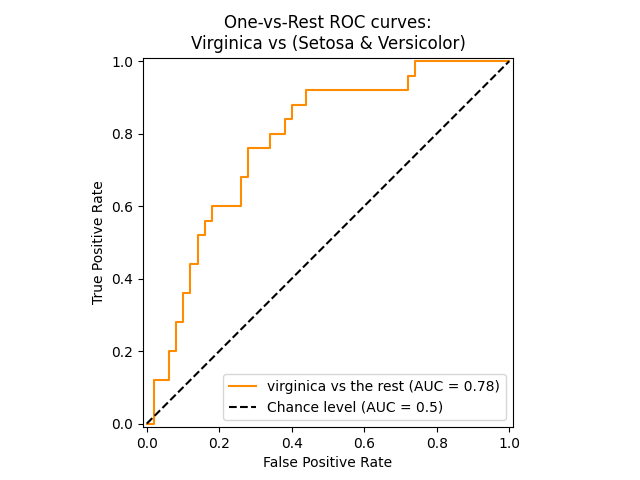
في المخطط التالي، نعرض منحنى ROC الناتج عند اعتبار أزهار الزنبق إما "virginica" (class_id=2) أو "non-virginica" (الباقي).

class_of_interest = "virginica"
class_id = np.flatnonzero(label_binarizer.classes_ == class_of_interest)[0]
class_id

np.int64(2)

import matplotlib.pyplot as plt

from sklearn.metrics import RocCurveDisplay

display = RocCurveDisplay.from_predictions(
    y_onehot_test[:, class_id],
    y_score[:, class_id],
    name=f"{class_of_interest} vs the rest",
    color="darkorange",
    plot_chance_level=True,
    # despine=True,
)
_ = display.ax_.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title="One-vs-Rest ROC curves:\nVirginica vs (Setosa & Versicolor)",
)

One-vs-Rest ROC curves: Virginica vs (Setosa & Versicolor)

منحنى ROC باستخدام المتوسط الدقيق لـ OvR#

يقوم المتوسط الدقيق بتجميع المساهمات من جميع الفئات (باستخدام numpy.ravel) لحساب متوسط المقاييس كما يلي:

\(TPR=\frac{\sum_{c}TP_c}{\sum_{c}(TP_c + FN_c)}\) ;

\(FPR=\frac{\sum_{c}FP_c}{\sum_{c}(FP_c + TN_c)}\) .

يمكننا باختصار عرض تأثير numpy.ravel:

print(f"y_score:\n{y_score[0:2,:]}")
print()
print(f"y_score.ravel():\n{y_score[0:2,:].ravel()}")

y_score:
[[0.38095776 0.05072909 0.56831315]
 [0.07031555 0.27915668 0.65052777]]

y_score.ravel():
[0.38095776 0.05072909 0.56831315 0.07031555 0.27915668 0.65052777]

في إعداد التصنيف متعدد الفئات مع الفئات غير المتوازنة للغاية، يفضل المتوسط الدقيق على المتوسط الكلي. في مثل هذه الحالات، يمكن للمرء أن يستخدم المتوسط الكلي المرجح، والذي لم يتم عرضه هنا.

display = RocCurveDisplay.from_predictions(
    y_onehot_test.ravel(),
    y_score.ravel(),
    name="micro-average OvR",
    color="darkorange",
    plot_chance_level=True,
    # despine=True,
)
_ = display.ax_.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title="Micro-averaged One-vs-Rest\nReceiver Operating Characteristic",
)

Micro-averaged One-vs-Rest Receiver Operating Characteristic

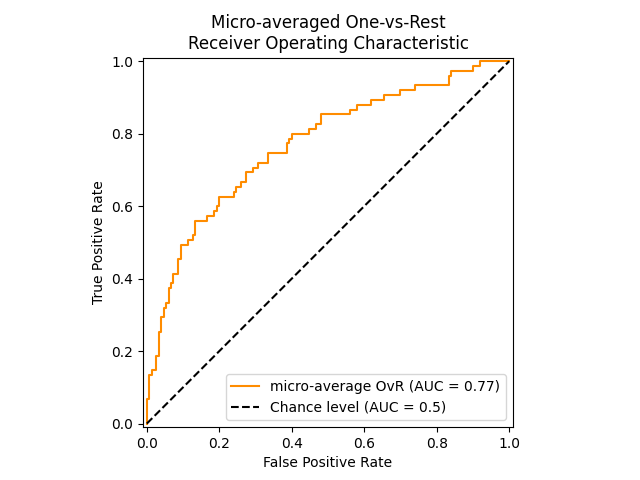
في الحالة التي يكون فيها الاهتمام الرئيسي ليس بالمخطط ولكن بقيمة ROC-AUC نفسها، يمكننا إعادة إنتاج القيمة المعروضة في المخطط باستخدام roc_auc_score.

from sklearn.metrics import roc_auc_score

micro_roc_auc_ovr = roc_auc_score(
    y_test,
    y_score,
    multi_class="ovr",
    average="micro",
)

print(f"Micro-averaged One-vs-Rest ROC AUC score:\n{micro_roc_auc_ovr:.2f}")

Micro-averaged One-vs-Rest ROC AUC score:
0.77

هذا يعادل حساب منحنى ROC باستخدام roc_curve ثم حساب المساحة تحت المنحنى باستخدام auc للفئات الحقيقية والمتوقعة المبسطة.

from sklearn.metrics import auc, roc_curve

# تخزين fpr, tpr, و roc_auc لجميع استراتيجيات المتوسط
fpr, tpr, roc_auc = dict(), dict(), dict()
# حساب منحنى ROC المتوسط الدقيق والمساحة تحت المنحنى
fpr["micro"], tpr["micro"], _ = roc_curve(y_onehot_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

print(f"Micro-averaged One-vs-Rest ROC AUC score:\n{roc_auc['micro']:.2f}")

Micro-averaged One-vs-Rest ROC AUC score:
0.77

ملاحظة

بشكل افتراضي، يقوم حساب منحنى ROC بإضافة نقطة واحدة عند أقصى معدل إيجابيات خاطئة باستخدام الاستيفاء الخطي وتصحيح McClish [Analyzing a portion of the ROC curve Med Decis Making. 1989 Jul-Sep; 9(3):190-5.].

منحنى ROC باستخدام المتوسط الكلي لـ OvR#

يتطلب الحصول على المتوسط الكلي حساب المقياس بشكل مستقل لكل فئة ثم أخذ المتوسط عبرها، وبالتالي معاملة جميع الفئات بشكل متساوٍ مسبقًا. نقوم أولاً بتجميع معدلات الإيجابيات الحقيقية/الخاطئة لكل فئة:

for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_onehot_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

fpr_grid = np.linspace(0.0, 1.0, 1000)

# استيفاء جميع منحنيات ROC عند هذه النقاط
mean_tpr = np.zeros_like(fpr_grid)

for i in range(n_classes):
    mean_tpr += np.interp(fpr_grid, fpr[i], tpr[i])  # الاستيفاء الخطي

# حساب المتوسط وحساب AUC
mean_tpr /= n_classes

fpr["macro"] = fpr_grid
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])

print(f"Macro-averaged One-vs-Rest ROC AUC score:\n{roc_auc['macro']:.2f}")

Macro-averaged One-vs-Rest ROC AUC score:
0.78

هذا الحساب يعادل ببساطة استدعاء

macro_roc_auc_ovr = roc_auc_score(
    y_test,
    y_score,
    multi_class="ovr",
    average="macro",
)

print(f"Macro-averaged One-vs-Rest ROC AUC score:\n{macro_roc_auc_ovr:.2f}")

Macro-averaged One-vs-Rest ROC AUC score:
0.78

رسم جميع منحنيات OvR ROC معًا#

from itertools import cycle

fig, ax = plt.subplots(figsize=(6, 6))

plt.plot(
    fpr["micro"],
    tpr["micro"],
    label=f"micro-average ROC curve (AUC = {roc_auc['micro']:.2f})",
    color="deeppink",
    linestyle=":",
    linewidth=4,
)

plt.plot(
    fpr["macro"],
    tpr["macro"],
    label=f"macro-average ROC curve (AUC = {roc_auc['macro']:.2f})",
    color="navy",
    linestyle=":",
    linewidth=4,
)

colors = cycle(["aqua", "darkorange", "cornflowerblue"])
for class_id, color in zip(range(n_classes), colors):
    RocCurveDisplay.from_predictions(
        y_onehot_test[:, class_id],
        y_score[:, class_id],
        name=f"ROC curve for {target_names[class_id]}",
        color=color,
        ax=ax,
        plot_chance_level=(class_id == 2),
        # despine=True,
    )

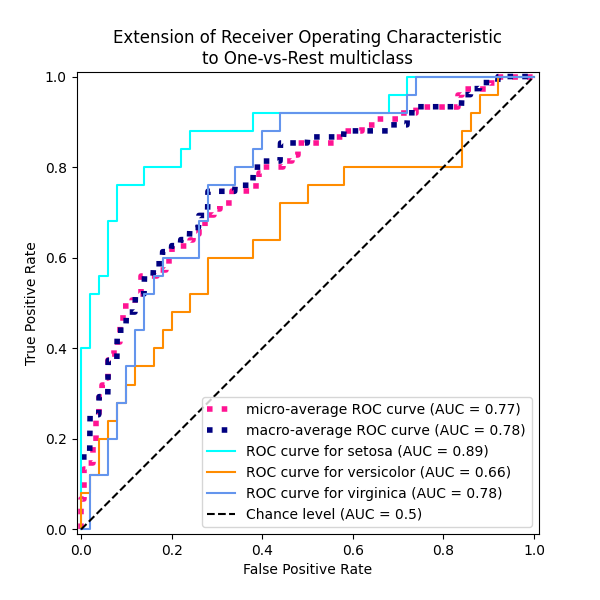
_ = ax.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title="Extension of Receiver Operating Characteristic\nto One-vs-Rest multiclass",
)

Extension of Receiver Operating Characteristic to One-vs-Rest multiclass

منحنى استقبال التشغيل متعدد الفئات One-vs-One#

تتكون استراتيجية One-vs-One (OvO) متعددة الفئات من ملاءمة مصنف واحد لكل زوج من الفئات. نظرًا لأنه يتطلب تدريب n_classes * (n_classes - 1) / 2 من المصنفات، فإن هذه الطريقة تكون عادةً أبطأ من One-vs-Rest بسبب تعقيدها O(n_classes ^2).

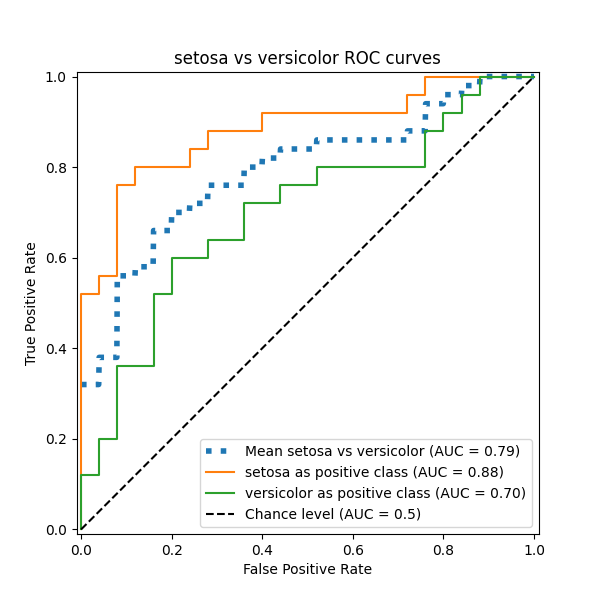
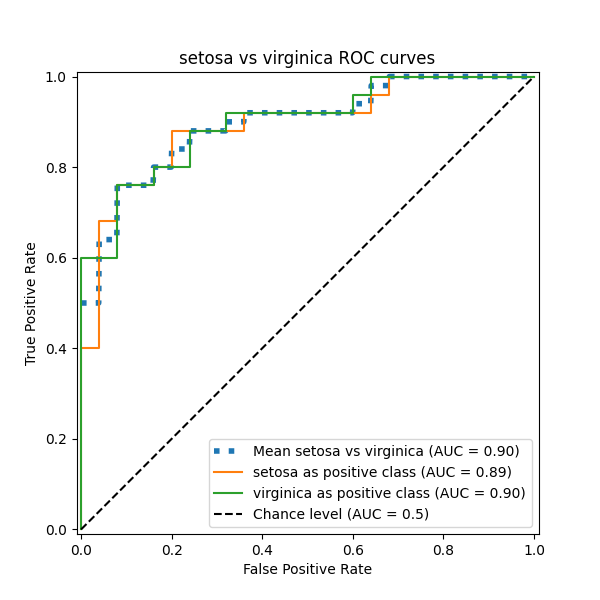
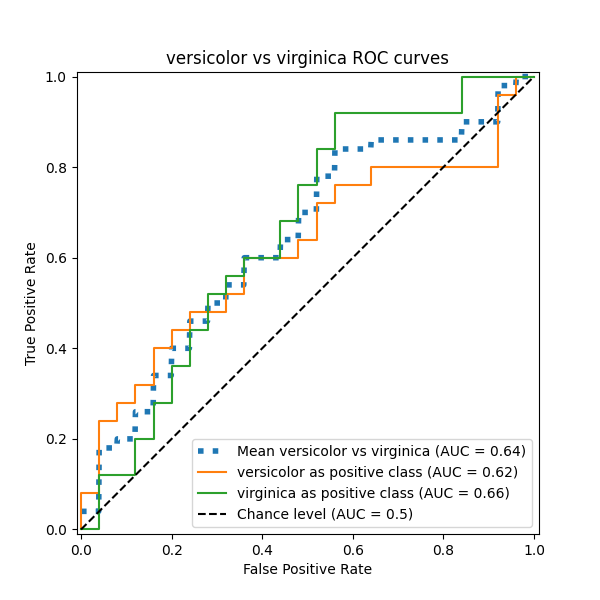
في هذا القسم، نعرض المتوسط الكلي لـ AUC باستخدام مخطط OvO للمجموعات الثلاث الممكنة في Iris plants dataset: "setosa" vs "versicolor"، و"versicolor" vs "virginica"، و"virginica" vs "setosa". لاحظ أن المتوسط الدقيق غير محدد لمخطط OvO.

منحنى ROC باستخدام المتوسط الكلي لـ OvO#

في مخطط OvO، تتمثل الخطوة الأولى في تحديد جميع المجموعات الفريدة الممكنة من الأزواج. يتم حساب الدرجات عن طريق معاملة أحد العناصر في زوج معين على أنه الفئة الإيجابية والعنصر الآخر على أنه الفئة السلبية، ثم إعادة حساب الدرجة عن طريق عكس الأدوار وأخذ متوسط الدرجتين.

from itertools import combinations

pair_list = list(combinations(np.unique(y), 2))
print(pair_list)

[(np.str_('setosa'), np.str_('versicolor')), (np.str_('setosa'), np.str_('virginica')), (np.str_('versicolor'), np.str_('virginica'))]

pair_scores = []
mean_tpr = dict()

for ix, (label_a, label_b) in enumerate(pair_list):
    a_mask = y_test == label_a
    b_mask = y_test == label_b
    ab_mask = np.logical_or(a_mask, b_mask)

    a_true = a_mask[ab_mask]
    b_true = b_mask[ab_mask]

    idx_a = np.flatnonzero(label_binarizer.classes_ == label_a)[0]
    idx_b = np.flatnonzero(label_binarizer.classes_ == label_b)[0]

    fpr_a, tpr_a, _ = roc_curve(a_true, y_score[ab_mask, idx_a])
    fpr_b, tpr_b, _ = roc_curve(b_true, y_score[ab_mask, idx_b])

    mean_tpr[ix] = np.zeros_like(fpr_grid)
    mean_tpr[ix] += np.interp(fpr_grid, fpr_a, tpr_a)
    mean_tpr[ix] += np.interp(fpr_grid, fpr_b, tpr_b)
    mean_tpr[ix] /= 2
    mean_score = auc(fpr_grid, mean_tpr[ix])
    pair_scores.append(mean_score)

    fig, ax = plt.subplots(figsize=(6, 6))
    plt.plot(
        fpr_grid,
        mean_tpr[ix],
        label=f"Mean {label_a} vs {label_b} (AUC = {mean_score :.2f})",
        linestyle=":",
        linewidth=4,
    )
    RocCurveDisplay.from_predictions(
        a_true,
        y_score[ab_mask, idx_a],
        ax=ax,
        name=f"{label_a} as positive class",
    )
    RocCurveDisplay.from_predictions(
        b_true,
        y_score[ab_mask, idx_b],
        ax=ax,
        name=f"{label_b} as positive class",
        plot_chance_level=True,
        # despine=True,
    )
    ax.set(
        xlabel="False Positive Rate",
        ylabel="True Positive Rate",
        title=f"{target_names[idx_a]} vs {label_b} ROC curves",
    )

print(f"Macro-averaged One-vs-One ROC AUC score:\n{np.average(pair_scores):.2f}")

Macro-averaged One-vs-One ROC AUC score:
0.78

يمكن للمرء أيضًا التأكيد على أن المتوسط الكلي الذي حسبناه "يدويًا" مكافئ لخيار average="macro" المطبق في دالة roc_auc_score.

macro_roc_auc_ovo = roc_auc_score(
    y_test,
    y_score,
    multi_class="ovo",
    average="macro",
)

print(f"درجة متوسط One-vs-One ROC AUC الكلي:\n{macro_roc_auc_ovo:.2f}")

درجة متوسط One-vs-One ROC AUC الكلي:
0.78

رسم جميع منحنيات OvO ROC معًا#

ovo_tpr = np.zeros_like(fpr_grid)

fig, ax = plt.subplots(figsize=(6, 6))
for ix, (label_a, label_b) in enumerate(pair_list):
    ovo_tpr += mean_tpr[ix]
    ax.plot(
        fpr_grid,
        mean_tpr[ix],
        label=f"متوسط {label_a} مقابل {label_b} (AUC = {pair_scores[ix]:.2f})",
    )

ovo_tpr /= sum(1 for pair in enumerate(pair_list))

ax.plot(
    fpr_grid,
    ovo_tpr,
    label=f"One-vs-One متوسط كلي (AUC = {macro_roc_auc_ovo:.2f})",
    linestyle=":",
    linewidth=4,
)
ax.plot([0, 1], [0, 1], "k--", label="مستوى الصدفة (AUC = 0.5)")
_ = ax.set(
    xlabel="معدل الإيجابيات الخاطئة",
    ylabel="معدل الإيجابيات الحقيقية",
    title="تمديد خاصية تشغيل المستقبل\nإلى One-vs-One متعدد الفئات",
    aspect="equal",
    xlim=(-0.01, 1.01),
    ylim=(-0.01, 1.01),
)

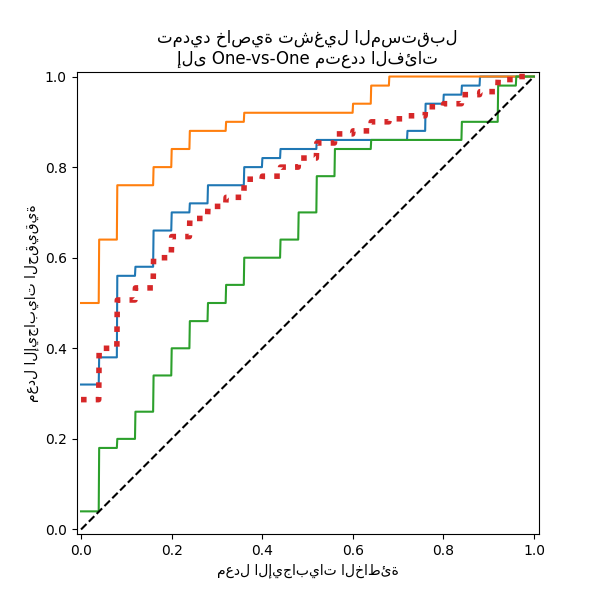
تمديد خاصية تشغيل المستقبل إلى One-vs-One متعدد الفئات

نؤكد أن الفئتين "versicolor" و "virginica" غير محددتين جيدًا بواسطة مصنف خطي. لاحظ أن درجة "virginica"-مقابل-البقية ROC-AUC (0.77) تقع بين درجات OvO ROC-AUC لـ "versicolor" مقابل "virginica" (0.64) و "setosa" مقابل "virginica" (0.90). في الواقع، تعطي استراتيجية OvO معلومات إضافية حول الالتباس بين زوج من الفئات، على حساب التكلفة الحسابية عندما يكون عدد الفئات كبيرًا.

يوصى باستخدام استراتيجية OvO إذا كان المستخدم مهتمًا بشكل أساسي بتحديد فئة معينة أو مجموعة فرعية من الفئات بشكل صحيح، بينما يمكن تلخيص التقييم الشامل لأداء المصنف من خلال استراتيجية متوسط محددة.

متوسط OvR ROC الجزئي يهيمن عليه الفئة الأكثر تكرارًا، حيث يتم تجميع التهم. يعكس البديل المتوسط الكلي إحصائيات الفئات الأقل تكرارًا بشكل أفضل، ومن ثم يكون أكثر ملاءمة عندما يعتبر الأداء في جميع الفئات ذا أهمية متساوية.

Total running time of the script: (0 minutes 0.701 seconds)