ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

عرض توضيحي لخوارزمية التجميع DBSCAN#

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) يجد العينات الأساسية في مناطق ذات كثافة عالية ويوسع التجمعات منها. هذا الخوارزم جيد للبيانات التي تحتوي على تجمعات ذات كثافة مماثلة.

راجع مثال مقارنة خوارزميات التجميع المختلفة على مجموعات البيانات التجريبية لعرض توضيحي لخوارزميات تجميع مختلفة على مجموعات بيانات ثنائية الأبعاد.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

توليد البيانات#

نستخدم make_blobs لإنشاء 3 مجموعات صناعية.

from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler

centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(
    n_samples=750, centers=centers, cluster_std=0.4, random_state=0
)

X = StandardScaler().fit_transform(X)

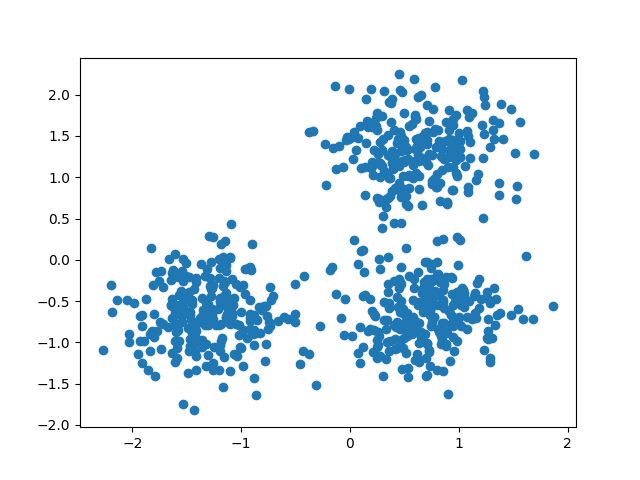
يمكننا تصور البيانات الناتجة:

import matplotlib.pyplot as plt

plt.scatter(X[:, 0], X[:, 1])
plt.show()

حساب DBSCAN#

يمكن الوصول إلى العلامات التي تم تعيينها بواسطة DBSCAN باستخدام سمة labels_. يتم إعطاء العينات الضجيجية التسمية math:-1.

import numpy as np

from sklearn import metrics
from sklearn.cluster import DBSCAN

db = DBSCAN(eps=0.3, min_samples=10).fit(X)
labels = db.labels_

# عدد التجمعات في العلامات، مع تجاهل الضجيج إذا كان موجودًا.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)

print("Estimated number of clusters: %d" % n_clusters_)
print("Estimated number of noise points: %d" % n_noise_)

Estimated number of clusters: 3
Estimated number of noise points: 18

خوارزميات التجميع هي أساليب تعلم غير خاضعة للإشراف بشكل أساسي. ومع ذلك، نظرًا لأن make_blobs يتيح الوصول إلى العلامات الحقيقية للتجمعات الاصطناعية، فمن الممكن استخدام مقاييس التقييم التي تستفيد من معلومات "الإشراف" هذه لتقييم جودة التجمعات الناتجة. أمثلة على هذه المقاييس هي التجانس، والاكتمال، وV-measure، وRand-Index، وAdjusted Rand-Index، وAdjusted Mutual Information (AMI).

إذا لم تكن العلامات الحقيقية معروفة، يمكن إجراء التقييم باستخدام نتائج النموذج نفسه فقط. في هذه الحالة، يأتي معامل Silhouette Coefficient في متناول اليد.

لمزيد من المعلومات، راجع تعديل الفرصة في تقييم أداء التجميع المثال أو الوحدة النمطية تقييم أداء التجميع.

print(f"Homogeneity: {metrics.homogeneity_score(labels_true, labels):.3f}")
print(f"Completeness: {metrics.completeness_score(labels_true, labels):.3f}")
print(f"V-measure: {metrics.v_measure_score(labels_true, labels):.3f}")
print(f"Adjusted Rand Index: {metrics.adjusted_rand_score(labels_true, labels):.3f}")
print(
    "Adjusted Mutual Information:"
    f" {metrics.adjusted_mutual_info_score(labels_true, labels):.3f}"
)
print(f"Silhouette Coefficient: {metrics.silhouette_score(X, labels):.3f}")

Homogeneity: 0.953
Completeness: 0.883
V-measure: 0.917
Adjusted Rand Index: 0.952
Adjusted Mutual Information: 0.916
Silhouette Coefficient: 0.626

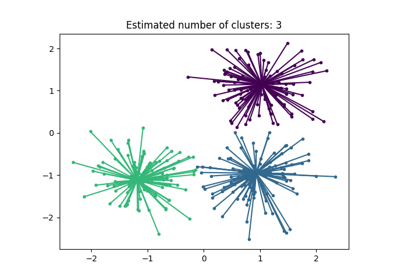
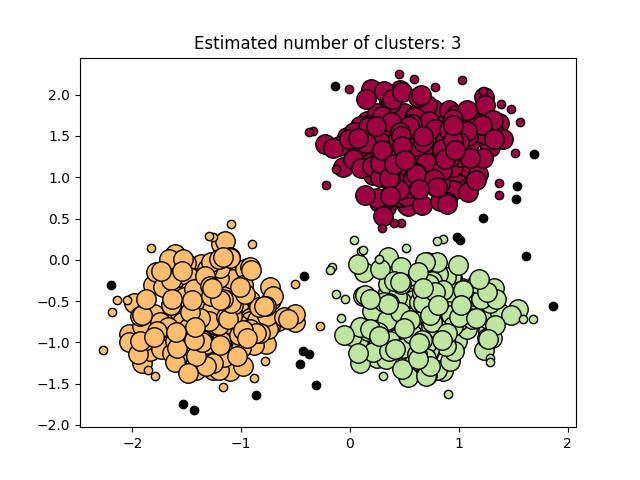
عرض النتائج#

يتم ترميز العينات الأساسية (النقاط الكبيرة) والعينات غير الأساسية (النقاط الصغيرة) بالألوان وفقًا للتجمع المعين. يتم تمثيل العينات الموسومة كضجيج باللون الأسود.

unique_labels = set(labels)
core_samples_mask = np.zeros_like(labels, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True

colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = labels == k

    xy = X[class_member_mask & core_samples_mask]
    plt.plot(
        xy[:, 0],
        xy[:, 1],
        "o",
        markerfacecolor=tuple(col),
        markeredgecolor="k",
        markersize=14,
    )

    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(
        xy[:, 0],
        xy[:, 1],
        "o",
        markerfacecolor=tuple(col),
        markeredgecolor="k",
        markersize=6,
    )
plt.title(f"Estimated number of clusters: {n_clusters_}")
plt.show()