ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

معاملات Ridge كدالة لتنظيم L2#

النموذج الذي يبالغ في التعميم يتعلم بيانات التدريب جيدًا جدًا، حيث يلتقط كل من الأنماط الأساسية والضوضاء في البيانات. ومع ذلك، عند تطبيقه على بيانات غير معروفة، قد لا تستمر الارتباطات المكتسبة. عادة ما نكتشف ذلك عندما نطبق تنبؤاتنا المدربة على بيانات الاختبار ونرى الأداء الإحصائي ينخفض بشكل كبير مقارنة ببيانات التدريب.

تتمثل إحدى طرق التغلب على المبالغة في التعميم في التنظيم، والذي يمكن القيام به عن طريق معاقبة الأوزان الكبيرة (المعاملات) في النماذج الخطية، مما يجبر النموذج على تقلص جميع المعاملات. يقلل التنظيم من اعتماد النموذج على معلومات محددة تم الحصول عليها من عينات التدريب.

يوضح هذا المثال كيف يؤثر التنظيم L2 في Ridge الانحدار على أداء النموذج من خلال إضافة مصطلح عقوبة إلى الخسارة التي تزداد مع المعاملات \(\beta\).

دالة الخسارة المنظمة تعطى بواسطة: \(\mathcal{L}(X, y, \beta) = \| y - X \beta \|^{2}_{2} + \alpha \| \beta \|^{2}_{2}\)

حيث \(X\) هي بيانات الإدخال، \(y\) هي المتغير المستهدف، \(\beta\) هو متجه المعاملات المرتبطة بالميزات، و \(\alpha\) هو قوة التنظيم.

تهدف دالة الخسارة المنظمة إلى تحقيق التوازن بين المقايضة بين التنبؤ بدقة بمجموعة التدريب ومنع المبالغة في التعميم.

في هذه الخسارة المنظمة، الجانب الأيسر (على سبيل المثال \(\|y - X\beta\|^{2}_{2}\)) يقيس الفرق التربيعي بين المتغير المستهدف الفعلي، \(y\)، والقيم المتوقعة. يمكن أن يؤدي تقليل هذا المصطلح وحده إلى المبالغة في التعميم، حيث قد يصبح النموذج معقدًا وحساسًا للضوضاء في بيانات التدريب.

للتغلب على المبالغة في التعميم، يضيف تنظيم Ridge قيدًا، يسمى مصطلح العقوبة، (\(\alpha \| \beta\|^{2}_{2}\)) إلى دالة الخسارة. هذا المصطلح العقابي هو مجموع مربعات معاملات النموذج، مضروبًا في قوة التنظيم \(\alpha\). من خلال تقديم هذا القيد، يثبط تنظيم Ridge أي معامل فردي \(\beta_{i}\) من اتخاذ قيمة كبيرة بشكل مفرط ويشجع المعاملات الأصغر والأكثر توزيعًا بالتساوي. تجبر القيم الأعلى من \(\alpha\) المعاملات على الصفر. ومع ذلك، يمكن أن يؤدي \(\alpha\) المرتفع بشكل مفرط إلى نموذج غير مناسب يفشل في التقاط الأنماط المهمة في البيانات.

لذلك، تجمع دالة الخسارة المنظمة بين مصطلح دقة التنبؤ ومصطلح العقوبة. من خلال ضبط قوة التنظيم، يمكن للممارسين ضبط درجة القيد المفروض على الأوزان، وتدريب نموذج قادر على التعميم بشكل جيد على بيانات غير معروفة مع تجنب المبالغة في التعميم.

# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause

الغرض من هذا المثال#

لغرض إظهار كيفية عمل التنظيم Ridge، سنقوم بإنشاء مجموعة بيانات غير ضوضائية. ثم سنقوم بتدريب نموذج منظم على نطاق من قيم التنظيم (\(\alpha\)) ونرسم كيف أن المعاملات المدربة ومتوسط الخطأ التربيعي بين تلك والقيم الأصلية تتصرف كدالة لقوة التنظيم.

إنشاء مجموعة بيانات غير ضوضائية#

نقوم بإنشاء مجموعة بيانات تجريبية بها 100 عينة و10 ميزات، وهي مناسبة للكشف عن الانحدار. من بين 10 ميزات، 8 منها مفيدة وتساهم في الانحدار، في حين أن الميزتين المتبقيتين ليس لهما أي تأثير على المتغير المستهدف (معاملاتها الحقيقية هي 0). يرجى ملاحظة أنه في هذا المثال، البيانات غير ضوضائية، وبالتالي يمكننا توقع نموذج الانحدار الخاص بنا لاستعادة المعاملات الحقيقية بالضبط w.

from sklearn.datasets import make_regression

X, y, w = make_regression(
    n_samples=100, n_features=10, n_informative=8, coef=True, random_state=1
)

# الحصول على المعاملات الحقيقية
print(f"معامل الانحدار الحقيقي لهذه المشكلة هو:\n{w}")

معامل الانحدار الحقيقي لهذه المشكلة هو:
[38.32634568 88.49665188  0.         29.75747153  0.         19.08699432
 25.44381023 38.69892343 49.28808734 71.75949622]

تدريب منظم الانحدار#

نستخدم Ridge، وهو نموذج خطي مع L2 التنظيم. نقوم بتدريب عدة نماذج، كل منها بقيمة مختلفة لـ معلمة النموذج alpha، وهي ثابتة إيجابية تضرب مصطلح العقوبة، مما يتحكم في قوة التنظيم. بالنسبة لكل نموذج مدرب ثم نحسب الخطأ بين المعاملات الحقيقية w و المعاملات التي وجدها النموذج clf. نقوم بتخزين المعاملات المحددة والأخطاء المحسوبة للمعاملات المقابلة في القوائم، مما يجعل من الملائم لنا رسمها.

import numpy as np

from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error

clf = Ridge()

# توليد قيم لـ `alpha` موزعة بالتساوي على مقياس لوغاريتمي
alphas = np.logspace(-3, 4, 200)
coefs = []
errors_coefs = []

# تدريب النموذج بقيم تنظيم مختلفة
for a in alphas:
    clf.set_params(alpha=a).fit(X, y)
    coefs.append(clf.coef_)
    errors_coefs.append(mean_squared_error(clf.coef_, w))

رسم المعاملات المدربة ومتوسط الخطأ التربيعي#

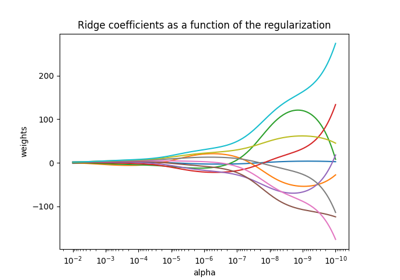
نرسم الآن 10 معاملات منظمة مختلفة كدالة لـ معلمة التنظيم alpha حيث يمثل كل لون معاملًا مختلفًا.

على الجانب الأيمن، نرسم كيف تتغير أخطاء المعاملات من المقدر كدالة للتنظيم.

import matplotlib.pyplot as plt
import pandas as pd

alphas = pd.Index(alphas, name="alpha")
coefs = pd.DataFrame(coefs, index=alphas, columns=[f"Feature {i}" for i in range(10)])
errors = pd.Series(errors_coefs, index=alphas, name="Mean squared error")

fig, axs = plt.subplots(1, 2, figsize=(20, 6))

coefs.plot(
    ax=axs[0],
    logx=True,
    title="معاملات Ridge كدالة لقوة التنظيم",
)
axs[0].set_ylabel("قيم معاملات Ridge")
errors.plot(
    ax=axs[1],
    logx=True,
    title="خطأ المعامل كدالة لقوة التنظيم",
)
_ = axs[1].set_ylabel("متوسط ​​الخطأ التربيعي")

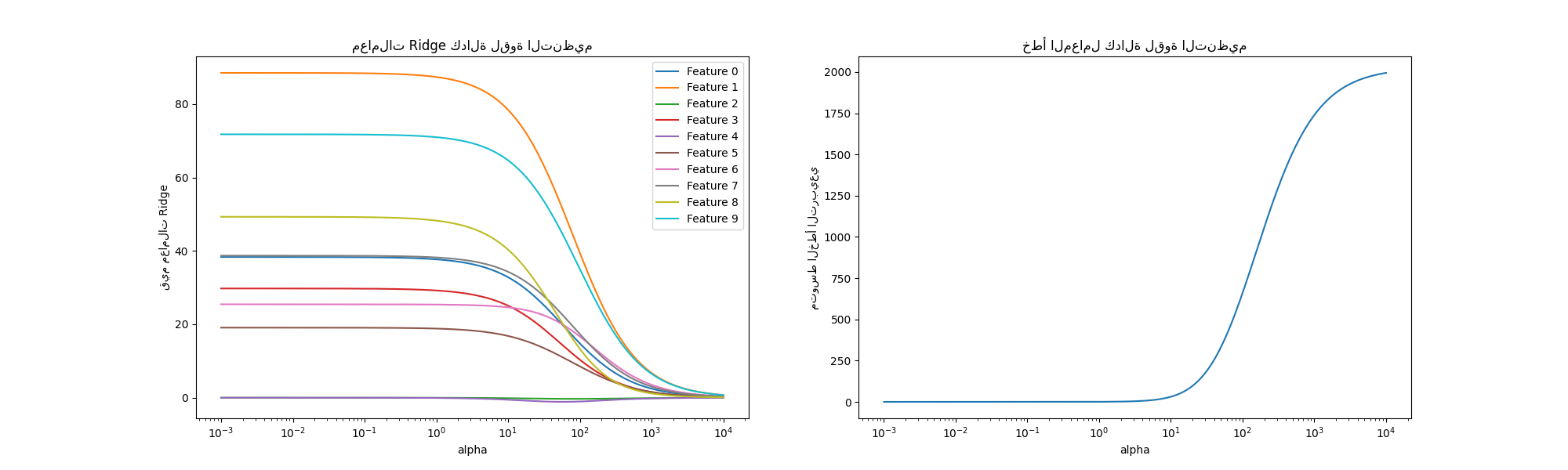
معاملات Ridge كدالة لقوة التنظيم, خطأ المعامل كدالة لقوة التنظيم

تفسير الرسوم البيانية#

يوضح الرسم البياني على الجانب الأيسر كيف تؤثر قوة التنظيم (alpha) على معاملات الانحدار Ridge. تسمح قيم alpha الأصغر (التنظيم الضعيف)، للمعاملات أن تشبه المعاملات الحقيقية (w) المستخدمة لتوليد مجموعة البيانات. هذا لأن لم يتم إضافة أي ضوضاء إضافية إلى مجموعة البيانات الاصطناعية الخاصة بنا. مع زيادة alpha، تتقلص المعاملات نحو الصفر، مما يقلل تدريجياً من تأثير الميزات التي كانت أكثر أهمية سابقًا.

يظهر الرسم البياني على الجانب الأيمن الخطأ التربيعي المتوسط (MSE) بين المعاملات التي وجدها النموذج والمعاملات الحقيقية (w). يوفر مقياسًا يتعلق بمدى دقة نموذجنا Ridge مقارنة بنموذج التوليد الحقيقي. يعني الخطأ المنخفض أن النموذج وجد معاملات أقرب إلى تلك الخاصة بنموذج التوليد الحقيقي. في هذه الحالة، نظرًا لأن مجموعة البيانات التجريبية الخاصة بنا كانت غير ضوضائية، يمكننا أن نرى أن النموذج الأقل تنظيمًا يسترد المعاملات الأقرب إلى المعاملات الحقيقية (w) (الخطأ قريب من 0).

عندما يكون alpha صغيرًا، يلتقط النموذج التفاصيل الدقيقة لبيانات التدريب، سواء كانت بسبب الضوضاء أو بسبب المعلومات الفعلية. مع زيادة alpha، تتقلص المعاملات الأعلى بسرعة أكبر، مما يجعل ميزاتها المقابلة أقل تأثيرًا في عملية التدريب. يمكن أن يعزز هذا قدرة النموذج على التعميم على بيانات غير معروفة (إذا كان هناك الكثير من الضوضاء للالتقاط)، ولكنه يفرض أيضًا خطر فقدان الأداء إذا أصبح التنظيم قويًا جدًا مقارنة بكمية الضوضاء التي تحتويها البيانات (كما في هذا المثال).

في السيناريوهات الواقعية حيث تحتوي البيانات عادةً على ضوضاء، يصبح اختيار قيمة alpha المناسبة أمرًا بالغ الأهمية في تحقيق التوازن بين نموذج المبالغة في التعميم ونموذج غير مناسب.

هنا، رأينا أن Ridge يضيف عقوبة على المعاملات لمكافحة المبالغة في التعميم. هناك مشكلة أخرى تحدث ترتبط بوجود قيم شاذة في مجموعة بيانات التدريب. القيمة الشاذة هي نقطة بيانات تختلف بشكل كبير عن الملاحظات الأخرى. بشكل ملموس، تؤثر هذه القيم الشاذة على المصطلح الموجود على الجانب الأيسر من دالة الخسارة التي أظهرناها سابقًا. بعض النماذج الخطية الأخرى مصممة لتكون قوية ضد القيم الشاذة مثل HuberRegressor. يمكنك معرفة المزيد عنها في مثال مقارنة بين HuberRegressor و Ridge على مجموعة بيانات تحتوي على قيم شاذة قوية.

Total running time of the script: (0 minutes 0.808 seconds)