ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
تأثير تغيير العتبة في التدريب الذاتي#
يوضح هذا المثال تأثير تغيير العتبة على التدريب الذاتي.
يتم تحميل مجموعة بيانات breast_cancer، ويتم حذف التصنيفات بحيث يكون 50
عينة فقط من أصل 569 عينة لديها تصنيفات. يتم تثبيت SelfTrainingClassifier على هذه
مجموعة البيانات، مع عتبات مختلفة.
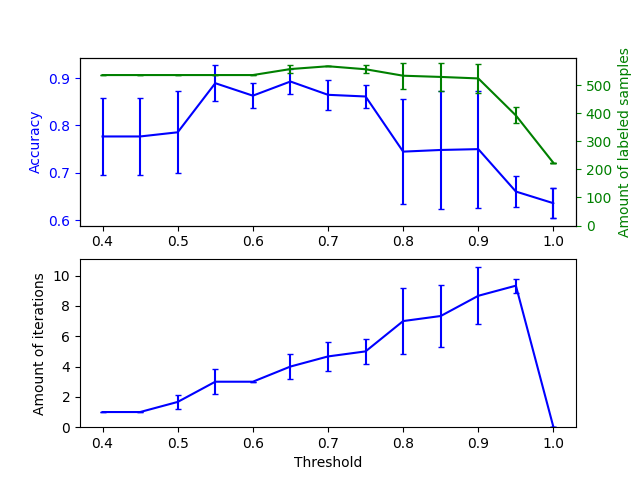
يوضح الرسم البياني العلوي كمية العينات المصنفة التي يمتلكها المصنف في نهاية التثبيت، ودقة المصنف. يوضح الرسم البياني السفلي آخر تكرار تم فيه تصنيف عينة. جميع القيم تم التحقق من صحتها عبر 3 طيات.
عند العتبات المنخفضة (في [0.4, 0.5])، يتعلم المصنف من العينات التي تم تصنيفها بثقة منخفضة. من المحتمل أن تكون هذه العينات منخفضة الثقة لديها تصنيفات متوقعة غير صحيحة، ونتيجة لذلك، فإن التثبيت على هذه التصنيفات غير الصحيحة ينتج عنه دقة ضعيفة. لاحظ أن المصنف يصنف جميع العينات تقريبًا، ويأخذ تكرارًا واحدًا فقط.
بالنسبة للعتبات العالية جدًا (في [0.9, 1)) نلاحظ أن المصنف لا يزيد من مجموعة بياناته (كمية العينات ذاتية التصنيف هي 0). ونتيجة لذلك، فإن الدقة التي تم تحقيقها بعتبة 0.9999 هي نفسها التي سيحققها المصنف المشرف العادي.
تقع الدقة المثلى بين هذين الحدين عند عتبة تبلغ حوالي 0.7.
# المؤلفون: مطوري scikit-learn
# معرف الترخيص: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.model_selection import StratifiedKFold
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC
from sklearn.utils import shuffle
n_splits = 3
X, y = datasets.load_breast_cancer(return_X_y=True)
X, y = shuffle(X, y, random_state=42)
y_true = y.copy()
y[50:] = -1
total_samples = y.shape[0]
base_classifier = SVC(probability=True, gamma=0.001, random_state=42)
x_values = np.arange(0.4, 1.05, 0.05)
x_values = np.append(x_values, 0.99999)
scores = np.empty((x_values.shape[0], n_splits))
amount_labeled = np.empty((x_values.shape[0], n_splits))
amount_iterations = np.empty((x_values.shape[0], n_splits))
for i, threshold in enumerate(x_values):
self_training_clf = SelfTrainingClassifier(base_classifier, threshold=threshold)
# نحتاج إلى التحقق اليدوي من الصحة بحيث لا نعامل -1 كفئة منفصلة
# عند حساب الدقة
skfolds = StratifiedKFold(n_splits=n_splits)
for fold, (train_index, test_index) in enumerate(skfolds.split(X, y)):
X_train = X[train_index]
y_train = y[train_index]
X_test = X[test_index]
y_test = y[test_index]
y_test_true = y_true[test_index]
self_training_clf.fit(X_train, y_train)
# كمية العينات المصنفة في نهاية التثبيت
amount_labeled[i, fold] = (
total_samples
- np.unique(self_training_clf.labeled_iter_, return_counts=True)[1][0]
)
# آخر تكرار قام فيه المصنف بتصنيف عينة
amount_iterations[i, fold] = np.max(self_training_clf.labeled_iter_)
y_pred = self_training_clf.predict(X_test)
scores[i, fold] = accuracy_score(y_test_true, y_pred)
ax1 = plt.subplot(211)
ax1.errorbar(
x_values, scores.mean(axis=1), yerr=scores.std(axis=1), capsize=2, color="b"
)
ax1.set_ylabel("Accuracy", color="b")
ax1.tick_params("y", colors="b")
ax2 = ax1.twinx()
ax2.errorbar(
x_values,
amount_labeled.mean(axis=1),
yerr=amount_labeled.std(axis=1),
capsize=2,
color="g",
)
ax2.set_ylim(bottom=0)
ax2.set_ylabel("Amount of labeled samples", color="g")
ax2.tick_params("y", colors="g")
ax3 = plt.subplot(212, sharex=ax1)
ax3.errorbar(
x_values,
amount_iterations.mean(axis=1),
yerr=amount_iterations.std(axis=1),
capsize=2,
color="b",
)
ax3.set_ylim(bottom=0)
ax3.set_ylabel("Amount of iterations")
ax3.set_xlabel("Threshold")
plt.show()
Total running time of the script: (0 minutes 5.426 seconds)
Related examples
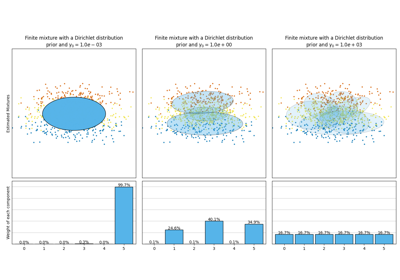
تحليل نوع أولوية التركيز لخوارزمية التباين بايزي غاوسي ميكسشر
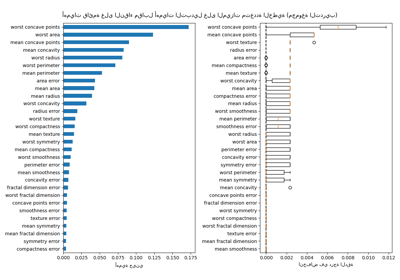
أهمية التبديل مع الميزات متعددة الخطية أو المرتبطة