ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
رسم حدود التصنيف مع نوى SVM مختلفة#
هذا المثال يوضح كيف تؤثر النوى المختلفة في SVC (دعم ناقل التصنيف) على حدود التصنيف في مشكلة تصنيف ثنائية الأبعاد.
تهدف SVCs إلى إيجاد مستوى فاصل فعال يفصل بين الفئات في بيانات التدريب الخاصة بها عن طريق زيادة الهامش بين نقاط البيانات الخارجية لكل فئة. يتم تحقيق ذلك من خلال إيجاد أفضل متجه وزن \(w\) الذي يحدد مستوى فاصل قرار المستوى الفاصل ويقلل من مجموع خسائر المفصل للنماذج المصنفة بشكل خاطئ، كما يقيسها hinge_loss function. بشكل افتراضي، يتم تطبيق التنظيم مع المعلمة C=1، مما يسمح بدرجة معينة من تسامح التصنيف الخاطئ.
إذا لم تكن البيانات قابلة للفصل الخطي في مساحة الميزة الأصلية، يمكن تعيين معلمة النواة غير الخطية. اعتمادًا على النواة، تتضمن العملية إضافة ميزات جديدة أو تحويل الميزات الموجودة لإثراء البيانات وإضافة معنى محتمل لها.
عندما يتم تعيين نواة أخرى غير "linear"، تطبق SVC خدعة النواة kernel trick، والتي تحسب التشابه بين أزواج نقاط البيانات باستخدام دالة النواة دون تحويل مجموعة البيانات بالكامل بشكل صريح. تتجاوز خدعة النواة تحويل المصفوفة الضروري لمجموعة البيانات بالكامل من خلال النظر فقط في العلاقات بين جميع أزواج نقاط البيانات. تقوم دالة النواة بتخطيط متجهين (كل زوج من الملاحظات) إلى تشابههما باستخدام ناتج الضرب النقطي لهما.
بعد ذلك، يمكن حساب المستوى الفاصل باستخدام دالة النواة كما لو كانت مجموعة البيانات ممثلة في مساحة ذات أبعاد أعلى. يؤدي استخدام دالة النواة بدلاً من تحويل مصفوفة صريحة إلى تحسين الأداء، حيث أن دالة النواة لها تعقيد زمني من \(O({n}^2)\)، في حين أن تحويل المصفوفة يتدرج وفقًا لتحويل محدد يجري تطبيقه.
في هذا المثال، نقارن بين أكثر أنواع النواة شيوعًا لآلات المتجهات الداعمة: النواة الخطية ("linear")، ونواة متعددة الحدود ("poly")، ونواة دالة الأساس الشعاعي ("rbf") ونواة سيجمويد ("sigmoid").
# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause
إنشاء مجموعة بيانات#
نحن ننشئ مجموعة بيانات تصنيف ثنائية الأبعاد مع 16 عينة وفئتين. نحن نرسم العينات مع الألوان المطابقة لأهدافها.
import matplotlib.pyplot as plt
import numpy as np
X = np.array(
[
[0.4, -0.7],
[-1.5, -1.0],
[-1.4, -0.9],
[-1.3, -1.2],
[-1.1, -0.2],
[-1.2, -0.4],
[-0.5, 1.2],
[-1.5, 2.1],
[1.0, 1.0],
[1.3, 0.8],
[1.2, 0.5],
[0.2, -2.0],
[0.5, -2.4],
[0.2, -2.3],
[0.0, -2.7],
[1.3, 2.1],
]
)
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])
# إعدادات الرسم
fig, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# رسم العينات حسب اللون وإضافة الأسطورة
scatter = ax.scatter(X[:, 0], X[:, 1], s=150, c=y, label=y, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
ax.set_title("Samples in two-dimensional feature space")
_ = plt.show()
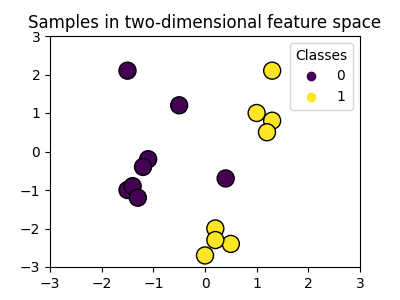
يمكننا أن نرى أن العينات ليست قابلة للفصل بوضوح بخط مستقيم.
تدريب نموذج SVC ورسم حدود القرار#
نحن نحدد دالة تناسب SVC classifier،
السماح بمعلمة kernel كإدخال، ثم رسم حدود القرار
تعلمها بواسطة النموذج باستخدام
DecisionBoundaryDisplay.
لاحظ أنه من أجل التبسيط، يتم تعيين معلمة C إلى قيمتها الافتراضية (C=1) في هذا المثال، ويتم تعيين معلمة gamma إلى
gamma=2 عبر جميع النوى، على الرغم من أنه يتم تجاهلها تلقائيًا للنواة الخطية. في مهمة تصنيف حقيقية، حيث يهم الأداء،
يوصى بضبط المعلمات (باستخدام GridSearchCV على
سبيل المثال) لتحسين أداء النموذج.
تعيين response_method="predict" في
DecisionBoundaryDisplay يلون المناطق بناءً على
فئتها المتوقعة. باستخدام response_method="decision_function" يسمح لنا
أيضًا برسم حدود القرار والهوامش على جانبيه.
وأخيرًا، يتم تحديد المتجهات الداعمة المستخدمة أثناء التدريب (التي تتواجد دائمًا على الهوامش)
من خلال سمة support_vectors_ للناقل الداعم المدرب، ويتم رسمها أيضًا.
from sklearn import svm
from sklearn.inspection import DecisionBoundaryDisplay
def plot_training_data_with_decision_boundary(
kernel, ax=None, long_title=True, support_vectors=True
):
# تدريب SVC
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, y)
# إعدادات الرسم
if ax is None:
_, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))
# رسم حدود القرار والهوامش
common_params = {"estimator": clf, "X": X, "ax": ax}
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="predict",
plot_method="pcolormesh",
alpha=0.3,
)
DecisionBoundaryDisplay.from_estimator(
**common_params,
response_method="decision_function",
plot_method="contour",
levels=[-1, 0, 1],
colors=["k", "k", "k"],
linestyles=["--", "-", "--"],
)
if support_vectors:
# رسم دوائر أكبر حول العينات التي تعمل كمتجهات داعمة
ax.scatter(
clf.support_vectors_[:, 0],
clf.support_vectors_[:, 1],
s=150,
facecolors="none",
edgecolors="k",
)
# رسم العينات حسب اللون وإضافة الأسطورة
ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
if long_title:
ax.set_title(f" Decision boundaries of {kernel} kernel in SVC")
else:
ax.set_title(kernel)
if ax is None:
plt.show()
النواة الخطية#
النواة الخطية هي ناتج الضرب النقطي لعينات الإدخال:
يتم تطبيقها بعد ذلك على أي مجموعة من نقطتي بيانات (عينات) في
مجموعة البيانات. ناتج الضرب النقطي للنقاطتين يحدد
cosine_similarity بين كلتا النقطتين. كلما كانت القيمة أعلى، كلما كانت النقاط أكثر تشابهًا.
plot_training_data_with_decision_boundary("linear")
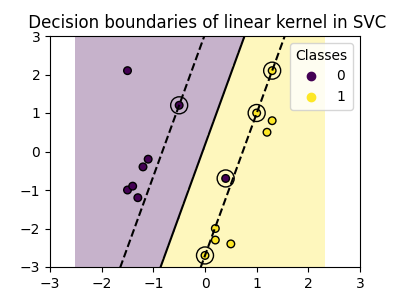
يؤدي تدريب SVC على نواة خطية إلى مساحة ميزات غير محولة، حيث يكون المستوى الفاصل والهوامش
خطوط مستقيمة. بسبب نقص التعبير عن النواة الخطية، لا تلتقط الفئات المدربة بيانات التدريب بشكل مثالي.
النواة متعددة الحدود#
تغير النواة متعددة الحدود مفهوم التشابه. يتم تعريف دالة النواة على النحو التالي:
حيث \({d}\) هي الدرجة (degree) للمتعددة الحدود، \({\gamma}\)
(gamma) يتحكم في تأثير كل عينة تدريب فردية على
حدود القرار و \({r}\) هو مصطلح التحيز (coef0) الذي يتحرك البيانات لأعلى أو لأسفل. هنا، نستخدم القيمة الافتراضية لدرجة متعددة الحدود
في دالة النواة (degree=3). عندما coef0=0 (الافتراضي)،
يتم تحويل البيانات فقط، ولكن لا يتم إضافة بعد إضافي. استخدام
نواة متعددة الحدود يعادل إنشاء
PolynomialFeatures ثم تناسب
SVC مع نواة خطية على البيانات المحولة،
على الرغم من أن هذا النهج البديل سيكون مكلفًا من الناحية الحسابية لمعظم
مجموعات البيانات.
plot_training_data_with_decision_boundary("poly")
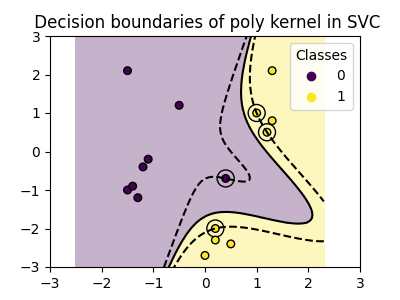
تتكيف النواة متعددة الحدود مع gamma=2 بشكل جيد مع بيانات التدريب،
مما يتسبب في انحناء الهوامش على جانبي المستوى الفاصل وفقًا لذلك.
نواة دالة الأساس الشعاعي#
نواة دالة الأساس الشعاعي (RBF)، والمعروفة أيضًا as النواة الغاوسية، هي النواة الافتراضية لآلات المتجهات الداعمة في scikit-learn. تقيس التشابه بين نقطتي بيانات في أبعاد لانهائية ثم تقترب من التصنيف بالتصويت بالأغلبية. يتم تعريف دالة النواة على النحو التالي:
حيث \({\gamma}\) (gamma) يتحكم في تأثير كل
عينة تدريب فردية على حدود القرار.
كلما كانت المسافة الإقليدية بين نقطتين أكبر \(\|\mathbf{x}_1 - \mathbf{x}_2\|^2\) كلما كانت دالة النواة أقرب إلى الصفر. هذا يعني أن النقطتين البعيدتين من المرجح أن تكونا غير متشابهتين.
plot_training_data_with_decision_boundary("rbf")
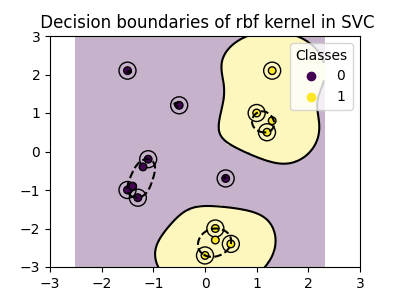
في الرسم البياني، يمكننا أن نرى كيف تميل حدود القرار إلى الانكماش حول نقاط البيانات القريبة من بعضها البعض.
نواة سيجمويد#
يتم تعريف دالة نواة سيجمويد على النحو التالي:
حيث معامل النواة \({\gamma}\) (gamma) يتحكم في التأثير
من كل عينة تدريب فردية على حدود القرار و \({r}\) هو
مصطلح التحيز (coef0) الذي يتحرك البيانات لأعلى أو لأسفل.
في نواة سيجمويد، يتم حساب التشابه بين نقطتي بيانات باستخدام دالة التانجنت فرطية (\(\tanh\)). تقوم دالة النواة بتوسيع نطاق ناتج الضرب النقطي للنقاطتين (\(\mathbf{x}_1\) و \(\mathbf{x}_2\)).
plot_training_data_with_decision_boundary("sigmoid")
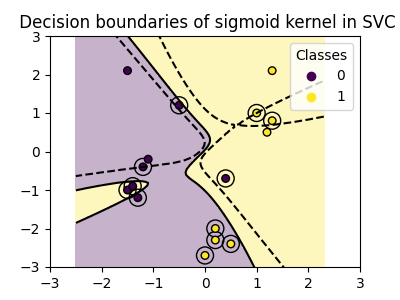
يمكننا أن نرى أن حدود القرار التي تم الحصول عليها مع نواة سيجمويد تظهر منحنية وغير منتظمة. تحاول حدود القرار فصل الفئات عن طريق تناسب منحنى على شكل سيجمويد، مما يؤدي إلى حدود معقدة قد لا تعمم جيدًا على البيانات غير المرئية. من هذا المثال يصبح واضحًا، أن نواة سيجمويد لها حالات استخدام محددة جدًا، عند التعامل مع البيانات التي تعرض شكل سيجمويد. في هذا المثال، قد يجد الضبط الدقيق حدودًا أكثر عمومية. بسبب خصوصيتها، يتم استخدام نواة سيجمويد بشكل أقل شيوعًا في الممارسة العملية مقارنةً بالنوى الأخرى.
الخلاصة#
في هذا المثال، قمنا بتصور حدود القرار المدربة باستخدام مجموعة البيانات المقدمة. تخدم الرسوم البيانية كعرض توضيحي بديهي لكيفية استخدام النوى المختلفة لبيانات التدريب لتحديد حدود التصنيف.
يمكن تخيل المستويات الفاصلة والهوامش، على الرغم من حسابها بشكل غير مباشر، كمساحات في مساحة الميزة المحولة. ومع ذلك، في الرسوم البيانية، يتم تمثيلها بالنسبة لمساحة الميزة الأصلية، مما يؤدي إلى حدود قرار منحنية للنواة متعددة الحدود، وRBF، ونواة سيجمويد.
يرجى ملاحظة أن الرسوم البيانية لا تقيم دقة النواة الفردية أو جودتها. القصد منها هو توفير فهم مرئي لكيفية استخدام النوى المختلفة لبيانات التدريب.
من أجل التقييم الشامل، يوصى بضبط معلمات SVC
باستخدام تقنيات مثل
GridSearchCV لالتقاط الهياكل الأساسية داخل
البيانات.
مجموعة بيانات XOR#
مثال كلاسيكي لمجموعة بيانات غير قابلة للفصل الخطي هو نمط XOR. هنا نبين كيف تعمل النوى المختلفة على مثل هذه مجموعة البيانات.
xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
_, ax = plt.subplots(2, 2, figsize=(8, 8))
args = dict(long_title=False, support_vectors=False)
plot_training_data_with_decision_boundary("linear", ax[0, 0], **args)
plot_training_data_with_decision_boundary("poly", ax[0, 1], **args)
plot_training_data_with_decision_boundary("rbf", ax[1, 0], **args)
plot_training_data_with_decision_boundary("sigmoid", ax[1, 1], **args)
plt.show()
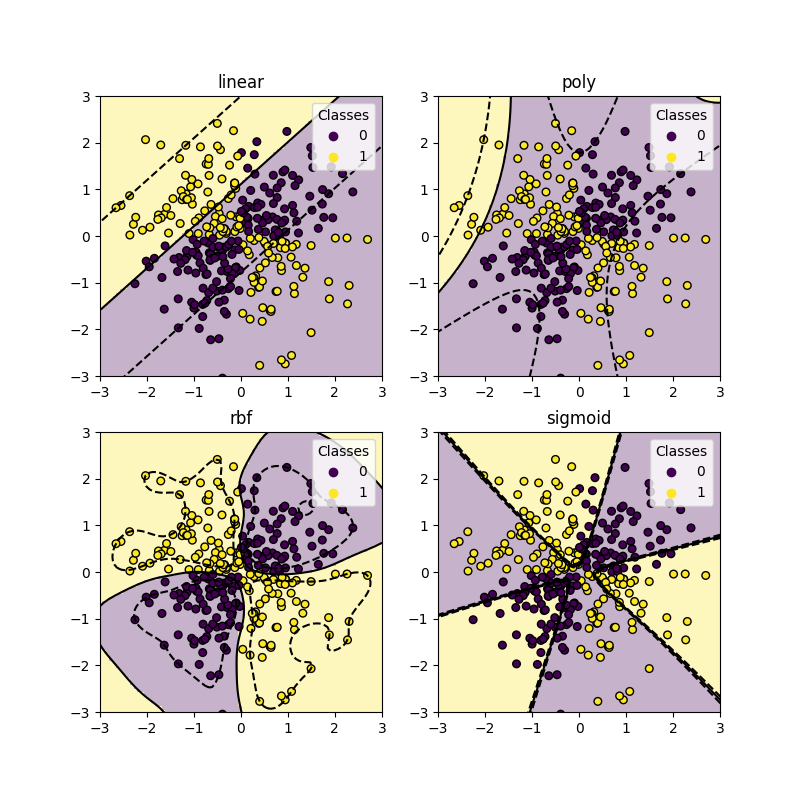
كما يمكنك أن ترى من الرسوم البيانية أعلاه، فقط نواة rbf يمكنها إيجاد
حدود قرار معقولة لمجموعة البيانات أعلاه.
Total running time of the script: (0 minutes 1.513 seconds)
Related examples
رسم مخططات لمصنفات SVM المختلفة في مجموعة بيانات الزهرة
مقارنة انحدار kernel ridge وانحدار العمليات الغاوسية