ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
مخططات التبعية الجزئية والتوقع الشرطي الفردي#
توضح مخططات التبعية الجزئية العلاقة بين دالة الهدف [2] ومجموعة من الميزات محل الاهتمام، مع تهميش قيم جميع الميزات الأخرى (الميزات المتممة). نظرًا لحدود الإدراك البشري، يجب أن يكون حجم مجموعة الميزات محل الاهتمام صغيرًا (عادةً، واحد أو اثنين) وبالتالي يتم اختيارها عادةً من بين أهم الميزات.
وبالمثل، يُظهر مخطط التوقع الشرطي الفردي (ICE) [3] العلاقة بين دالة الهدف وميزة محل الاهتمام. ومع ذلك، على عكس مخططات التبعية الجزئية، والتي تُظهر متوسط تأثير الميزات محل الاهتمام، تُظهر مخططات ICE التبعية بين التنبؤ وميزة لكل عينة على حدة، مع سطر واحد لكل عينة. يتم دعم ميزة واحدة فقط محل الاهتمام لمخططات ICE.
يوضح هذا المثال كيفية الحصول على مخططات التبعية الجزئية و ICE من
MLPRegressor و
HistGradientBoostingRegressor مُدرَّب على مجموعة بيانات مشاركة الدراجات. المثال مستوحى من [1].
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
معالجة مسبقة لمجموعة بيانات مشاركة الدراجات#
سنستخدم مجموعة بيانات مشاركة الدراجات. الهدف هو التنبؤ بعدد تأجيرات الدراجات باستخدام بيانات الطقس والموسم بالإضافة إلى معلومات التاريخ والوقت.
from sklearn.datasets import fetch_openml
bikes = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
# إنشاء نسخة صريحة لتجنب "SettingWithCopyWarning" من pandas
X, y = bikes.data.copy(), bikes.target
# نستخدم فقط مجموعة فرعية من البيانات لتسريع المثال.
X = X.iloc[::5, :]
y = y[::5]
تتميز الميزة "weather" بخصوصية: الفئة "heavy_rain" فئة نادرة.
X["weather"].value_counts()
weather
clear 2284
misty 904
rain 287
heavy_rain 1
Name: count, dtype: int64
بسبب هذه الفئة النادرة، نقوم بدمجها في "rain".
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
نلقي نظرة فاحصة الآن على الميزة "year":
X["year"].value_counts()
year
1 1747
0 1729
Name: count, dtype: int64
نرى أن لدينا بيانات من عامين. نستخدم السنة الأولى لتدريب النموذج والسنة الثانية لاختبار النموذج.
mask_training = X["year"] == 0.0
X = X.drop(columns=["year"])
X_train, y_train = X[mask_training], y[mask_training]
X_test, y_test = X[~mask_training], y[~mask_training]
يمكننا التحقق من معلومات مجموعة البيانات لمعرفة أن لدينا أنواع بيانات غير متجانسة. علينا معالجة الأعمدة المختلفة مسبقًا وفقًا لذلك.
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 1729 entries, 0 to 8640
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 1729 non-null category
1 month 1729 non-null int64
2 hour 1729 non-null int64
3 holiday 1729 non-null category
4 weekday 1729 non-null int64
5 workingday 1729 non-null category
6 weather 1729 non-null category
7 temp 1729 non-null float64
8 feel_temp 1729 non-null float64
9 humidity 1729 non-null float64
10 windspeed 1729 non-null float64
dtypes: category(4), float64(4), int64(3)
memory usage: 115.4 KB
من المعلومات السابقة، سنعتبر أعمدة category كميزات فئوية اسمية. بالإضافة إلى ذلك، سنعتبر معلومات التاريخ والوقت كميزات فئوية أيضًا.
نقوم بتعريف الأعمدة التي تحتوي على ميزات رقمية وفئوية يدويًا.
numerical_features = [
"temp",
"feel_temp",
"humidity",
"windspeed",
]
categorical_features = X_train.columns.drop(numerical_features)
قبل الخوض في التفاصيل المتعلقة بالمعالجة المسبقة لخطوط أنابيب التعلم الآلي المختلفة، سنحاول الحصول على بعض الأفكار الإضافية بخصوص مجموعة البيانات التي ستكون مفيدة لفهم الأداء الإحصائي للنموذج ونتائج تحليل التبعية الجزئية.
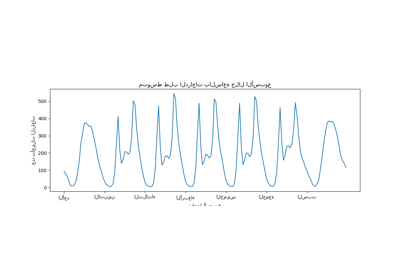
نرسم متوسط عدد تأجيرات الدراجات عن طريق تجميع البيانات حسب الموسم وحسب السنة.
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
days = ("Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat")
hours = tuple(range(24))
xticklabels = [f"{day}\n{hour}:00" for day, hour in product(days, hours)]
xtick_start, xtick_period = 6, 12
fig, axs = plt.subplots(nrows=2, figsize=(8, 6), sharey=True, sharex=True)
average_bike_rentals = bikes.frame.groupby(
["year", "season", "weekday", "hour"], observed=True
).mean(numeric_only=True)["count"]
for ax, (idx, df) in zip(axs, average_bike_rentals.groupby("year")):
df.groupby("season", observed=True).plot(ax=ax, legend=True)
# تزيين الرسم
ax.set_xticks(
np.linspace(
start=xtick_start,
stop=len(xticklabels),
num=len(xticklabels) // xtick_period,
)
)
ax.set_xticklabels(xticklabels[xtick_start::xtick_period])
ax.set_xlabel("")
ax.set_ylabel("متوسط عدد تأجيرات الدراجات")
ax.set_title(
f"تأجير الدراجات لـ {'2010 (مجموعة التدريب)' if idx == 0.0 else '2011 (مجموعة الاختبار)'}"
)
ax.set_ylim(0, 1_000)
ax.set_xlim(0, len(xticklabels))
ax.legend(loc=2)
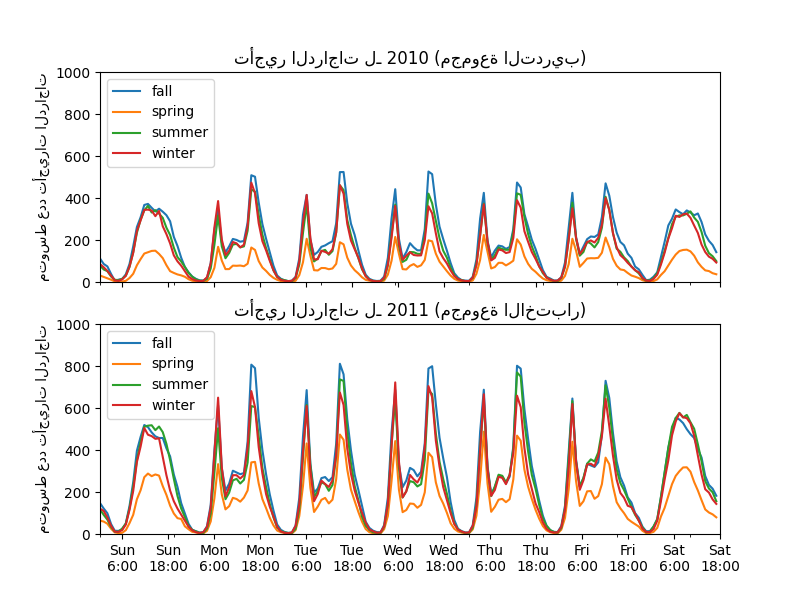
أوضح فرق بين مجموعة التدريب ومجموعة الاختبار هو أن عدد تأجيرات الدراجات أعلى في مجموعة الاختبار. لهذا السبب، لن يكون من المفاجئ الحصول على نموذج تعلم آلي يقلل من شأن عدد تأجيرات الدراجات. نلاحظ أيضًا أن عدد تأجيرات الدراجات أقل خلال فصل الربيع. بالإضافة إلى ذلك، نرى أنه خلال أيام العمل، هناك نمط محدد حوالي الساعة 6-7 صباحًا و 5-6 مساءً مع بعض ذروات تأجيرات الدراجات. يمكننا أن نضع في اعتبارنا هذه الأفكار المختلفة ونستخدمها لفهم مخطط التبعية الجزئية.
المعالج المسبق لنماذج التعلم الآلي#
نظرًا لأننا سنستخدم لاحقًا نموذجين مختلفين،
MLPRegressor و
HistGradientBoostingRegressor، فإننا ننشئ معالجين مسبقين مختلفين، خاصين بكل نموذج.
المعالج المسبق لنموذج الشبكة العصبية#
سنستخدم QuantileTransformer لقياس
الميزات الرقمية وتشفير الميزات الفئوية باستخدام
OneHotEncoder.
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, QuantileTransformer
mlp_preprocessor = ColumnTransformer(
transformers=[
("num", QuantileTransformer(n_quantiles=100), numerical_features),
("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features),
]
)
mlp_preprocessor
المعالج المسبق لنموذج التعزيز التدريجي#
بالنسبة لنموذج التعزيز التدريجي، نترك الميزات الرقمية كما هي ونقوم فقط
بتشفير الميزات الفئوية باستخدام
OrdinalEncoder.
from sklearn.preprocessing import OrdinalEncoder
hgbdt_preprocessor = ColumnTransformer(
transformers=[
("cat", OrdinalEncoder(), categorical_features),
("num", "passthrough", numerical_features),
],
sparse_threshold=1,
verbose_feature_names_out=False,
).set_output(transform="pandas")
hgbdt_preprocessor
التبعية الجزئية أحادية الاتجاه مع نماذج مختلفة#
في هذا القسم، سنحسب التبعية الجزئية أحادية الاتجاه مع نموذجين مختلفين للتعلم الآلي: (1) شبكة عصبية متعددة الطبقات و (2) نموذج تعزيز تدريجي. باستخدام هذين النموذجين، نوضح كيفية حساب وتفسير كل من مخطط التبعية الجزئية (PDP) لكل من الميزات الرقمية والفئوية والتوقع الشرطي الفردي (ICE).
شبكة عصبية متعددة الطبقات#
دعونا نلائم MLPRegressor ونحسب
مخططات التبعية الجزئية أحادية المتغير.
from time import time
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
print("تدريب MLPRegressor...")
tic = time()
mlp_model = make_pipeline(
mlp_preprocessor,
MLPRegressor(
hidden_layer_sizes=(30, 15),
learning_rate_init=0.01,
early_stopping=True,
random_state=0,
),
)
mlp_model.fit(X_train, y_train)
print(f"تم في {time() - tic:.3f} ثانية")
print(f"درجة R2 للاختبار: {mlp_model.score(X_test, y_test):.2f}")
تدريب MLPRegressor...
تم في 0.709 ثانية
درجة R2 للاختبار: 0.61
قمنا بتهيئة خط أنابيب باستخدام المعالج المسبق الذي أنشأناه خصيصًا للشبكة العصبية وقمنا بضبط حجم الشبكة العصبية ومعدل التعلم للحصول على حل وسط معقول بين وقت التدريب والأداء التنبؤي على مجموعة الاختبار.
من المهم أن نلاحظ أن مجموعة البيانات الجدولية هذه لها نطاقات ديناميكية مختلفة جدًا لميزاتها. تميل الشبكات العصبية إلى أن تكون حساسة للغاية للميزات ذات المقاييس المتفاوتة، ونسيان المعالجة المسبقة للميزة الرقمية سيؤدي إلى نموذج ضعيف للغاية.
سيكون من الممكن الحصول على أداء تنبؤي أعلى مع شبكة عصبية أكبر ولكن التدريب سيكون أيضًا أكثر تكلفة بكثير.
لاحظ أنه من المهم التحقق من أن النموذج دقيق بما فيه الكفاية على مجموعة الاختبار قبل رسم التبعية الجزئية حيث سيكون هناك فائدة قليلة في شرح تأثير ميزة معينة على دالة التنبؤ لنموذج ذو أداء تنبؤي ضعيف. في هذا الصدد، يعمل نموذج MLP الخاص بنا بشكل معقول.
سنرسم متوسط التبعية الجزئية.
import matplotlib.pyplot as plt
from sklearn.inspection import PartialDependenceDisplay
common_params = {
"subsample": 50,
"n_jobs": 2,
"grid_resolution": 20,
"random_state": 0,
}
print("حساب مخططات التبعية الجزئية...")
features_info = {
# الميزات محل الاهتمام
"features": ["temp", "humidity", "windspeed", "season", "weather", "hour"],
# نوع مخطط التبعية الجزئية
"kind": "average",
# معلومات بخصوص الميزات الفئوية
"categorical_features": categorical_features,
}
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
mlp_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
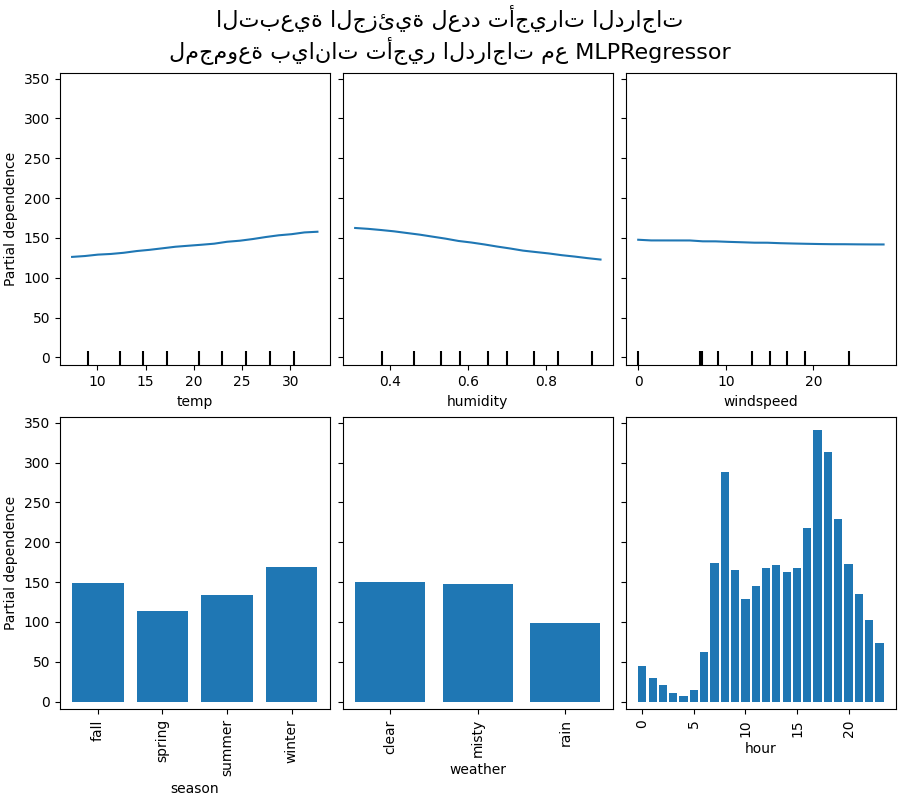
_ = display.figure_.suptitle(
(
"التبعية الجزئية لعدد تأجيرات الدراجات\n"
"لمجموعة بيانات تأجير الدراجات مع MLPRegressor"
),
fontsize=16,
)
حساب مخططات التبعية الجزئية...
تم في 0.714 ثانية
تعزيز تدريجي#
دعونا الآن نلائم HistGradientBoostingRegressor و
نحسب التبعية الجزئية على نفس الميزات. نستخدم أيضًا
المعالج المسبق المحدد الذي أنشأناه لهذا النموذج.
from sklearn.ensemble import HistGradientBoostingRegressor
print("تدريب HistGradientBoostingRegressor...")
tic = time()
hgbdt_model = make_pipeline(
hgbdt_preprocessor,
HistGradientBoostingRegressor(
categorical_features=categorical_features,
random_state=0,
max_iter=50,
),
)
hgbdt_model.fit(X_train, y_train)
print(f"تم في {time() - tic:.3f} ثانية")
print(f"درجة R2 للاختبار: {hgbdt_model.score(X_test, y_test):.2f}")
تدريب HistGradientBoostingRegressor...
تم في 0.166 ثانية
درجة R2 للاختبار: 0.62
هنا، استخدمنا المعلمات الفائقة الافتراضية لنموذج التعزيز التدريجي بدون أي معالجة مسبقة حيث أن النماذج القائمة على الأشجار قوية بشكل طبيعي للتحويلات الرتيبة للميزات الرقمية.
لاحظ أنه في مجموعة البيانات الجدولية هذه، تعد آلات التعزيز التدريجي أسرع بكثير في التدريب وأكثر دقة من الشبكات العصبية. كما أنها أرخص بكثير في ضبط المعلمات الفائقة (تميل الإعدادات الافتراضية إلى العمل بشكل جيد بينما لا يكون هذا هو الحال غالبًا للشبكات العصبية).
سنرسم التبعية الجزئية لبعض الميزات الرقمية والفئوية.
print("حساب مخططات التبعية الجزئية...")
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
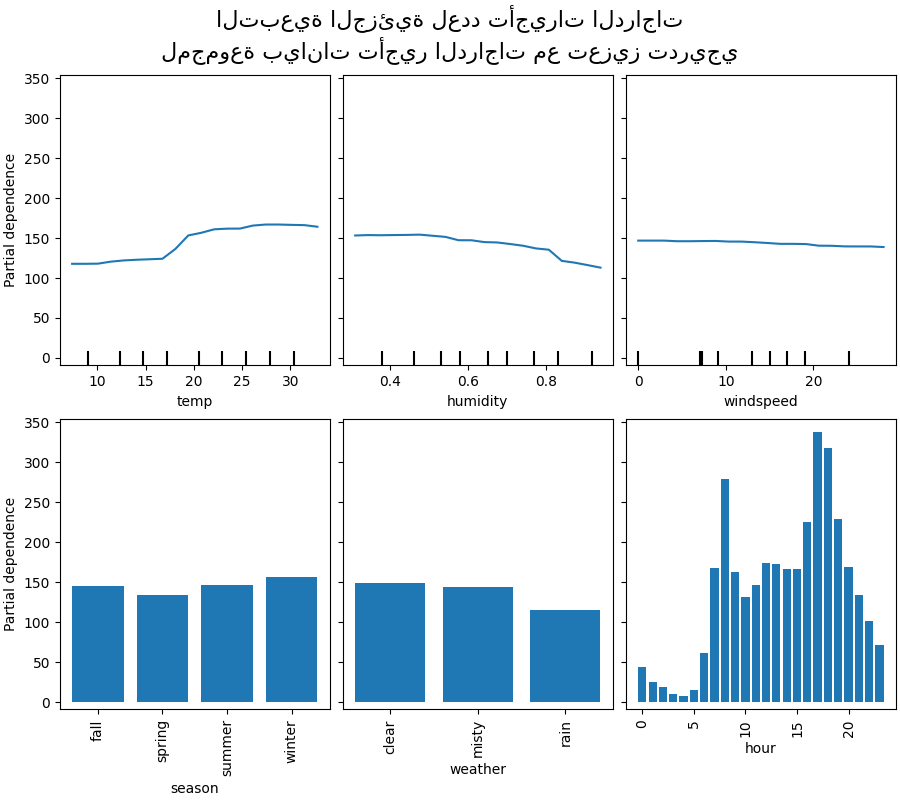
_ = display.figure_.suptitle(
(
"التبعية الجزئية لعدد تأجيرات الدراجات\n"
"لمجموعة بيانات تأجير الدراجات مع تعزيز تدريجي"
),
fontsize=16,
)
حساب مخططات التبعية الجزئية...
تم في 1.522 ثانية
تحليل المخططات#
سننظر أولاً في مخططات PDP للميزات الرقمية. لكلا النموذجين، الاتجاه العام لمخطط PDP لدرجة الحرارة هو أن عدد تأجيرات الدراجات يزداد مع درجة الحرارة. يمكننا إجراء تحليل مشابه ولكن مع اتجاه معاكس لميزات الرطوبة. يتناقص عدد تأجيرات الدراجات عندما تزداد الرطوبة. أخيرًا، نرى نفس الاتجاه لميزة سرعة الرياح. يتناقص عدد تأجيرات الدراجات عندما تزداد سرعة الرياح لكلا النموذجين. نلاحظ أيضًا أن MLPRegressor لديه تنبؤات أكثر سلاسة من HistGradientBoostingRegressor.
الآن، سننظر في مخططات التبعية الجزئية للميزات الفئوية.
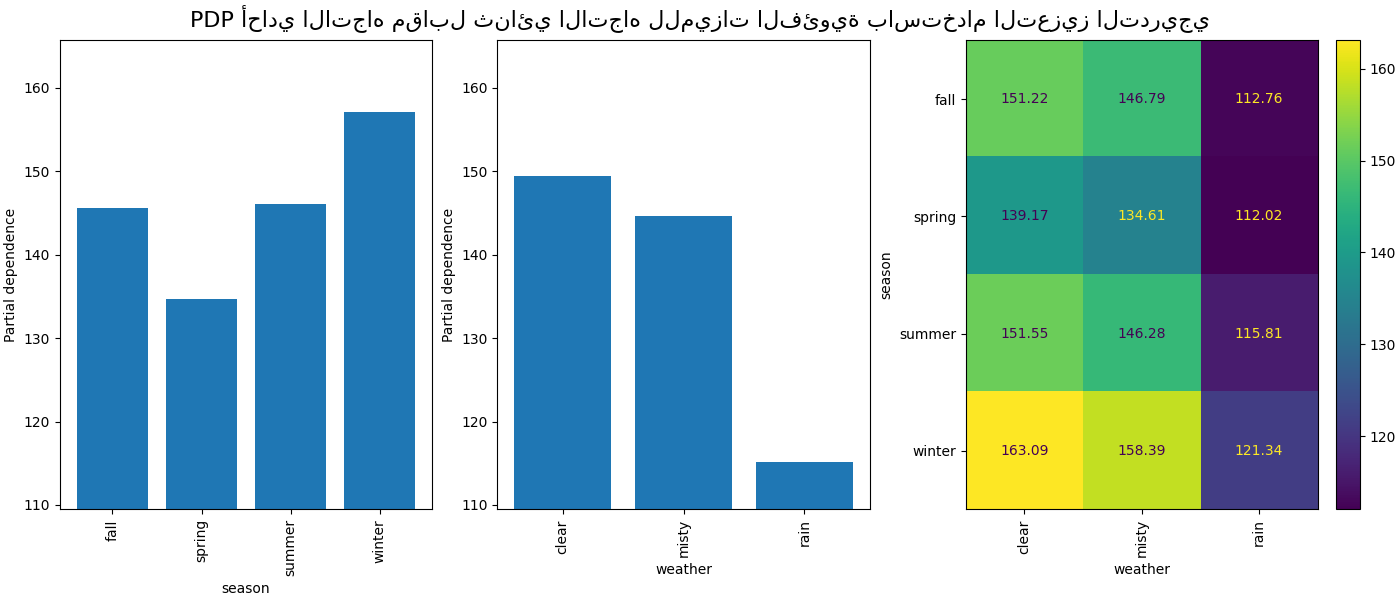
نلاحظ أن فصل الربيع هو أدنى شريط لميزة الموسم. مع ميزة الطقس، تعد فئة المطر هي أدنى شريط. فيما يتعلق بميزة الساعة، نرى ذروتين حوالي الساعة 7 صباحًا و 6 مساءً. تتماشى هذه النتائج مع الملاحظات التي أدلينا بها سابقًا على مجموعة البيانات.
ومع ذلك، تجدر الإشارة إلى أننا نقوم بإنشاء عينات اصطناعية محتملة لا معنى لها إذا كانت الميزات مترابطة.
ICE مقابل PDP#
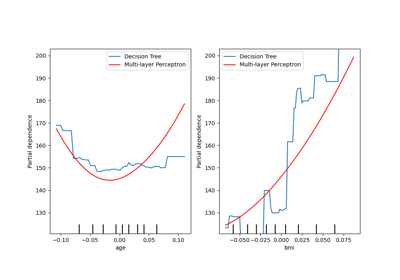
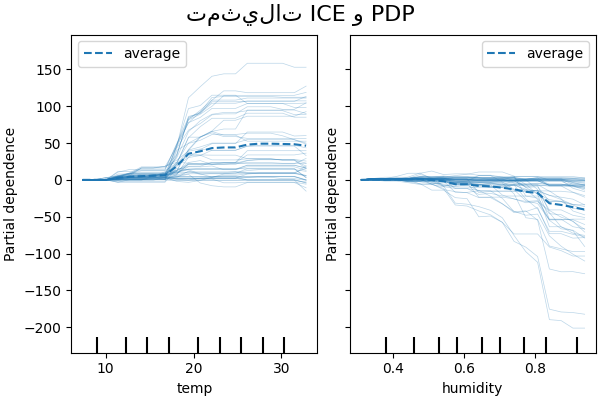
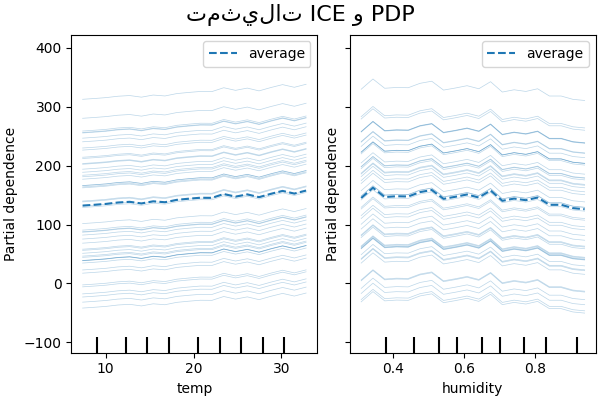
PDP هو متوسط التأثيرات الهامشية للميزات. نحن نحسب متوسط استجابة جميع عينات المجموعة المقدمة. وبالتالي، يمكن إخفاء بعض التأثيرات. في هذا الصدد، من الممكن رسم كل استجابة فردية. يُطلق على هذا التمثيل اسم مخطط التأثير الفردي (ICE). في الرسم التخطيطي أدناه، نرسم 50 ICE تم اختيارها عشوائيًا لميزات درجة الحرارة والرطوبة.
print("حساب مخططات التبعية الجزئية وتوقع الشرطي الفردي...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
"centered": True,
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
_ = display.figure_.suptitle("تمثيلات ICE و PDP", fontsize=16)
حساب مخططات التبعية الجزئية وتوقع الشرطي الفردي...
تم في 0.573 ثانية
نرى أن ICE لميزة درجة الحرارة يمنحنا بعض المعلومات الإضافية: بعض خطوط ICE مسطحة بينما يظهر البعض الآخر انخفاضًا في التبعية لدرجة حرارة أعلى من 35 درجة مئوية. نلاحظ نمطًا مشابهًا لميزة الرطوبة: تظهر بعض خطوط ICE انخفاضًا حادًا عندما تكون الرطوبة أعلى من 80٪.
ليست كل خطوط ICE متوازية، وهذا يشير إلى أن النموذج يجد تفاعلات بين الميزات. يمكننا تكرار التجربة عن طريق تقييد نموذج التعزيز التدريجي على عدم استخدام أي تفاعلات بين الميزات باستخدام المعلمة interaction_cst:
from sklearn.base import clone
interaction_cst = [[i] for i in range(X_train.shape[1])]
hgbdt_model_without_interactions = (
clone(hgbdt_model)
.set_params(histgradientboostingregressor__interaction_cst=interaction_cst)
.fit(X_train, y_train)
)
print(f"درجة R2 للاختبار: {hgbdt_model_without_interactions.score(X_test, y_test):.2f}")
درجة R2 للاختبار: 0.38
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info["centered"] = False
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
_ = display.figure_.suptitle("تمثيلات ICE و PDP", fontsize=16)
مخططات التفاعل ثنائية الأبعاد#
تمكننا مخططات PDP ذات ميزتين محل الاهتمام من تصور التفاعلات بينهما. ومع ذلك، لا يمكن رسم مخططات ICE بطريقة سهلة وبالتالي تفسيرها. سنعرض التمثيل المتاح في
from_estimator وهو عبارة عن خريطة حرارية ثنائية الأبعاد.
print("حساب مخططات التبعية الجزئية...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
_ = display.figure_.suptitle(
"PDP أحادي الاتجاه مقابل ثنائي الاتجاه للمتغيرات الرقمية باستخدام التعزيز التدريجي", fontsize=16
)
حساب مخططات التبعية الجزئية...
تم في 9.920 ثانية
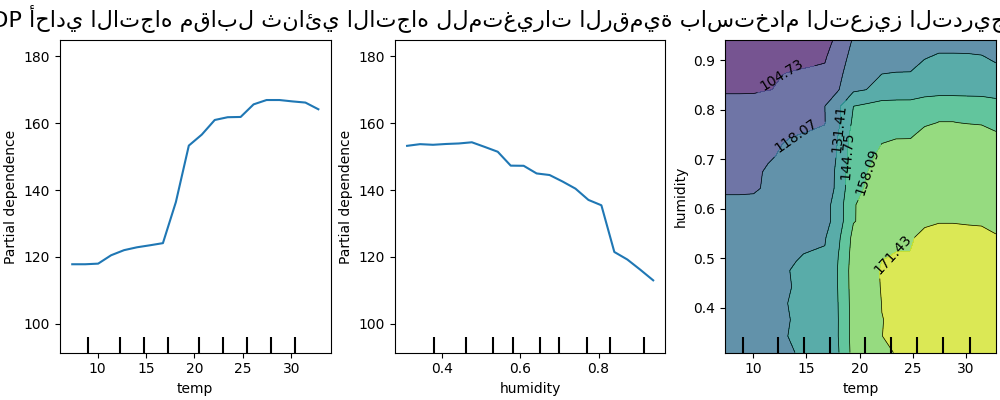
يوضح مخطط التبعية الجزئية ثنائي الاتجاه اعتماد عدد تأجيرات الدراجات على القيم المشتركة لدرجة الحرارة والرطوبة. نرى بوضوح تفاعلًا بين الميزتين. بالنسبة لدرجة حرارة أعلى من 20 درجة مئوية، يكون للرطوبة تأثير على عدد تأجيرات الدراجات يبدو مستقلاً عن درجة الحرارة.
من ناحية أخرى، بالنسبة لدرجات حرارة أقل من 20 درجة مئوية، تؤثر كل من درجة الحرارة والرطوبة بشكل مستمر على عدد تأجيرات الدراجات.
علاوة على ذلك، يعتمد ميل تأثير عتبة 20 درجة مئوية بشدة على مستوى الرطوبة: يكون الانحدار حادًا في ظل الظروف الجافة ولكنه أكثر سلاسة في ظل الظروف الأكثر رطوبة فوق 70٪ من الرطوبة.
نقارن الآن هذه النتائج بنفس المخططات المحسوبة للنموذج المقيد لتعلم دالة تنبؤ لا تعتمد على مثل هذه التفاعلات غير الخطية للميزات.
print("حساب مخططات التبعية الجزئية...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
_ = display.figure_.suptitle(
"PDP أحادي الاتجاه مقابل ثنائي الاتجاه للمتغيرات الرقمية باستخدام التعزيز التدريجي", fontsize=16
)
حساب مخططات التبعية الجزئية...
تم في 8.979 ثانية
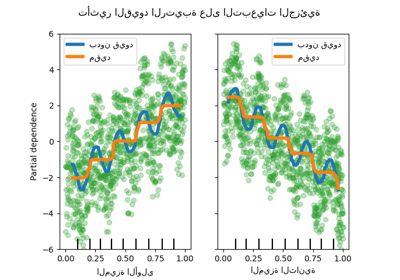
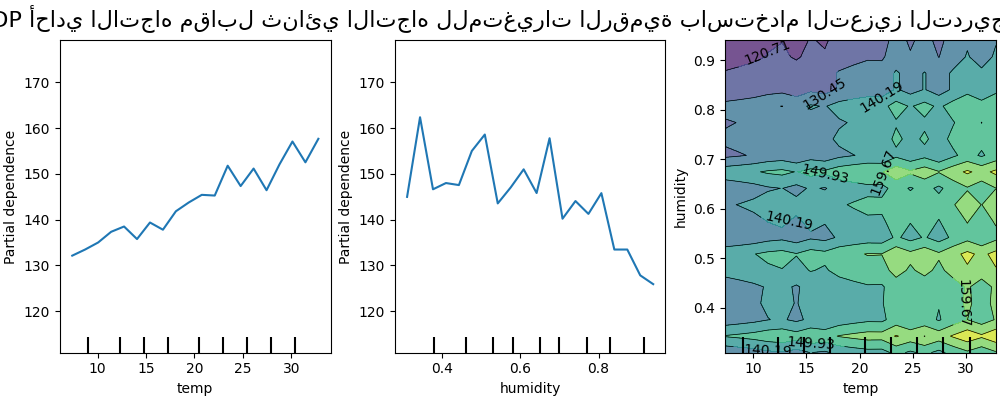
تُظهر مخططات التبعية الجزئية أحادية الأبعاد للنموذج المقيد بعدم نمذجة تفاعلات الميزات ارتفاعات محلية لكل ميزة على حدة، خاصة بالنسبة لميزة "الرطوبة". قد تعكس هذه الارتفاعات سلوكًا متدهورًا للنموذج الذي يحاول بطريقة ما تعويض التفاعلات المحظورة من خلال الإفراط في ملاءمة نقاط تدريب معينة. لاحظ أن الأداء التنبؤي لهذا النموذج كما تم قياسه في مجموعة الاختبار أسوأ بكثير من أداء النموذج الأصلي غير المقيد.
لاحظ أيضًا أن عدد الارتفاعات المحلية المرئية على هذه المخططات يعتمد على معلمة دقة الشبكة لمخطط PD نفسه.
تؤدي هذه الارتفاعات المحلية إلى مخطط PD ثنائي الأبعاد ذو شبكة صاخبة. من الصعب جدًا معرفة ما إذا كان هناك تفاعل بين هذه الميزات أم لا بسبب التذبذبات عالية التردد في ميزة الرطوبة. ومع ذلك، يمكن بوضوح رؤية أن تأثير التفاعل البسيط الذي لوحظ عندما تتجاوز درجة الحرارة حد 20 درجة لم يعد مرئيًا لهذا النموذج.
ستوفر التبعية الجزئية بين الميزات الفئوية تمثيلًا منفصلاً يمكن عرضه كخريطة حرارية. على سبيل المثال، سيكون التفاعل بين الموسم والطقس والهدف كما يلي:
print("حساب مخططات التبعية الجزئية...")
features_info = {
"features": ["season", "weather", ("season", "weather")],
"kind": "average",
"categorical_features": categorical_features,
}
_, ax = plt.subplots(ncols=3, figsize=(14, 6), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"تم في {time() - tic:.3f} ثانية")
_ = display.figure_.suptitle(
"PDP أحادي الاتجاه مقابل ثنائي الاتجاه للميزات الفئوية باستخدام التعزيز التدريجي", fontsize=16
)
حساب مخططات التبعية الجزئية...
تم في 0.447 ثانية
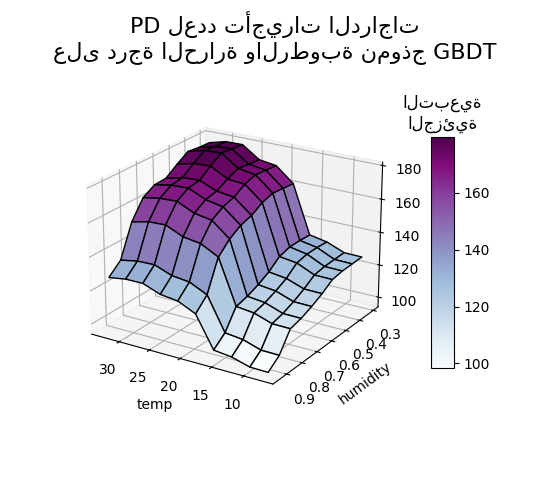
تمثيل ثلاثي الأبعاد#
دعونا ننشئ نفس مخطط التبعية الجزئية لتفاعل الميزتين، هذه المرة بأبعاد ثلاثية. استيراد غير مستخدم ولكنه مطلوب لإجراء إسقاطات ثلاثية الأبعاد مع matplotlib <3.2
import mpl_toolkits.mplot3d # noqa: F401
import numpy as np
from sklearn.inspection import partial_dependence
fig = plt.figure(figsize=(5.5, 5))
features = ("temp", "humidity")
pdp = partial_dependence(
hgbdt_model, X_train, features=features, kind="average", grid_resolution=10
)
XX, YY = np.meshgrid(pdp["grid_values"][0], pdp["grid_values"][1])
Z = pdp.average[0].T
ax = fig.add_subplot(projection="3d")
fig.add_axes(ax)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1, cmap=plt.cm.BuPu, edgecolor="k")
ax.set_xlabel(features[0])
ax.set_ylabel(features[1])
fig.suptitle(
"PD لعدد تأجيرات الدراجات\nعلى درجة الحرارة والرطوبة نموذج GBDT",
fontsize=16,
)
# عرض أولي جميل
ax.view_init(elev=22, azim=122)
clb = plt.colorbar(surf, pad=0.08, shrink=0.6, aspect=10)
clb.ax.set_title("التبعية\nالجزئية")
plt.show()
Total running time of the script: (0 minutes 30.488 seconds)
Related examples