ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

دقة-استدعاء#

مثال على مقياس دقة-استدعاء لتقييم جودة ناتج التصنيف.

دقة-استدعاء هي مقياس مفيد لنجاح التنبؤ عندما تكون الفئات غير متوازنة للغاية. في استرجاع المعلومات، الدقة هي مقياس لجزء العناصر ذات الصلة من العناصر التي تم إرجاعها بالفعل، في حين أن الاستدعاء هو مقياس لجزء العناصر التي تم إرجاعها من بين جميع العناصر التي كان ينبغي إرجاعها. تشير "الصلة" هنا إلى العناصر التي تم تصنيفها بشكل إيجابي، أي الإيجابيات الحقيقية والسلبيات الخاطئة.

الدقة (P) معرفة على أنها عدد الإيجابيات الحقيقية (T_p) على عدد الإيجابيات الحقيقية بالإضافة إلى عدد الإيجابيات الخاطئة (F_p).

\[P = \frac{T_p}{T_p+F_p}\]

الاستدعاء (R) معرف على أنه عدد الإيجابيات الحقيقية (T_p) على عدد الإيجابيات الحقيقية بالإضافة إلى عدد السلبيات الخاطئة (F_n).

\[R = \frac{T_p}{T_p + F_n}\]

يظهر منحنى الدقة-الاستدعاء المقايضة بين الدقة والاستدعاء لعتبات مختلفة. يمثل المساحة العالية تحت المنحنى كلاً من الاستدعاء العالي والدقة العالية. يتم تحقيق الدقة العالية عن طريق وجود عدد قليل من الإيجابيات الخاطئة في النتائج التي تم إرجاعها، ويتم تحقيق الاستدعاء العالي عن طريق وجود عدد قليل من السلبيات الخاطئة في النتائج ذات الصلة. تشير الدرجات العالية لكل من الدقة والاستدعاء إلى أن المصنف يعيد النتائج الدقيقة (دقة عالية)، بالإضافة إلى إعادة غالبية جميع النتائج ذات الصلة (استدعاء عالي).

النظام ذو الاستدعاء العالي ولكن الدقة المنخفضة يعيد معظم العناصر ذات الصلة، ولكن نسبة النتائج التي تم إرجاعها والتي تم تصنيفها بشكل خاطئ مرتفعة. النظام ذو الدقة العالية ولكن الاستدعاء المنخفض هو العكس تماماً، حيث يعيد عددًا قليلًا جدًا من العناصر ذات الصلة، ولكن معظم التصنيفات المتوقعة صحيحة عند مقارنتها بالتصنيفات الفعلية. النظام المثالي ذو الدقة العالية والاستدعاء العالي سيعيد معظم العناصر ذات الصلة، مع تصنيف معظم النتائج بشكل صحيح.

يظهر تعريف الدقة (frac{T_p}{T_p + F_p}) أن خفض عتبة المصنف قد يزيد من البسط، عن طريق زيادة عدد النتائج التي تم إرجاعها. إذا تم تعيين العتبة مسبقًا بشكل مرتفع للغاية، فقد تكون النتائج الجديدة جميعها إيجابيات حقيقية، مما يزيد من الدقة. إذا كانت العتبة السابقة مناسبة أو منخفضة للغاية، فإن خفض العتبة أكثر من ذلك سيعرض الإيجابيات الخاطئة، مما يقلل من الدقة.

الاستدعاء معرف على أنه frac{T_p}{T_p+F_n}، حيث لا يعتمد T_p+F_n على عتبة المصنف. لا يمكن لتغيير عتبة المصنف إلا تغيير البسط، T_p. قد يزيد خفض عتبة المصنف من الاستدعاء، عن طريق زيادة عدد نتائج الإيجابيات الحقيقية. من الممكن أيضًا أن يترك خفض العتبة الاستدعاء دون تغيير، بينما تتقلب الدقة. وبالتالي، فإن الدقة لا تنخفض بالضرورة مع الاستدعاء.

يمكن ملاحظة العلاقة بين الاستدعاء والدقة في منطقة الدرج في الرسم البياني - عند حواف هذه الخطوات، يؤدي التغيير الصغير في العتبة إلى تقليل الدقة بشكل كبير، مع مكسب بسيط في الاستدعاء.

الدقة المتوسطة (AP) تلخص مثل هذا الرسم البياني على أنه المتوسط المرجح للدقة التي تم تحقيقها عند كل عتبة، مع استخدام الزيادة في الاستدعاء من العتبة السابقة كوزن:

\(\text{AP} = \sum_n (R_n - R_{n-1}) P_n\)

حيث P_n وR_n هي الدقة والاستدعاء عند العتبة nth. يشار إلى زوج (R_k, P_k) على أنه نقطة تشغيل.

AP والمساحة المثلثية تحت نقاط التشغيل (sklearn.metrics.auc) هي طرق شائعة لتلخيص منحنى دقة-استدعاء تؤدي إلى نتائج مختلفة. اقرأ المزيد في: دليل المستخدم.

تستخدم منحنيات دقة-استدعاء عادةً في التصنيف الثنائي لدراسة ناتج المصنف. من أجل تمديد منحنى دقة-استدعاء والدقة المتوسطة إلى التصنيف متعدد الفئات أو متعدد التصنيفات، من الضروري جعل الناتج ثنائي القيمة. يمكن رسم منحنى واحد لكل تصنيف، ولكن يمكن أيضًا رسم منحنى دقة-استدعاء عن طريق اعتبار كل عنصر من مصفوفة مؤشر التصنيف على أنه تنبؤ ثنائي القيمة (المتوسط الدقيق).

ملاحظة

راجع أيضًا: sklearn.metrics.average_precision_score، sklearn.metrics.recall_score، sklearn.metrics.precision_score، sklearn.metrics.f1_score

# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause

في إعدادات التصنيف الثنائي#

مجموعة البيانات والنموذج#

سنستخدم مصنف Linear SVC للتمييز بين نوعين من زهرة السوسن.

import numpy as np

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)

# إضافة ميزات عشوائية
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)

# تقييد الفئتين الأوليين، وتقسيمهما إلى تدريب واختبار
X_train, X_test, y_train, y_test = train_test_split(
    X[y < 2], y[y < 2], test_size=0.5, random_state=random_state
)

يتوقع Linear SVC أن يكون لكل ميزة نطاقًا مماثلاً من القيم. لذلك، سنقوم أولاً بضبط البيانات باستخدام StandardScaler.

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

classifier = make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
classifier.fit(X_train, y_train)

Pipeline(steps=[('standardscaler', StandardScaler()),
                ('linearsvc',
                 LinearSVC(random_state=RandomState(MT19937) at 0x7F5D4E1E4C40))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

رسم منحنى دقة-استدعاء#

لرسم منحنى دقة-استدعاء، يجب استخدام PrecisionRecallDisplay. في الواقع، هناك طريقتان متاحتان اعتمادًا على ما إذا كنت قد حسبت تنبؤات المصنف أم لا.

دعنا نرسم أولاً منحنى دقة-استدعاء بدون تنبؤات المصنف. نستخدم from_estimator الذي يحسب التنبؤات لنا قبل رسم المنحنى.

from sklearn.metrics import PrecisionRecallDisplay

display = PrecisionRecallDisplay.from_estimator(
    classifier, X_test, y_test, name="LinearSVC", plot_chance_level=True
)
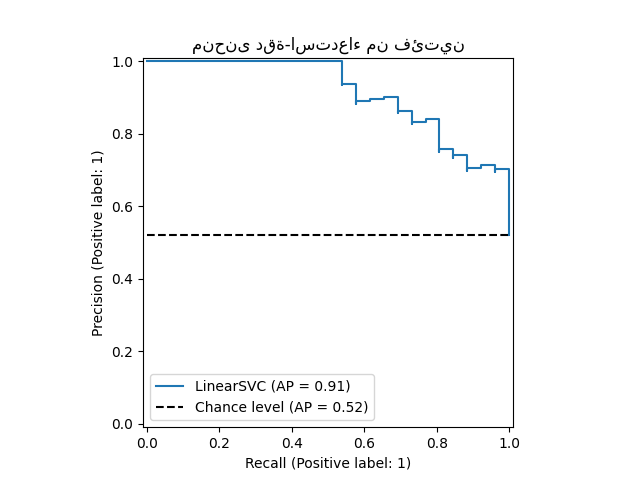
_ = display.ax_.set_title("منحنى دقة-استدعاء من فئتين")

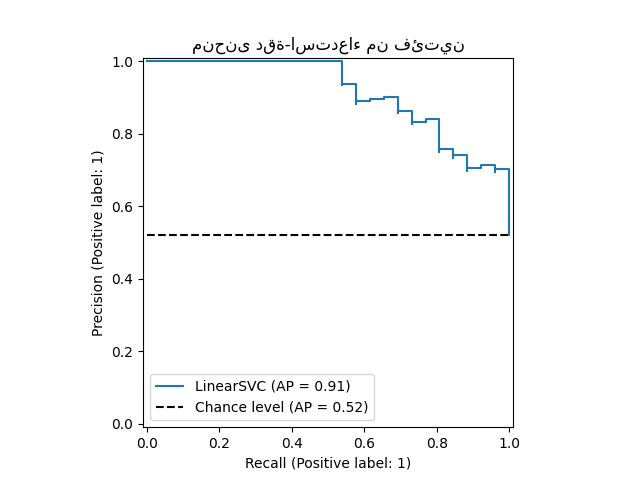
إذا حصلنا بالفعل على الاحتمالات أو الدرجات المقدرة لنموذجنا، فيمكننا استخدام from_predictions.

y_score = classifier.decision_function(X_test)

display = PrecisionRecallDisplay.from_predictions(
    y_test, y_score, name="LinearSVC", plot_chance_level=True
)
_ = display.ax_.set_title("منحنى دقة-استدعاء من فئتين")

في إعدادات متعددة التصنيفات#

لا يدعم منحنى دقة-استدعاء إعداد التصنيف متعدد التصنيفات. ومع ذلك، يمكن للمرء أن يقرر كيفية التعامل مع هذه الحالة. نعرض مثل هذا المثال أدناه.

إنشاء بيانات متعددة التصنيفات، والتدريب، والتنبؤ#

ننشئ مجموعة بيانات متعددة التصنيفات، لتوضيح دقة-استدعاء في إعدادات متعددة التصنيفات.

from sklearn.preprocessing import label_binarize

# استخدام label_binarize ليكون مثل إعدادات متعددة التصنيفات
Y = label_binarize(y, classes=[0, 1, 2])
n_classes = Y.shape[1]

# تقسيمها إلى تدريب واختبار
X_train, X_test, Y_train, Y_test = train_test_split(
    X, Y, test_size=0.5, random_state=random_state
)

نستخدم OneVsRestClassifier للتنبؤ متعدد التصنيفات.

from sklearn.multiclass import OneVsRestClassifier

classifier = OneVsRestClassifier(
    make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
)
classifier.fit(X_train, Y_train)
y_score = classifier.decision_function(X_test)

متوسط درجة الدقة في إعدادات متعددة التصنيفات#

from sklearn.metrics import average_precision_score, precision_recall_curve

# لكل فئة
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
    precision[i], recall[i], _ = precision_recall_curve(Y_test[:, i], y_score[:, i])
    average_precision[i] = average_precision_score(Y_test[:, i], y_score[:, i])

# "متوسط دقيق": تحديد درجة على جميع الفئات بشكل مشترك
precision["micro"], recall["micro"], _ = precision_recall_curve(
    Y_test.ravel(), y_score.ravel()
)
average_precision["micro"] = average_precision_score(Y_test, y_score, average="micro")

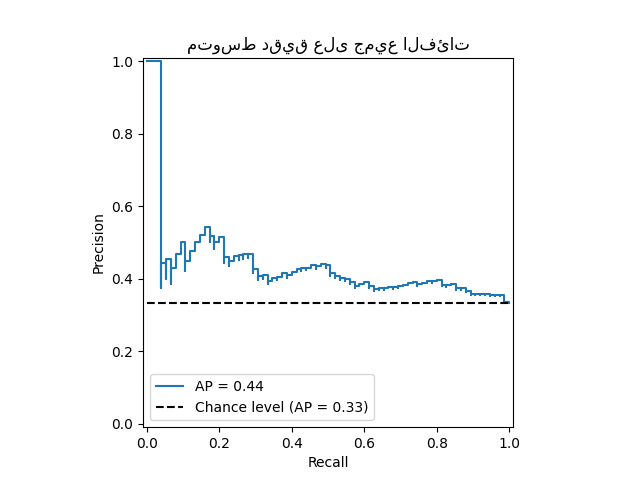
رسم منحنى دقة-استدعاء متوسط دقيق#

from collections import Counter

display = PrecisionRecallDisplay(
    recall=recall["micro"],
    precision=precision["micro"],
    average_precision=average_precision["micro"],
    prevalence_pos_label=Counter(Y_test.ravel())[1] / Y_test.size,
)
display.plot(plot_chance_level=True)
_ = display.ax_.set_title("متوسط دقيق على جميع الفئات")

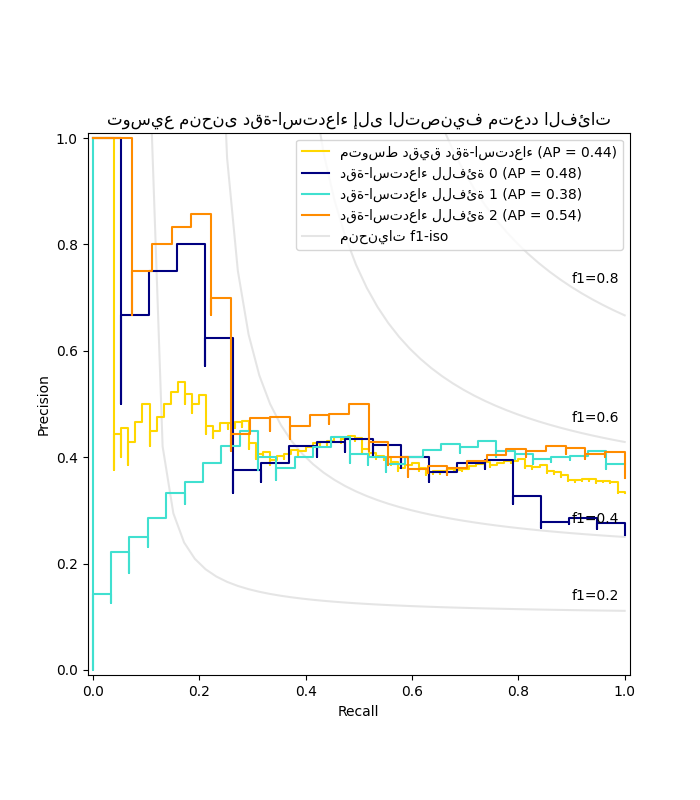
رسم منحنى دقة-استدعاء لكل فئة ومنحنيات f1-iso#

from itertools import cycle

import matplotlib.pyplot as plt

# إعداد تفاصيل الرسم
colors = cycle(["navy", "turquoise", "darkorange", "cornflowerblue", "teal"])

_, ax = plt.subplots(figsize=(7, 8))

f_scores = np.linspace(0.2, 0.8, num=4)
lines, labels = [], []
for f_score in f_scores:
    x = np.linspace(0.01, 1)
    y = f_score * x / (2 * x - f_score)
    (l,) = plt.plot(x[y >= 0], y[y >= 0], color="gray", alpha=0.2)
    plt.annotate("f1={0:0.1f}".format(f_score), xy=(0.9, y[45] + 0.02))

display = PrecisionRecallDisplay(
    recall=recall["micro"],
    precision=precision["micro"],
    average_precision=average_precision["micro"],
)
display.plot(ax=ax, name="متوسط دقيق دقة-استدعاء", color="gold")

for i, color in zip(range(n_classes), colors):
    display = PrecisionRecallDisplay(
        recall=recall[i],
        precision=precision[i],
        average_precision=average_precision[i],
    )
    display.plot(
        ax=ax, name=f"دقة-استدعاء للفئة {i}", color=color
    )

# إضافة الأسطورة لمنحنيات f1-iso
handles, labels = display.ax_.get_legend_handles_labels()
handles.extend([l])
labels.extend(["منحنيات f1-iso"])
# تعيين الأسطورة والمحاور
ax.legend(handles=handles, labels=labels, loc="best")
ax.set_title("توسيع منحنى دقة-استدعاء إلى التصنيف متعدد الفئات")

plt.show()