ملاحظة
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
الميزات المتأخرة للتنبؤ بالسلاسل الزمنية#
هذا المثال يوضح كيفية استخدام الميزات المتأخرة التي تم تصميمها بواسطة Polars في التنبؤ بالسلاسل الزمنية باستخدام HistGradientBoostingRegressor على مجموعة بيانات طلب مشاركة الدراجات.
راجع المثال على هندسة الميزات ذات الصلة بالوقت لاستكشاف بعض البيانات حول هذه المجموعة والاطلاع على عرض توضيحي حول الهندسة الميزات الدورية.
# المؤلفون: مطوري scikit-learn
# معرف SPDX-License: BSD-3-Clause
تحليل مجموعة بيانات طلب مشاركة الدراجات#
نبدأ بتحميل البيانات من مستودع OpenML كملف Parquet خام
لتوضيح كيفية العمل مع ملف Parquet عشوائي بدلاً من إخفاء هذه
الخطوة في أداة ملائمة مثل sklearn.datasets.fetch_openml.
يمكن العثور على عنوان URL لملف Parquet في الوصف JSON لمجموعة بيانات طلب مشاركة الدراجات مع معرف 44063 على openml.org (https://openml.org/search?type=data&status=active&id=44063).
يتم توفير هاش sha256 للملف أيضًا لضمان سلامة الملف
الذي تم تنزيله.
from sklearn.model_selection import cross_validate
from sklearn.metrics import (
make_scorer,
mean_absolute_error,
mean_pinball_loss,
root_mean_squared_error,
)
from collections import defaultdict
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.model_selection import train_test_split
from sklearn.ensemble import HistGradientBoostingRegressor
import matplotlib.pyplot as plt
import polars.selectors as cs
import numpy as np
import polars as pl
from sklearn.datasets import fetch_file
pl.Config.set_fmt_str_lengths(20)
bike_sharing_data_file = fetch_file(
"https://openml1.win.tue.nl/datasets/0004/44063/dataset_44063.pq",
sha256="d120af76829af0d256338dc6dd4be5df4fd1f35bf3a283cab66a51c1c6abd06a",
)
bike_sharing_data_file
PosixPath('/root/scikit_learn_data/openml1.win.tue.nl/datasets_0004_44063/dataset_44063.pq')
نقوم بتحميل ملف Parquet باستخدام Polars للهندسة الميزات. يقوم Polars
تلقائيًا بتخزين التعبيرات الفرعية الشائعة التي يتم إعادة استخدامها في تعبيرات متعددة
(مثل pl.col("count").shift(1) أدناه). راجع
https://docs.pola.rs/user-guide/lazy/optimizations/ لمزيد من المعلومات.
df = pl.read_parquet(bike_sharing_data_file)
بعد ذلك، نلقي نظرة على الملخص الإحصائي لمجموعة البيانات حتى نتمكن من فهم البيانات التي نعمل عليها بشكل أفضل.
summary = df.select(cs.numeric()).describe()
summary
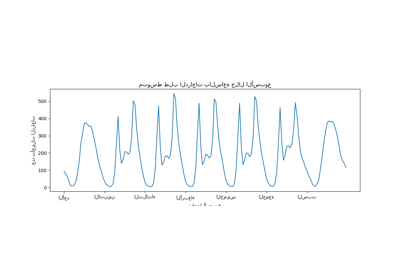
دعنا نلقي نظرة على عدد المواسم "fall"، "spring"، "summer"
و "winter" الموجودة في مجموعة البيانات للتأكد من أنها متوازنة.
df["season"].value_counts()
توليد الميزات المتأخرة المصممة بواسطة Polars#
دعنا نأخذ في الاعتبار مشكلة التنبؤ بالطلب في
الساعة التالية بناءً على الطلبات السابقة. نظرًا لأن الطلب هو متغير مستمر،
يمكن للمرء أن يستخدم بشكل حدسي أي نموذج انحدار. ومع ذلك، لا نملك
مجموعة البيانات المعتادة (X_train, y_train). بدلاً من ذلك، لدينا فقط
بيانات الطلب y_train منظمة تسلسليًا حسب الوقت.
lagged_df = df.select(
"count",
*[pl.col("count").shift(i).alias(f"lagged_count_{i}h") for i in [1, 2, 3]],
lagged_count_1d=pl.col("count").shift(24),
lagged_count_1d_1h=pl.col("count").shift(24 + 1),
lagged_count_7d=pl.col("count").shift(7 * 24),
lagged_count_7d_1h=pl.col("count").shift(7 * 24 + 1),
lagged_mean_24h=pl.col("count").shift(1).rolling_mean(24),
lagged_max_24h=pl.col("count").shift(1).rolling_max(24),
lagged_min_24h=pl.col("count").shift(1).rolling_min(24),
lagged_mean_7d=pl.col("count").shift(1).rolling_mean(7 * 24),
lagged_max_7d=pl.col("count").shift(1).rolling_max(7 * 24),
lagged_min_7d=pl.col("count").shift(1).rolling_min(7 * 24),
)
lagged_df.tail(10)
ولكن انتبه، فإن الأسطر الأولى لها قيم غير محددة لأن ماضيها غير معروف. يعتمد هذا على مقدار التأخير الذي استخدمناه:
lagged_df.head(10)
يمكننا الآن فصل الميزات المتأخرة في مصفوفة X ومتغير الهدف
(العددات التي يتعين التنبؤ بها) في مصفوفة من نفس البعد الأول y.
lagged_df = lagged_df.drop_nulls()
X = lagged_df.drop("count")
y = lagged_df["count"]
print("X shape: {}\ny shape: {}".format(X.shape, y.shape))
X shape: (17210, 13)
y shape: (17210,)
تقييم ساذج للتنبؤ بالطلب على الدراجات في الساعة التالية#
دعنا نقسم مجموعتنا المجدولة بشكل عشوائي لتدريب نموذج شجرة الانحدار المعزز (GBRT) وتقييمه باستخدام متوسط خطأ النسبة المئوية (MAPE). إذا كان نموذجنا يهدف إلى التنبؤ (أي التنبؤ ببيانات المستقبل من بيانات الماضي)، فيجب علينا عدم استخدام بيانات التدريب التي تكون لاحقة لبيانات الاختبار. في تعلم الآلة للسلاسل الزمنية لا يصح افتراض "i.i.d" (مستقل ومتطابق التوزيع) لأن نقاط البيانات ليست مستقلة ولها علاقة زمنية.
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
model = HistGradientBoostingRegressor().fit(X_train, y_train)
إلقاء نظرة على أداء النموذج.
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.3928958540837012
تقييم التنبؤ الصحيح للساعة التالية#
دعنا نستخدم استراتيجيات تقسيم التقييم الصحيحة التي تأخذ في الاعتبار البنية الزمنية لمجموعة البيانات لتقييم قدرة النموذج على التنبؤ بنقاط البيانات في المستقبل (لتجنب الغش عن طريق قراءة القيم من الميزات المتأخرة في مجموعة التدريب).
ts_cv = TimeSeriesSplit(
n_splits=3, # للحفاظ على سرعة الكمبيوتر المحمول بما يكفي على أجهزة الكمبيوتر المحمولة الشائعة
gap=48, # فجوة بيانات لمدة يومين بين التدريب والاختبار
max_train_size=10000, # الحفاظ على مجموعات التدريب بأحجام قابلة للمقارنة
test_size=3000, # للحصول على 2 أو 3 أرقام من الدقة في الدرجات
)
all_splits = list(ts_cv.split(X, y))
تدريب النموذج وتقييم أدائه بناءً على MAPE.
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
model = HistGradientBoostingRegressor().fit(X_train, y_train)
y_pred = model.predict(X_test)
mean_absolute_percentage_error(y_test, y_pred)
0.44300751539296973
خطأ التعميم المقاس عبر تقسيم الاختبار المدرب العشوائي هو متفائل للغاية. من المرجح أن يكون التعميم عبر تقسيم زمني أكثر تمثيلاً للأداء الحقيقي لنموذج الانحدار. دعنا نقيم هذه التباين في تقييم الخطأ لدينا مع تقسيم الصحيح:
cv_mape_scores = -cross_val_score(
model, X, y, cv=ts_cv, scoring="neg_mean_absolute_percentage_error"
)
cv_mape_scores
array([0.44300752, 0.27772182, 0.3697178 ])
التباين عبر التقسيمات كبير جدًا! في إعداد الحياة الواقعية يُنصح باستخدام المزيد من التقسيمات لتقييم التباين بشكل أفضل. دعنا نبلغ عن متوسط درجات CV وانحرافها المعياري من الآن فصاعدًا.
print(f"CV MAPE: {cv_mape_scores.mean():.3f} ± {cv_mape_scores.std():.3f}")
CV MAPE: 0.363 ± 0.068
يمكننا حساب العديد من مجموعات مقاييس التقييم ووظائف الخسارة، والتي يتم الإبلاغ عنها أدناه بقليل.
def consolidate_scores(cv_results, scores, metric):
if metric == "MAPE":
scores[metric].append(f"{value.mean():.2f} ± {value.std():.2f}")
else:
scores[metric].append(f"{value.mean():.1f} ± {value.std():.1f}")
return scores
scoring = {
"MAPE": make_scorer(mean_absolute_percentage_error),
"RMSE": make_scorer(root_mean_squared_error),
"MAE": make_scorer(mean_absolute_error),
"pinball_loss_05": make_scorer(mean_pinball_loss, alpha=0.05),
"pinball_loss_50": make_scorer(mean_pinball_loss, alpha=0.50),
"pinball_loss_95": make_scorer(mean_pinball_loss, alpha=0.95),
}
loss_functions = ["squared_error", "poisson", "absolute_error"]
scores = defaultdict(list)
for loss_func in loss_functions:
model = HistGradientBoostingRegressor(loss=loss_func)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["loss"].append(loss_func)
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
نمذجة عدم اليقين التنبؤي عبر الانحدار الكمي#
بدلاً من نمذجة القيمة المتوقعة لتوزيع \(Y|X\) مثلما تفعل خسائر المربعات الصغرى و Poisson، يمكن للمرء أن يحاول تقدير الكميات لتوزيع الشرطي.
\(Y|X=x_i\) من المتوقع أن تكون متغيرًا عشوائيًا لنقطة بيانات معينة \(x_i\) لأننا نتوقع أن عدد الإيجارات لا يمكن التنبؤ به بدقة 100% من الميزات. يمكن أن يتأثر بعوامل أخرى لا يتم التقاطها بشكل صحيح بواسطة الميزات المتأخرة الموجودة. على سبيل المثال، ما إذا كان سيمطر في الساعة التالية لا يمكن التنبؤ به بالكامل من بيانات إيجار الدراجات في الساعات السابقة. هذا ما نسميه عدم اليقين العشوائي.
يجعل الانحدار الكمي من الممكن إعطاء وصف أدق لهذا التوزيع دون افتراضات قوية حول شكله.
quantile_list = [0.05, 0.5, 0.95]
for quantile in quantile_list:
model = HistGradientBoostingRegressor(loss="quantile", quantile=quantile)
cv_results = cross_validate(
model,
X,
y,
cv=ts_cv,
scoring=scoring,
n_jobs=2,
)
time = cv_results["fit_time"]
scores["fit_time"].append(f"{time.mean():.2f} ± {time.std():.2f} s")
scores["loss"].append(f"quantile {int(quantile*100)}")
for key, value in cv_results.items():
if key.startswith("test_"):
metric = key.split("test_")[1]
scores = consolidate_scores(cv_results, scores, metric)
scores_df = pl.DataFrame(scores)
scores_df
دعنا نلقي نظرة على الخسائر التي تقلل من كل مقياس.
def min_arg(col):
col_split = pl.col(col).str.split(" ")
return pl.arg_sort_by(
col_split.list.get(0).cast(pl.Float64),
col_split.list.get(2).cast(pl.Float64),
).first()
scores_df.select(
pl.col("loss").get(min_arg(col_name)).alias(col_name)
for col_name in scores_df.columns
if col_name != "loss"
)
حتى إذا كانت توزيعات الدرجات تتداخل بسبب التباين في مجموعة البيانات،
فمن الصحيح أن متوسط RMSE أقل عندما loss="squared_error"، في حين أن
متوسط MAPE أقل عندما loss="absolute_error" كما هو متوقع. هذا هو
أيضًا الحال بالنسبة لمتوسط Pinball Loss مع الكميات 5 و95. الدرجات
المقابلة لخسارة الكمية 50 تتداخل مع الدرجات التي تم الحصول عليها
عن طريق تقليل وظائف الخسارة الأخرى، وهو أيضًا الحال بالنسبة لـ MAE.
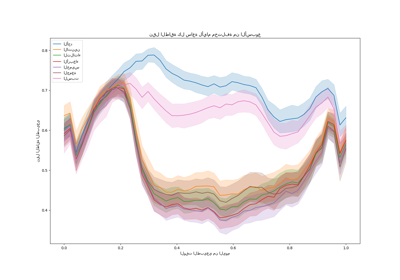
نظرة نوعية على التنبؤات#
يمكننا الآن تصور أداء النموذج فيما يتعلق بالخمسة بالمائة، والوسيط، والـ 95 بالمائة:
all_splits = list(ts_cv.split(X, y))
train_idx, test_idx = all_splits[0]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
X_train, X_test = X[train_idx, :], X[test_idx, :]
y_train, y_test = y[train_idx], y[test_idx]
max_iter = 50
gbrt_mean_poisson = HistGradientBoostingRegressor(
loss="poisson", max_iter=max_iter)
gbrt_mean_poisson.fit(X_train, y_train)
mean_predictions = gbrt_mean_poisson.predict(X_test)
gbrt_median = HistGradientBoostingRegressor(
loss="quantile", quantile=0.5, max_iter=max_iter
)
gbrt_median.fit(X_train, y_train)
median_predictions = gbrt_median.predict(X_test)
gbrt_percentile_5 = HistGradientBoostingRegressor(
loss="quantile", quantile=0.05, max_iter=max_iter
)
Total running time of the script: (0 minutes 12.648 seconds)
Related examples
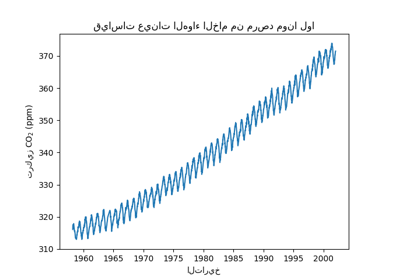
التنبؤ بمستوى ثاني أكسيد الكربون في مجموعة بيانات Mona Loa باستخدام انحدار العملية الغاوسية (GPR)