ملاحظة

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

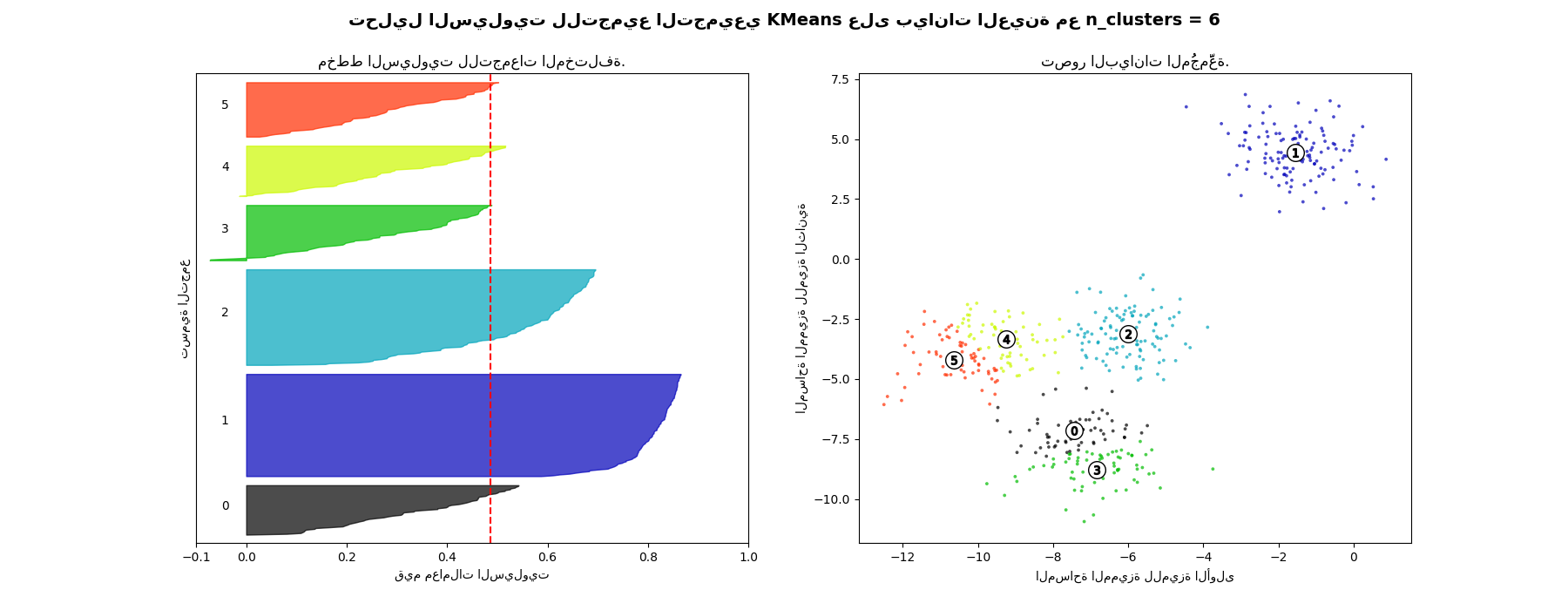
تحليل السيلويت لتحديد عدد التجمعات في التجميع التجميعي KMeans#

يمكن استخدام تحليل السيلويت لدراسة مسافة الفصل بين التجمعات الناتجة. يعرض مخطط السيلويت مقياسًا لمدى قرب كل نقطة في تجمع واحد من النقاط في التجمعات المجاورة، وبالتالي يوفر طريقة لتقييم المعلمات مثل عدد التجمعات بصريًا. يتراوح هذا المقياس بين [-1, 1].

تُشير معاملات السيلويت (كما يُشار إلى هذه القيم) بالقرب من +1 إلى أن العينة بعيدة عن التجمعات المجاورة. تشير القيمة 0 إلى أن العينة تقع على أو بالقرب من حد القرار بين تجمعين مجاورين، وتشير القيم السلبية إلى أن هذه العينات قد تكون مُنحت للتجمع الخاطئ.

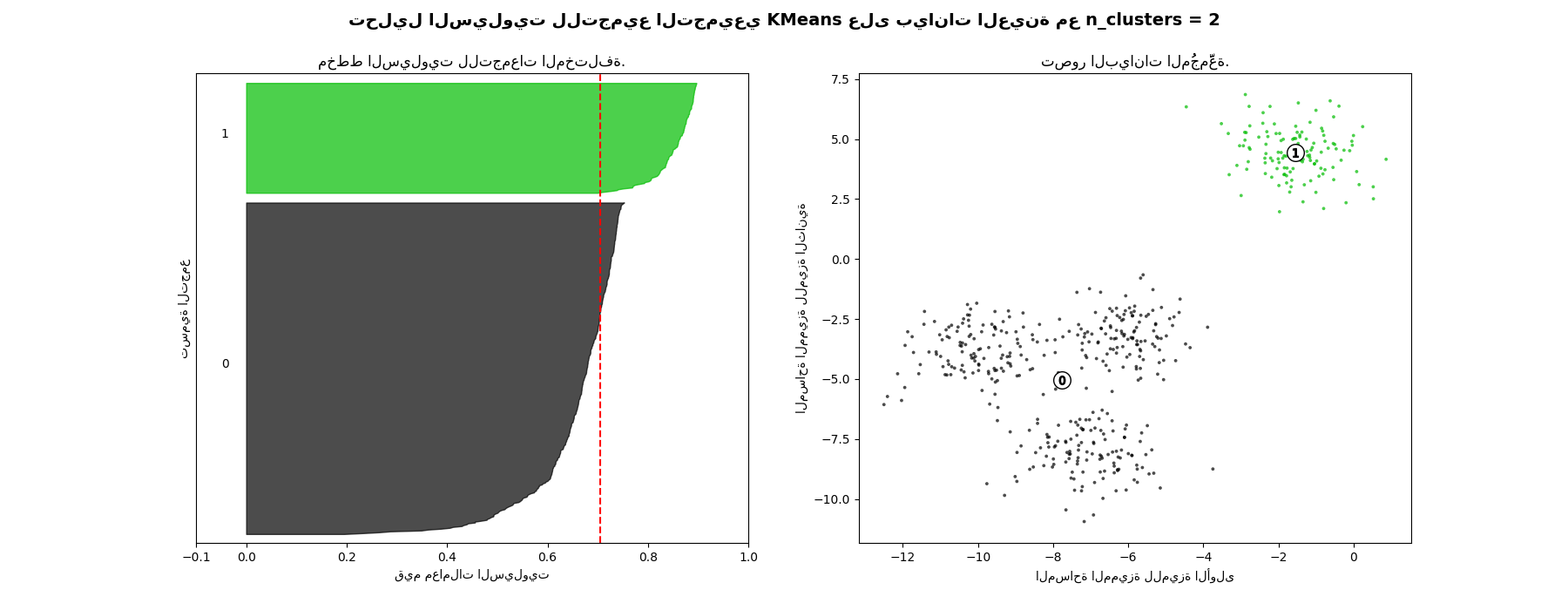
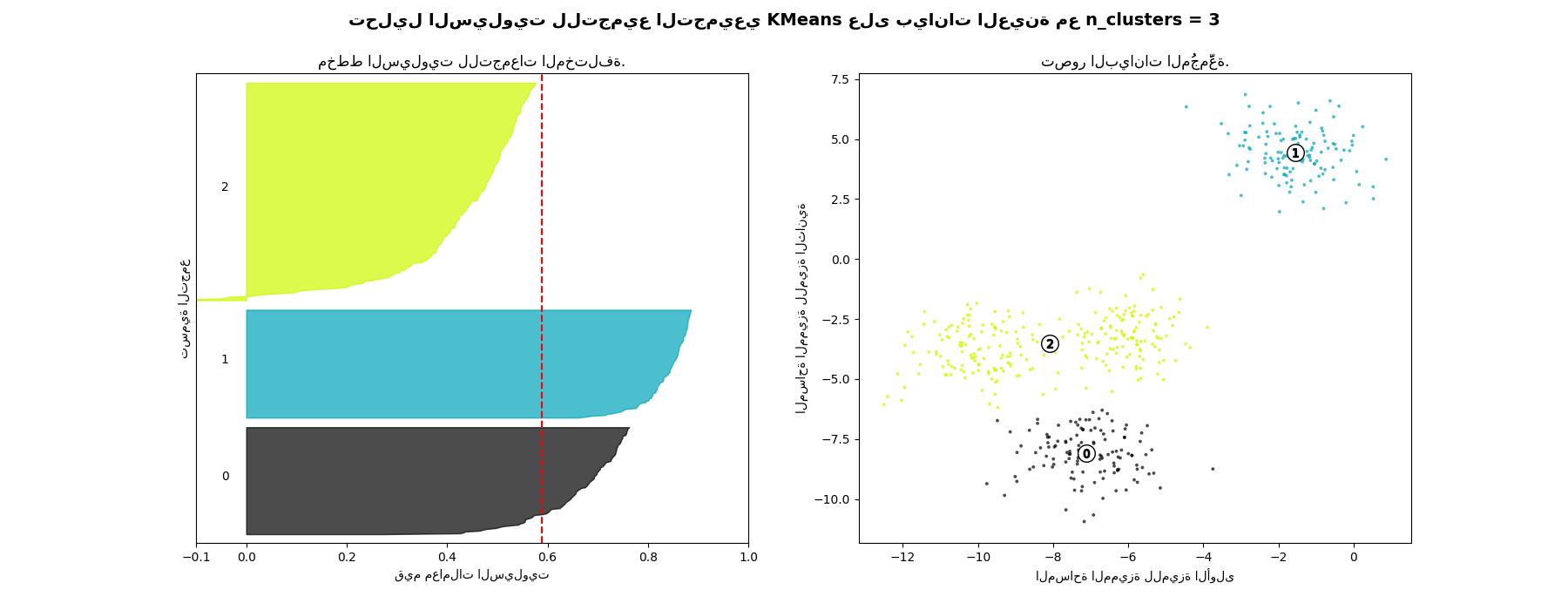
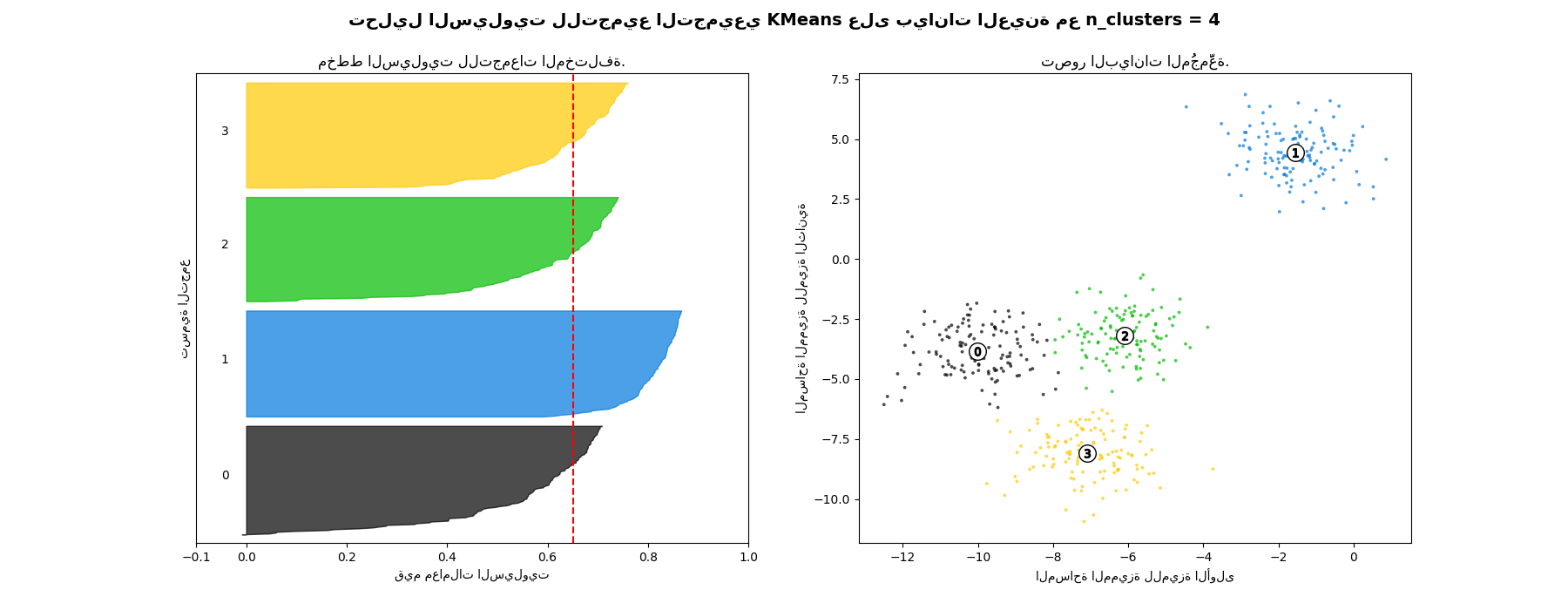
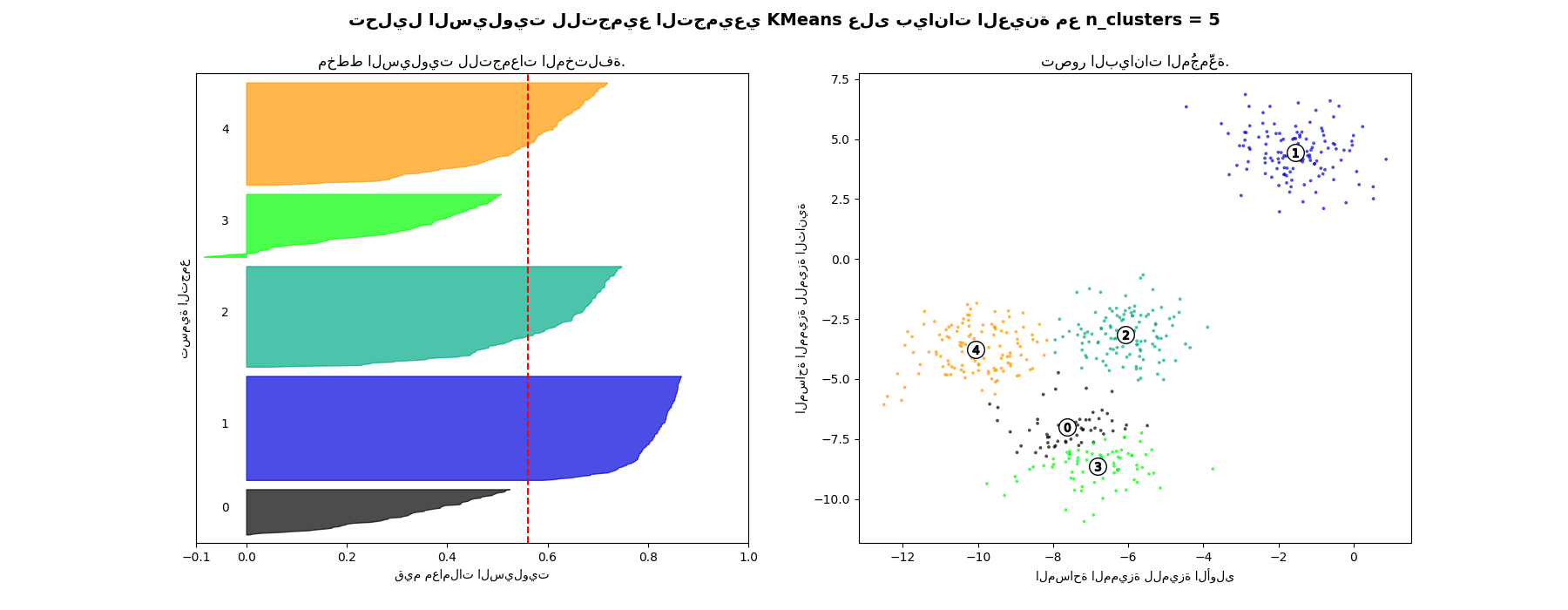
في هذا المثال، يُستخدم تحليل السيلويت لاختيار قيمة مثالية لـ "n_clusters". يُظهر مخطط السيلويت أن قيمة "n_clusters" تساوي 3 و5 و6 هي اختيار سيء للبيانات المُعطاة بسبب وجود تجمعات ذات درجات سيلويت أقل من المتوسط، وأيضًا بسبب التقلبات الواسعة في حجم مخططات السيلويت. يُظهر تحليل السيلويت ترددًا أكبر في الاختيار بين 2 و4.

أيضًا من سُمك مخطط السيلويت، يمكن تصور حجم التجمع. مخطط السيلويت للتجمع 0 عندما تكون "n_clusters" تساوي 2، أكبر في الحجم بسبب تجميع التجمعات الفرعية الثلاثة في تجمع واحد كبير. ومع ذلك، عندما تكون "n_clusters" تساوي 4، فإن جميع المخططات متشابهة تقريبًا في السُمك، وبالتالي فهي ذات أحجام متشابهة كما يمكن التحقق أيضًا من مخطط التبعثر المُعَلَّم على اليمين.

For n_clusters = 2 The average silhouette_score is : 0.7049787496083262
For n_clusters = 3 The average silhouette_score is : 0.5882004012129721
For n_clusters = 4 The average silhouette_score is : 0.6505186632729437
For n_clusters = 5 The average silhouette_score is : 0.561464362648773
For n_clusters = 6 The average silhouette_score is : 0.4857596147013469

# المؤلفون: مطوري scikit-learn
# معرف رخصة SPDX: BSD-3-Clause

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_samples, silhouette_score

# توليد بيانات العينة من make_blobs
# هذا الإعداد المحدد لديه تجمع واحد متميز و3 تجمعات موضوعة معًا.
X, y = make_blobs(
    n_samples=500,
    n_features=2,
    centers=4,
    cluster_std=1,
    center_box=(-10.0, 10.0),
    shuffle=True,
    random_state=1,
)  # من أجل إمكانية إعادة الإنتاج

range_n_clusters = [2, 3, 4, 5, 6]

for n_clusters in range_n_clusters:
    # إنشاء رسم فرعي مع 1 صف و2 أعمدة
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)

    # الرسم الفرعي الأول هو مخطط السيلويت
    # يمكن أن يتراوح معامل السيلويت من -1 إلى 1، ولكن في هذا المثال، يقع
    # جميعها ضمن النطاق [-0.1, 1]
    ax1.set_xlim([-0.1, 1])
    # (n_clusters+1)*10 لإدراج مساحة فارغة بين مخططات السيلويت
    # للتجمعات الفردية، لفصلها بوضوح.
    ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])

    # تهيئة المُجمِّع بقيمة n_clusters وبذرة مولد عشوائي
    # تساوي 10 من أجل إمكانية إعادة الإنتاج.
    clusterer = KMeans(n_clusters=n_clusters, random_state=10)
    cluster_labels = clusterer.fit_predict(X)

    # يُعطي silhouette_score متوسط القيمة لجميع العينات.
    # هذا يُقدم منظورًا حول كثافة وفصل التجمعات المُشكلة
    silhouette_avg = silhouette_score(X, cluster_labels)
    print(
        "For n_clusters =",
        n_clusters,
        "The average silhouette_score is :",
        silhouette_avg,
    )

    # حساب معاملات السيلويت لكل عينة
    sample_silhouette_values = silhouette_samples(X, cluster_labels)

    y_lower = 10
    for i in range(n_clusters):
        # تجميع معاملات السيلويت للعينات التي تنتمي إلى
        # التجمع i، وترتيبها
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]

        ith_cluster_silhouette_values.sort()

        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = cm.nipy_spectral(float(i) / n_clusters)
        ax1.fill_betweenx(
            np.arange(y_lower, y_upper),
            0,
            ith_cluster_silhouette_values,
            facecolor=color,
            edgecolor=color,
            alpha=0.7,
        )

        # وضع علامات على مخططات السيلويت بأرقام التجمعات في المنتصف
        ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # حساب y_lower الجديد للرسم التالي
        y_lower = y_upper + 10  # 10 للعينات 0

    ax1.set_title("مخطط السيلويت للتجمعات المختلفة.")
    ax1.set_xlabel("قيم معاملات السيلويت")
    ax1.set_ylabel("تسمية التجمع")

    # الخط العمودي لمعدل معامل السيلويت لجميع القيم
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

    ax1.set_yticks([])  # مسح تسميات/علامات المحور y
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    # الرسم الثاني يُظهر التجمعات المُشكلة بالفعل
    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(
        X[:, 0], X[:, 1], marker=".", s=30, lw=0, alpha=0.7, c=colors, edgecolor="k"
    )

    # وضع علامات على التجمعات
    centers = clusterer.cluster_centers_
    # رسم دوائر بيضاء في مراكز التجمعات
    ax2.scatter(
        centers[:, 0],
        centers[:, 1],
        marker="o",
        c="white",
        alpha=1,
        s=200,
        edgecolor="k",
    )

    for i, c in enumerate(centers):
        ax2.scatter(c[0], c[1], marker="$%d$" % i, alpha=1, s=50, edgecolor="k")

    ax2.set_title("تصور البيانات المُجمَّعة.")
    ax2.set_xlabel("المساحة المميزة للميزة الأولى")
    ax2.set_ylabel("المساحة المميزة للميزة الثانية")

    plt.suptitle(
        "تحليل السيلويت للتجميع التجميعي KMeans على بيانات العينة مع n_clusters = %d"
        % n_clusters,
        fontsize=14,
        fontweight="bold",
    )

plt.show()